7.4 The extended Cox-Ingersoll-Ross model
7.4 The extended Cox-Ingersoll-Ross model
Setting ² = ½ in (7.2) leads to the extension of the CIR model proposed by HW:
The assumption is made that the market price of interest rate risk has the functional form » ( t ) ˆ r where » ( t ) is some function bounded on any time interval (0, ). Again, let P be the price of a zero coupon bond and make use of Ito's Lemma to derive its price process:
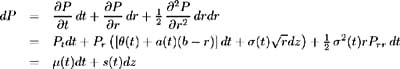
where ¼ ( ·) and s ( ·) are the drift and volatility of P defined as:
Letting m ( t )= » ( t ) ˆ r be the market price of interest rate risk, we have ¼ ( t ) ˆ’ rP = m ( t ) s ( t ) and so:
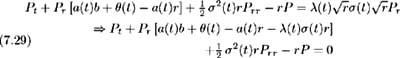
Let
and (7.29) may be expressed as:
As in (7.18), the price of the zero coupon bond is assumed to have the functional form:
Hence (7.30) becomes:
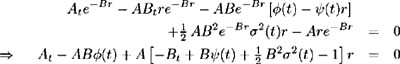
To solve this partial differential equation we must solve the system of differential equations:
subject to the boundary conditions A ( T, T )= 1 and B ( T, T ) = 0. In the special case where ( t ), ˆ ( t ) and ƒ ( t ) are constant, we solve (7.31a) and (7.31b) to give analytical formulae for A ( t, T ) and B ( t, T ) as presented in the original CIR paper [5] [ 18 ]:
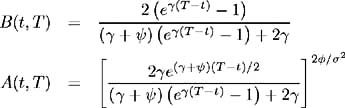
where ![]() . In the HW extension of this model, ƒ ( t ) needs to be chosen to reflect the observed current and future volatilities of the short- term interest rate. As in the case of the extended Vasicek model, we use:
. In the HW extension of this model, ƒ ( t ) needs to be chosen to reflect the observed current and future volatilities of the short- term interest rate. As in the case of the extended Vasicek model, we use:
-
ƒ (0), the current i.e. time 0 volatility of the short-term interest rate,
-
current interest rate term structure,
-
current volatility term structure.
to determine A (0, T ) and B (0, T ). These initial conditions, together with the already specified boundary conditions allow us to solve equations (7.31a) and (7.31b).
Firstly, differentiating (7.31b) with respect to T , and multiplying by B yields:
Multiplying (7.31b) by B T and subtracting (7.32) gives:
Since this equation cannot be solved analytically, B ( t, T ) must be obtained via a numerical method such as finite differences. ƒ ( t ) is a known function obtained from the current and future short-term interest rate volatilities observed in the market. Hence, once B ( t, T ) is known, equation (7.31b) may be used to determine ˆ ( t ).
Next, solve (7.31a) for A ( t, T ). From (7.31a) we have:
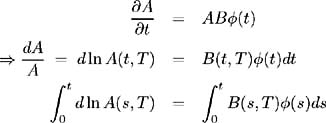
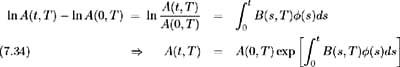
To be able to fully evaluate A ( t, T ), ( ·) must be known. Since A ( T, T )=1 and A (0, T ) is known, evaluate (7.34) at t = T :

which may be used to determine ( ·) iteratively. This is computationally time-consuming since ( s ) needs to be evaluated at each time point in the interval [0, t ] so that the integral in (7.34) may be calculated numerically .
[5] These are the same formulae as calculated for the CIR model in Chapter 2 equations (2.36) and (2.38) with the following notational substitutions: = and ˆ = + » .
EAN: 2147483647
Pages: 132