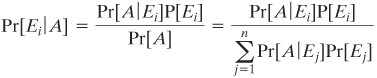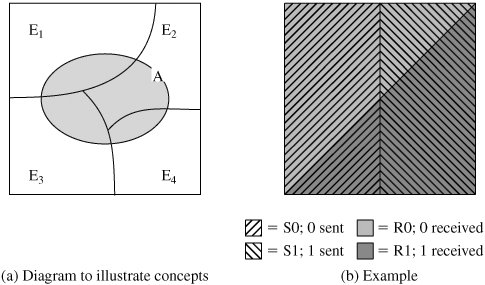
Appendix 18A The Base-Rate Fallacy | Cryptography and Network Security (4th Edition)

[Page 594 (continued)]

We begin with a review of important results from probability theory, then demonstrate the base-rate fallacy.

Conditional Probability and Independence

We often want to know a probability that is conditional on some event. The effect of the condition is to remove some of the outcomes from the sample space. For example, what is the probability of getting a sum of 8 on the roll of two dice, if we know that the face of at least one die is an even number? We can reason as follows. Because one die is even and the sum is even, the second die must show an even number. Thus, there are three equally likely successful outcomes: (2, 6), (4, 4) and (6, 2), out of a total set of possibilities of [36 - (number of events with both faces odd)] = 36 - 3 x 3 = 27. The resulting probability is 3/27 = 1/9.

Formally, the conditional probability of an event A assuming the event B has occurred, denoted by Pr[A|B]is defined as the ratio

where we assume Pr[B] is not zero.

In our example, A = {sum of 8} and B = {at least one die even}. The quantity Pr[AB] encompasses all of those outcomes in which the sum is 8 and at least one die is even. As we have seen, there are three such outcomes. Thus, Pr[AB] = 3/36 = 1/12. A moment's thought should convince you that Pr[B] = 3/4. We can now calculate

[Page 595]

This agrees with our previous reasoning.

Two events A and B are called independent if Pr[AB] = Pr[A]Pr[B]. It can easily be seen that if A and B are independent, Pr[A|B] = Pr[A] and Pr[B|A] = Pr[B].

Bayes' Theorem

One of the most important results from probability theory is known as Bayes' theorem. First we need to state the total probability formula. Given a set of mutually exclusive events E₁, E₂,... E_n such that the union of these events covers all possible outcomes, and given an arbitrary event A, then it can be shown that

Equation 18-1

Bayes' theorem may be stated as follows:

Equation 18-2

Figure 18.7a illustrates the concepts of total probability and Bayes' theorem.

Figure 18.7. Illustration of Total Probability and Bayes' Theorem

Bayes' theorem is used to calculate "posterior odds," that is, the probability that something really is the case, given evidence in favor of it. For example, suppose we are transmitting a sequence of zeroes and ones over a noisy transmission line. Let S0 and S1 be the events a zero is sent at a given time and a one is sent, respectively, and R0 and R1 be the events that a zero is received and a one is received. Suppose we know the probabilities of the source, namely Pr[S1] = p and Pr[S0] = 1 p. Now the line is observed to determine how frequently an error occurs when a one is sent and when a zero is sent, and the following probabilities are calculated: Pr[R0|S1] = p_a and Pr[R1|S0] = p_b. If a zero is received, we can then calculate the conditional probability of an error, namely the conditional probability that a one was sent given that a zero was received, using Bayes' theorem:

[Page 596]

Figure 18.7b illustrates the preceding equation. In the figure, the sample space is represented by a unit square. Half of the square corresponds to S0 and half to S1, so Pr[S0] = Pr[S1] = 0.5. Similarly, half of the square corresponds to R0 and half to R1, so Pr[R0] = Pr[R1] = 0.5. Within the area representing S0, 1/4 of that area corresponds to R1, so Pr[R1/S0] = 0.25. Other conditional probabilities are similarly evident.

The Base-Rate Fallacy Demonstrated

Consider the following situation. A patient has a test for some disease that comes back positive (indicating he has the disease). You are told that

The accuracy of the test is 87% (i.e., if a patient has the disease, 87% of the time, the test yields the correct result, and if the patient does not have the disease, 87% of the time, the test yields the correct result).
The incidence of the disease in the population is 1%.

Given that the test is positive, how probable is it that the patient does not have the disease? That is, what is the probability that this is a false alarm? We need Bayes' theorem to get the correct answer:

Thus, in the vast majority of cases, when a disease condition is detected, it is a false alarm.

This problem, used in a study [PIAT91], was presented to a number of people. Most subjects gave the answer 13%. The vast majority, including many physicians, gave a number below 50%. Many physicians who guessed wrong lamented, "If you are right, there is no point in making clinical tests!" The reason most people get it wrong is that they do not take into account the basic rate of incidence (the base rate) when intuitively solving the problem. This error is known as the base-rate fallacy.

How could this problem be fixed? Suppose we could drive both of the correct result rates to 99.9%. That is, suppose we have Pr[positive/disease] = 0.999 and Pr[negative/well] = 0.999. Plugging these numbers into the Equation (18.2), we get Pr[well/positive] = 0.09. Thus, if we can accurately detect disease and accurately detect lack of disease at a level of 99.9%, then the rate of false alarms will be 9%. This is much better, but still not ideal. Moreover, again assume 99.9% accuracy, but now suppose that the incidence of the disease in the population is only 1/10000 = 0.0001. We then end up with a rate of false alarms of 91%. In actual situations, [AXEL00] found that the probabilities associated with intrusion detection systems were such that the false alarm rate was unsatisfactory.

[Page 597]