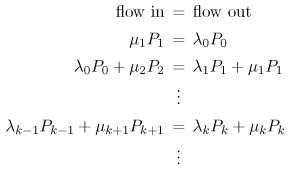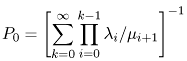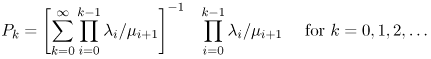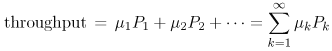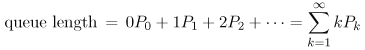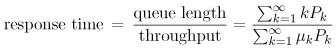10.8 Generalized Birth-Death Models
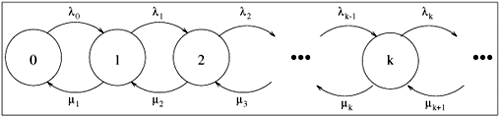
| A class of Markov models, called birth-death models, is quite useful and exhibits a general solution. Given that the system is in a particular state k, indicating k customers in the system, one of two events can occur that can cause the system to leave state k. Either a birth occurs, where the arrival of another customer causes the system to enter state k + 1, or a death occurs, where the departure of a customer causes the system to enter state k 1. Given that the current state is state k, assume that the arrival rate (i.e., the birth rate) of new customers is lk and that the completion rate (i.e., the death rate) of customers is mk. That is, the birth and death rates are state-dependent. See the state transition diagram of Fig. 10.6. Figure 10.6. Generalized birth-death state-space diagram. Following the solution approach of the previous sections, the system of flow balance equations is After some algebraic manipulation and using the conservation of total probability, P0 + P1 + P2 + ··· = 1, the solution is obtained as Equation 10.8.1 where the first term in the summation is defined to be 1. Therefore, the generalized steady-state solution, for any birth-death system, for being in any particular state k is: Equation 10.8.2 From this generalized steady-state solution, obtaining expressions for other performance measures is straightforward: Equation 10.8.3 Equation 10.8.4 Equation 10.8.5 Equation 10.8.6 |
EAN: 2147483647
Pages: 166