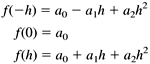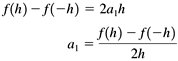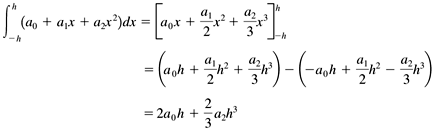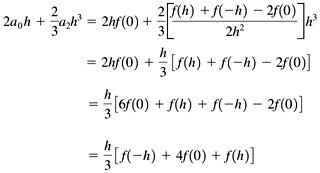7.3 Simpson s Algorithm

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  7.   Numerical Integration

---

7.3 Simpson's Algorithm

Just as trapezoids fit better under a curve than rectangles do, parabolas fit even better than trapezoids. This is the basis for Simpson's algorithm, ^[3] which can extend beyond parabolas (second-degree polynomials) to higher degree polynomials . Figure 7-3 shows how to use parabolic regions (their tops are parabolas) to estimate the area under a curve.

^[3] Also known as Simpson's rule. Thomas Simpson (1710 §C1761) was a self-taught mathematician who developed this algorithm in 1743.

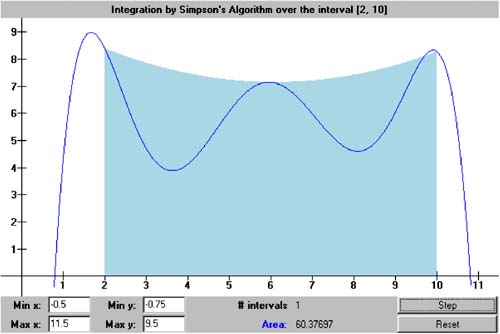
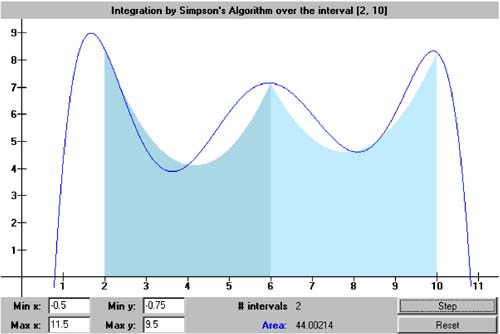
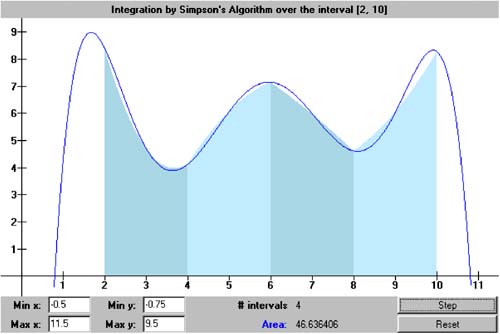
Figure 7-3. Using parabolic regions to estimate the area under a curve defined by a function f ( x ).

We need to derive the formula for the area of a single parabolic region. From Chapter 6, we know that we can define a unique parabola with three points. Let h be the common width of each region, and we'll define the parabola over two adjacent regions. Since it doesn't matter where along the x axis the parabolic region lies, it is computationally convenient to set the x values of the three points to - h, 0, and h.

The power form of a parabolic function is f ( x ) = a + a ₁ x + a ₂ x ² . That gives us

Subtract the first equation from the third:

Add the first and third equations and substitute the value of a :

The integral of a second-degree polynomial is something we can compute analytically:

Now substitute the values for a and a ₂ :

Let the x values of three points of the parabola be x ₁ , x ₂ , and x ₃ , where x ₁ = - h, x ₂ = 0, and x ₃ = h. Then the area of the parabolic region is

Class SimpsonsIntegrator in package numbercruncher.mathutils implements Simpson's integration algorithm with parabolas. See Listing 7-1d.

Listing 7-1d The class that implements Simpson's integration algorithm with parabolas.

 package numbercruncher.mathutils; /**  * Function integrator that implements  * Simpson's algorithm with parabolas.  */ public class SimpsonsIntegrator implements Integrator {     /** the function to integrate */  private Evaluatable integrand;     /**      * Constructor.      * @param integrand the function to integrate      */     public SimpsonsIntegrator(Evaluatable integrand)     {         this.integrand = integrand;     }     /**      * Integrate the function from a to b using Simpson's algorithm,      * and return an approximation to the area.      * (Integrator implementation.)      * @param a the lower limit      * @param b the upper limit      * @param intervals the number of equal-width intervals      * @return an approximation to the area      */     public float integrate(float a, float b, int intervals)     {         if (b <= a) return 0;         float h         = (b - a)/intervals/2;  // interval width                                                 //   (split in two)         float totalArea = 0;         // Compute the area using the current number of intervals.         for (int i = 0; i < intervals; ++i) {             float x1 = a + 2*i*h;             totalArea += areaOf(x1, h);         }         return totalArea;     }     /**      * Compute the area of the ith parabolic region.      * @param x1 the left bound of the region      * @param h the interval width      * @return the area of the region      */     private float areaOf(float x1, float h)     {         float x2   = x1 + h;               // middle         float x3   = x2 + h;               // right bound of the region         float y1   = integrand.at(x1);     // value at left bound         float y2   = integrand.at(x2);     // value at the middle         float y3   = integrand.at(x3);     // value at right bound         float area = h*(y1 + 4*y2+ y3)/3;  // area of the region         return area;     } } 

Like the constructor for class TrapezoidalIntegrator we saw earlier, the constructor for class SimpsonsIntegrator takes an Evaluatable argument and the number of intervals. Method integrate() performs the integration and returns an approximation to the area.

Instead of working with pairs of adjacent regions, method integrate() splits each region in half, so that method areaOf() has three points to work with. This latter method implements the formula for the area of a parabolic region.

If we give the noninteractive version of Program 7 §C1 the command-line argument "simpsons," it instantiates a SimpsonsIntegrator object to compute the approximate value of p . See the output in Listing 7-1e.

Simpson's integration algorithm converges faster than the trapezoidal integration algorithm. But the computation of each region's area is a bit more complicated, and so there is more opportunity for roundoff errors. In this example, the errors prevent the estimate for p to be more accurate than that from the trapezoidal integration algorithm.

Listing 7-1e The output of the noninteractive version of Program 7 §C1, which computes an approximation to the value of p with Simpson's integration algorithm when given the command-line argument "simpsons."

Output:

 ALGORITHM: Simpson's     n             pi        % Error - - - - - - - - - - - - - - - - - -     1      2.9760678      5.2688203     2      3.0835953      1.8461139     4       3.121189      0.6494647     8      3.1343977     0.22902104    16      3.1390526     0.08085148    32       3.140695    0.028570175    64      3.1412754    0.010098308   128      3.1414802    0.003579272   256      3.1415539   0.0012342404   512      3.1415799    4.070286E-4  1024      3.1415892  1.11053734E-4  2048      3.1415887   1.2623193E-4 

Screen 7-1b shows screen shots of the first three iterations of the interactive version of Program 7 §C1 using Simpson's algorithm.

Screen 7-1b. The first three iterations of the interactive version of Program 7 §C1 using Simpson's algorithm.

---

Top