Don t Curse: Be Recursive
Don’t Curse: Be Recursive
Cursing is bad, as your mother may have told you, but being recursive can be good—very, very good! A recursive function is one that calls itself.
Our example of a recursive function will be one that calculates numbers in the Fibonacci series.
The Fibonacci series is named after Leonard Pisano, a mathematician who lived in the 1200s and, for some reason, called himself Fibonacci. This series of numbers is calculated by starting with zero and one, adding them, and then adding the two previous numbers to obtain the next number. In other words, the Nth number in the Fibonacci series equals the Nth – 1 number plus the Nth – 2 number.
As you’ll see, using this formula, the Nth number of the Fibonacci series can easily be calculated using a recursive function—one that calls itself to determine the Nth – 1 and the Nth – 2 Fibonacci numbers.
By the way, the Fibonacci series is famous because it often occurs in natural phenomena such as spiraling plants, chambered nautilus shells, and so on. Fibonacci first discovered these numbers during a calculation of how many rabbits could be eventually expected when starting out with one mating pair.
“A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair, which from the second month on becomes productive?” asked the mathematician Fibonacci, writing in 1202 in his book Liber Abaci (“Book of the Abacus”), describing the rabbit reproduction problem that gave rise to the Fibonacci series.
To answer the rabbit problem, imagine that there are XN pairs of rabbits after N months. To find out how many pairs of rabbits there will be in the next month, month N + 1, you’d start with XN and add the new pairs of rabbit born in the month. (This, of course, assumes that rabbits are immortal and never die—a true Malthusian nightmare.)
As the problem is defined, new pairs of rabbits are only born to rabbits at least one month old. So, the number of new pairs is XN - 1.
This means that the number of rabbit pairs in the N + 1 month can be calculated as XN+1 = XN + XN-1, which is the same thing as the Fibonacci series I just described.
Coming down from planet rabbit to planet earth, let’s see how we can use a recursive function (one that calls itself) to generate the Fibonacci series of numbers. To see how to do this, let’s have a look at the first few numbers in the series, starting with the first, or zero, Fibonacci number, as shown in Table 5-1.
| Number in Fibonacci Series | Value |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
Here’s how to declare a function (named fib) that calculates the Nth number in the Fibonacci series:
function fib (inNum) { } The argument inNum in this function declaration represents the number in the series, and the return value of the fib function will be the Fibonacci series value for the number in the series.
The first thing to do within the fib function is to set up an if statement that provides values for the first two Fibonacci numbers (fib(0) and fib(1)). (Chapter 3, “ Using Conditional Statements,” explained if statements.) Here’s the if statement:
if (inNum == 0) var fibNum = 0; else { if (inNum == 1) fibNum = 1; else { } } So far, this if statement uses the comparison operator (= =) to check to see if the Fibonacci number is the zero element in the series, and, if it’s the zero element, assigns the value 0 to the variable fibNum. (The variable fibNum will be used to store the value of the Fibonacci number and returned as the value of the fib function.)
| Note | In JavaScript, the comparison operator (= =) checks to see if two values are the same. Comparison isn’t to be confused with assignment, which assigns a value to a variable. The assignment operator is a single equals sign (=). In some languages, such as Visual Basic, comparison and assignment are both represented by the same symbol, usually a single equals sign. |
Next, the if statement uses the comparison operator to check to see if the Fibonacci number is the next element in the series, fib(1):
if (inNum == 1) fibNum = 1; else { } If it’s fib(1), then the value 1 is assigned to fibNum. If not, it’s time to make rabbits! Here’s where the recursive function call, which—rabbits or no rabbits—is truly a sexy thing, comes in:
if (inNum == 1) fibNum = 1; else { // recursive function call fibNum = fib(inNum - 2) + fib(inNum - 1); } Essentially, this looks just like the definition of the series. Any given Fibonacci number, after the first two, is calculated recursively as the sum of the two numbers that came before it in the series.
| Tip | Recursive algorithms, such as this one, are great for simplicity and clarity, but they may result in programs that are computationally slow. Can you come up with a nonrecursive, faster way to calculate the numbers in the Fibonacci series? |
All that remains is the return of the Fibonacci value. Figure 5-6 shows this, along with the complete recursive Fibonacci function.
Listing 5.6: Calculating a Fibonacci Number Recursively
function fib (inNum) { if (inNum == 0) var fibNum = 0; else { if (inNum == 1) fibNum = 1; else { // recursive function call fibNum = fib(inNum - 2 ) + fib(inNum - 1); } } return fibNum; } | Try This at Home | Now that we know how to calculate a single Fibonacci number (by passing to the fib function shown in Listing 5-6 the number in the series we’d like to calculate), let’s add code that shows all the Fibonacci numbers up to a specified maximum in the series. |
| Tip | You don’t want to attempt to calculate a number too far along in the series. Anything greater than the twenty-fifth number in the series is likely to take a long time to calculate recursively and may cause your Web browser to abort the process. |
The following is another function, writeFibs, that uses a for loop to obtain each number in the Fibonacci series by calling the original fib function, up to a maximum series number supplied as input to the function:
function writeFibs(topFib) { for (var i=0; i <= topFib ; i++) { document.write ("Fib(" + i + ") = " + fib(i) + " rabbit pairs<br>"); } } Each Fibonacci number obtained is displayed on its own line, along with the phrase “rabbit pairs” (just for fun!).
Listing 5-7 shows the two functions (fib and writeFibs) in an HTML page along with an HTML form for the user to enter the number of Fibonacci numbers to calculate. If you open the HTML page shown in Listing 5-7 in a Web browser, it’ll look like Figure 5-7.
Listing 5.7: Counting Rabbits (Calculating the Fibonacci Series Using a Recursive Function)
<HTML> <HEAD> <TITLE> Counting rabbits... </TITLE> <SCRIPT> function fib (inNum) { if (inNum == 0) var fibNum = 0; else { if (inNum == 1) fibNum = 1; else { // recursive function call fibNum = fib(inNum - 2) + fib(inNum - 1); } } return fibNum; } function writeFibs(topFib) { for (var i=0; i <= topFib ; i++) { document.write ("Fib(" + i + ") = " + fib(i) + " rabbit pairs<br>"); } } </SCRIPT> </HEAD> <BODY> <FORM Name="theForm"> <TABLE cellspacing=5> <TR> <TD> <INPUT Type=Text Name="numFibs"> <TD> <INPUT Type=Button Value="Show Fibs" onClick='writeFibs(numFibs.value);'> </TR> </TABLE> </FORM> </BODY> </HTML> 
Figure 5-7: The user enters the number of Fibonacci numbers to display.
Enter a number and click Show Fibs. The numbers in the Fibonacci series will be displayed (see Figure 5-8).
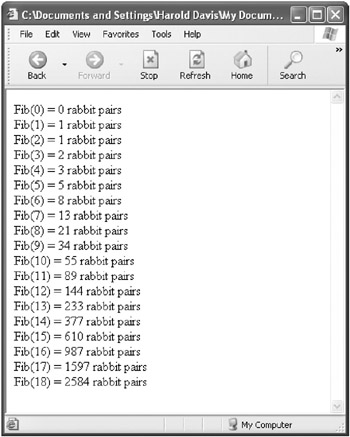
Figure 5-8: By the eighteenth generation, there starts to be plenty of rabbits!
| Caution | The program shown in Listing 5-7 works in Internet Explorer, but not in Navigator or Mozilla. |
EAN: 2147483647
Pages: 115