Examples
Example 42.1. Stepwise Logistic Regression and Predicted Values
Consider a study on cancer remission (Lee 1974). The data, consisting of patient characteristics and whether or not cancer remission occurred, are saved in the data set Remission .
data Remission; input remiss cell smear infil li blast temp; label remiss=Complete Remission; datalines; 1 .8 .83 .66 1.9 1.1 .996 1 .9 .36 .32 1.4 .74 .992 0 .8 .88 .7 .8 .176 .982 0 1 .87 .87 .7 1.053 .986 1 .9 .75 .68 1.3 .519 .98 0 1 .65 .65 .6 .519 .982 1 .95 .97 .92 1 1.23 .992 0 .95 .87 .83 1.9 1.354 1.02 0 1 .45 .45 .8 .322 .999 0 .95 .36 .34 .5 0 1.038 0 .85 .39 .33 .7 .279 .988 0 .7 .76 .53 1.2 .146 .982 0 .8 .46 .37 .4 .38 1.006 0 .2 .39 .08 .8 .114 .99 0 1 .9 .9 1.1 1.037 .99 1 1 .84 .84 1.9 2.064 1.02 0 .65 .42 .27 .5 .114 1.014 0 1 .75 .75 1 1.322 1.004 0 .5 .44 .22 .6 .114 .99 1 1 .63 .63 1.1 1.072 .986 0 1 .33 .33 .4 .176 1.01 0 .9 .93 .84 .6 1.591 1.02 1 1 .58 .58 1 .531 1.002 0 .95 .32 .3 1.6 .886 .988 1 1 .6 .6 1.7 .964 .99 1 1 .69 .69 .9 .398 .986 0 1 .73 .73 .7 .398 .986 ;
The data set Remission contains seven variables . The variable remiss is the cancer remission indicator variable with a value of 1 for remission and a value of 0 for nonremission. The other six variables are the risk factors thought to be related to cancer remission.
The following invocation of PROC LOGISTIC illustrates the use of stepwise selection to identify the prognostic factors for cancer remission. A significance level of 0.3 (SLENTRY=0.3) is required to allow a variable into the model, and a significance level of 0.35 (SLSTAY=0.35) is required for a variable to stay in the model. A detailed account of the variable selection process is requested by specifying the DETAILS option. The Hosmer and Lemeshow goodness-of-fit test for the final selected model is requested by specifying the LACKFIT option. The OUTEST= and COVOUT options in the PROC LOGISTIC statement create a data set that contains parameter estimates and their covariances for the final selected model. The response variable option EVENT= sets remiss =1 (remission) to be Ordered Value 1 so that the probability of remission is modeled . The OUTPUT statement creates a data set that contains the cumulative predicted probabilities and the corresponding confidence limits, and the individual and cross validated predicted probabilities for each observation.
title Stepwise Regression on Cancer Remission Data; proc logistic data=Remission outest=betas covout; model remiss(event=1)=cell smear infil li blast temp / selection=stepwise slentry=0.3 slstay=0.35 details lackfit; output out=pred p=phat lower=lcl upper=ucl predprob=(individual crossvalidate); run; proc print data=betas; title2 Parameter Estimates and Covariance Matrix; run; proc print data=pred; title2 Predicted Probabilities and 95% Confidence Limits; run;
In stepwise selection, an attempt is made to remove any insignificant variables from the model before adding a significant variable to the model. Each addition or deletion of a variable to or from a model is listed as a separate step in the displayed output, and at each step a new model is fitted. Details of the model selection steps are shown in Output 42.1.1 “Output 42.1.5.
| |
Stepwise Regression on Cancer Remission Data The LOGISTIC Procedure Model Information Data Set WORK.REMISSION Response Variable remiss Complete Remission Number of Response Levels 2 Model binary logit Optimization Technique Fishers scoring Number of Observations Read 27 Number of Observations Used 27 Response Profile Ordered Total Value remiss Frequency 1 0 18 2 1 9 Probability modeled is remiss=1. Stepwise Selection Procedure Step 0. Intercept entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.6931 0.4082 2.8827 0.0895 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 9.4609 6 0.1493 Analysis of Effects Eligible for Entry Score Effect DF Chi-Square Pr > ChiSq cell 1 1.8893 0.1693 smear 1 1.0745 0.2999 infil 1 1.8817 0.1701 li 1 7.9311 0.0049 blast 1 3.5258 0.0604 temp 1 0.6591 0.4169
| |
| |
Step 1. Effect li entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 36.372 30.073 SC 37.668 32.665 -2 Log L 34.372 26.073 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 8.2988 1 0.0040 Score 7.9311 1 0.0049 Wald 5.9594 1 0.0146 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -3.7771 1.3786 7.5064 0.0061 li 1 2.8973 1.1868 5.9594 0.0146 Association of Predicted Probabilities and Observed Responses Percent Concordant 84.0 Somers D 0.710 Percent Discordant 13.0 Gamma 0.732 Percent Tied 3.1 Tau-a 0.328 Pairs 162 c 0.855 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 3.1174 5 0.6819 NOTE: No effects for the model in Step 1 are removed. Analysis of Effects Eligible for Entry Score Effect DF Chi-Square Pr > ChiSq cell 1 1.1183 0.2903 smear 1 0.1369 0.7114 infil 1 0.5715 0.4497 blast 1 0.0932 0.7601 temp 1 1.2591 0.2618
| |
| |
Step 2. Effect temp entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 36.372 30.648 SC 37.668 34.535 -2 Log L 34.372 24.648 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 9.7239 2 0.0077 Score 8.3648 2 0.0153 Wald 5.9052 2 0.0522 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 47.8448 46.4381 1.0615 0.3029 li 1 3.3017 1.3593 5.9002 0.0151 temp 1 -52.4214 47.4897 1.2185 0.2697 Association of Predicted Probabilities and Observed Responses Percent Concordant 87.0 Somers D 0.747 Percent Discordant 12.3 Gamma 0.752 Percent Tied 0.6 Tau-a 0.345 Pairs 162 c 0.873 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 2.1429 4 0.7095 NOTE: No effects for the model in Step 2 are removed. Analysis of Effects Eligible for Entry Score Effect DF Chi-Square Pr > ChiSq cell 1 1.4700 0.2254 smear 1 0.1730 0.6775 infil 1 0.8274 0.3630 blast 1 1.1013 0.2940
| |
| |
Step 3. Effect cell entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 36.372 29.953 SC 37.668 35.137 -2 Log L 34.372 21.953 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 12.4184 3 0.0061 Score 9.2502 3 0.0261 Wald 4.8281 3 0.1848 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 67.6339 56.8875 1.4135 0.2345 cell 1 9.6521 7.7511 1.5507 0.2130 li 1 3.8671 1.7783 4.7290 0.0297 temp 1 -82.0737 61.7124 1.7687 0.1835 Association of Predicted Probabilities and Observed Responses Percent Concordant 88.9 Somers D 0.778 Percent Discordant 11.1 Gamma 0.778 Percent Tied 0.0 Tau-a 0.359 Pairs 162 c 0.889 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 0.1831 3 0.9803 NOTE: No effects for the model in Step 3 are removed. Analysis of Effects Eligible for Entry Score Effect DF Chi-Square Pr > ChiSq smear 1 0.0956 0.7572 infil 1 0.0844 0.7714 blast 1 0.0208 0.8852 NOTE: No (additional) effects met the 0.3 significance level for entry into the model.
| |
| |
Summary of Stepwise Selection Effect Number Score Wald Step Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq 1 li 1 1 7.9311 0.0049 2 temp 1 2 1.2591 0.2618 3 cell 1 3 1.4700 0.2254
| |
Prior to the first step, the intercept-only model is fitted and individual score statistics for the potential variables are evaluated (Output 42.1.1). In Step 1 (Output 42.1.2), variable li is selected into the model since it is the most significant variable among those to be chosen ( p =0 . 0049 < 0 . 3). The intermediate model that contains an intercept and li is then fitted. li remains significant ( p =0 . 0146 < 0 . 35) and is not removed. In Step 2 (Output 42.1.3), variable temp is added to the model. The model then contains an intercept and variables li and temp . Both li and temp remain significant at 0.035 level; therefore, neither li nor temp is removed from the model. In Step 4 (Output 42.1.4), variable cell is added to the model. The model then contains an intercept and variables li , temp , and cell . None of these variables are removed from the model since all are significant at the 0.35 level. Finally, none of the remaining variables outside the model meet the entry criterion, and the stepwise selection is terminated . A summary of the stepwise selection is displayed in Output 42.1.5.
| |
Partition for the Hosmer and Lemeshow Test remiss = 1 remiss = 0 Group Total Observed Expected Observed Expected 1 3 0 0.00 3 3.00 2 3 0 0.01 3 2.99 3 3 0 0.19 3 2.81 4 3 0 0.56 3 2.44 5 4 1 1.09 3 2.91 6 3 2 1.35 1 1.65 7 3 2 1.84 1 1.16 8 3 3 2.15 0 0.85 9 2 1 1.80 1 0.20 Hosmer and Lemeshow Goodness-of-Fit Test Chi-Square DF Pr > ChiSq 6.2983 7 0.5054
| |
Results of the Hosmer and Lemeshow test are shown in Output 42.1.6. There is no evidence of a lack of fit in the selected model ( p =0 . 5054).
| |
Stepwise Regression on Cancer Remission Data Parameter Estimates and Covariance Matrix Obs _LINK_ _TYPE_ _STATUS_ _NAME_ Intercept cell 1 LOGIT PARMS 0 Converged remiss 67.63 9.652 2 LOGIT COV 0 Converged Intercept 3236.19 157.097 3 LOGIT COV 0 Converged cell 157.10 60.079 4 LOGIT COV 0 Converged smear . . 5 LOGIT COV 0 Converged infil . . 6 LOGIT COV 0 Converged li 64.57 6.945 7 LOGIT COV 0 Converged blast . . 8 LOGIT COV 0 Converged temp 3483.23 223.669 Obs smear infil li blast temp _LNLIKE_ 1 . . 3.8671 . 82.07 10.9767 2 . . 64.5726 . 3483.23 10.9767 3 . . 6.9454 . 223.67 10.9767 4 . . . . . 10.9767 5 . . . . . 10.9767 6 . . 3.1623 . 75.35 10.9767 7 . . . . . 10.9767 8 . . 75.3513 . 3808.42 10.9767
| |
The data set betas created by the OUTEST= and COVOUT options is displayed in Output 42.1.7. The data set contains parameter estimates and the covariance matrix for the final selected model. Note that all explanatory variables listed in the MODEL statement are included in this data set; however, variables that are not included in the final model have all missing values.
| |
Stepwise Regression on Cancer Remission Data Predicted Probabilities and 95% Confidence Limits _ r _ _ L e s i b F I E m c m n l t R N I I X X V p O i e e f a e O T P P P P E h l u b s l a i l s m M O _ _ _ _ L a c c s s l r l i t p _ _ 0 1 0 1 _ t l l 1 1 0.80 0.83 0.66 1.9 1.100 0.996 1 1 0.27735 0.72265 0.43873 0.56127 1 0.72265 0.16892 0.97093 2 1 0.90 0.36 0.32 1.4 0.740 0.992 1 1 0.42126 0.57874 0.47461 0.52539 1 0.57874 0.26788 0.83762 3 0 0.80 0.88 0.70 0.8 0.176 0.982 0 0 0.89540 0.10460 0.87060 0.12940 1 0.10460 0.00781 0.63419 4 0 1.00 0.87 0.87 0.7 1.053 0.986 0 0 0.71742 0.28258 0.67259 0.32741 1 0.28258 0.07498 0.65683 5 1 0.90 0.75 0.68 1.3 0.519 0.980 1 1 0.28582 0.71418 0.36901 0.63099 1 0.71418 0.25218 0.94876 6 0 1.00 0.65 0.65 0.6 0.519 0.982 0 0 0.72911 0.27089 0.67269 0.32731 1 0.27089 0.05852 0.68951 7 1 0.95 0.97 0.92 1.0 1.230 0.992 1 0 0.67844 0.32156 0.72923 0.27077 1 0.32156 0.13255 0.59516 8 0 0.95 0.87 0.83 1.9 1.354 1.020 0 1 0.39277 0.60723 0.09906 0.90094 1 0.60723 0.10572 0.95287 9 0 1.00 0.45 0.45 0.8 0.322 0.999 0 0 0.83368 0.16632 0.80864 0.19136 1 0.16632 0.03018 0.56123 10 0 0.95 0.36 0.34 0.5 0.000 1.038 0 0 0.99843 0.00157 0.99840 0.00160 1 0.00157 0.00000 0.68962 11 0 0.85 0.39 0.33 0.7 0.279 0.988 0 0 0.92715 0.07285 0.91723 0.08277 1 0.07285 0.00614 0.49982 12 0 0.70 0.76 0.53 1.2 0.146 0.982 0 0 0.82714 0.17286 0.63838 0.36162 1 0.17286 0.00637 0.87206 13 0 0.80 0.46 0.37 0.4 0.380 1.006 0 0 0.99654 0.00346 0.99644 0.00356 1 0.00346 0.00001 0.46530 14 0 0.20 0.39 0.08 0.8 0.114 0.990 0 0 0.99982 0.00018 0.99981 0.00019 1 0.00018 0.00000 0.96482 15 0 1.00 0.90 0.90 1.1 1.037 0.990 0 1 0.42878 0.57122 0.35354 0.64646 1 0.57122 0.25303 0.83973 16 1 1.00 0.84 0.84 1.9 2.064 1.020 1 1 0.28530 0.71470 0.47213 0.52787 1 0.71470 0.15362 0.97189 17 0 0.65 0.42 0.27 0.5 0.114 1.014 0 0 0.99938 0.00062 0.99937 0.00063 1 0.00062 0.00000 0.62665 18 0 1.00 0.75 0.75 1.0 1.322 1.004 0 0 0.77711 0.22289 0.73612 0.26388 1 0.22289 0.04483 0.63670 19 0 0.50 0.44 0.22 0.6 0.114 0.990 0 0 0.99846 0.00154 0.99842 0.00158 1 0.00154 0.00000 0.79644 20 1 1.00 0.63 0.63 1.1 1.072 0.986 1 1 0.35089 0.64911 0.42053 0.57947 1 0.64911 0.26305 0.90555 21 0 1.00 0.33 0.33 0.4 0.176 1.010 0 0 0.98307 0.01693 0.98170 0.01830 1 0.01693 0.00029 0.50475 22 0 0.90 0.93 0.84 0.6 1.591 1.020 0 0 0.99378 0.00622 0.99348 0.00652 1 0.00622 0.00003 0.56062 23 1 1.00 0.58 0.58 1.0 0.531 1.002 1 0 0.74739 0.25261 0.84423 0.15577 1 0.25261 0.06137 0.63597 24 0 0.95 0.32 0.30 1.6 0.886 0.988 0 1 0.12989 0.87011 0.03637 0.96363 1 0.87011 0.40910 0.98481 25 1 1.00 0.60 0.60 1.7 0.964 0.990 1 1 0.06868 0.93132 0.08017 0.91983 1 0.93132 0.44114 0.99573 26 1 1.00 0.69 0.69 0.9 0.398 0.986 1 0 0.53949 0.46051 0.62312 0.37688 1 0.46051 0.16612 0.78529 27 0 1.00 0.73 0.73 0.7 0.398 0.986 0 0 0.71742 0.28258 0.67259 0.32741 1 0.28258 0.07498 0.65683
| |
The data set pred created by the OUTPUT statement is displayed in Output 42.1.8.It contains all the variables in the input data set, the variable phat for the (cumulative) predicted probability, the variables lcl and ucl for the lower and upper confidence limits for the probability, and four other variables (viz., IP_1 , IP_0 , XP_1 , and XP_0 ) for the PREDPROBS= option. The data set also contains the variable _LEVEL_ , indicating the response value to which phat , lcl , and ucl refer. For instance, for the first row of the OUTPUT data set, the values of _LEVEL_ and phat , lcl , and ucl are 1, 0.72265, 0.16892 and 0.97093, respectively; this means that the estimated probability that remiss ‰ 1 is 0.723 for the given explanatory variable values, and the corresponding 95% confidence interval is (0.16892, 0.97093). The variables IP_1 and IP_0 contain the predicted probabilities that remiss =1 and remiss =0, respectively. Note that values of phat and IP_1 are identical since they both contain the probabilities that remiss =1. The variables XP_1 and XP_0 contain the cross validated predicted probabilities that remiss =1 and remiss =0, respectively.
Next , a different variable selection method is used to select prognostic factors for cancer remission, and an efficient algorithm is employed to eliminate insignificant variables from a model. The following SAS statements invoke PROC LOGISTIC to perform the backward elimination analysis.
title Backward Elimination on Cancer Remission Data; proc logistic data=Remission; model remiss(event=1)=temp cell li smear blast / selection=backward fast slstay=0.2 ctable; run;
The backward elimination analysis (SELECTION=BACKWARD) starts with a model that contains all explanatory variables given in the MODEL statement. By specifying the FAST option, PROC LOGISTIC eliminates insignificant variables without refitting the model repeatedly. This analysis uses a significance level of 0.2 (SLSTAY=0.2) to retain variables in the model, which is different from the previous stepwise analysis where SLSTAY=.35. The CTABLE option is specified to produce classifications of input observations based on the final selected model.
| |
Backward Elimination on Cancer Remission Data The LOGISTIC Procedure Model Information Data Set WORK.REMISSION Response Variable remiss Complete Remission Number of Response Levels 2 Model binary logit Optimization Technique Fishers scoring Number of Observations Read 27 Number of Observations Used 27 Response Profile Ordered Total Value remiss Frequency 1 0 18 2 1 9 Probability modeled is remiss=1. Backward Elimination Procedure Step 0. The following effects were entered: Intercept temp cell li smear blast Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 36.372 33.857 SC 37.668 41.632 -2 Log L 34.372 21.857 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 12.5146 5 0.0284 Score 9.3295 5 0.0966 Wald 4.7284 5 0.4499
| |
| |
Step 1. Fast Backward Elimination: Analysis of Effects Removed by Fast Backward Elimination Pr > Effect Residual Residual Removed Chi-Square DF Pr > ChiSq Chi-Square DF ChiSq blast 0.0008 1 0.9768 0.0008 1 0.9768 smear 0.0951 1 0.7578 0.0959 2 0.9532 cell 1.5134 1 0.2186 1.6094 3 0.6573 temp 0.6535 1 0.4189 2.2628 4 0.6875 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 36.372 30.073 SC 37.668 32.665 -2 Log L 34.372 26.073 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 8.2988 1 0.0040 Score 7.9311 1 0.0049 Wald 5.9594 1 0.0146 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 2.8530 4 0.5827 Summary of Backward Elimination Effect Number Wald Step Removed DF In Chi-Square Pr > ChiSq 1 blast 1 4 0.0008 0.9768 1 smear 1 3 0.0951 0.7578 1 cell 1 2 1.5134 0.2186 1 temp 1 1 0.6535 0.4189 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -3.7771 1.3786 7.5064 0.0061 li 1 2.8973 1.1868 5.9594 0.0146 Association of Predicted Probabilities and Observed Responses Percent Concordant 84.0 Somers D 0.710 Percent Discordant 13.0 Gamma 0.732 Percent Tied 3.1 Tau-a 0.328 Pairs 162 c 0.855
| |
Results of the fast elimination analysis are shown in Output 42.1.9 and Output 42.1.10. Initially, a full model containing all six risk factors is fit to the data (Output 42.1.9). In the next step (Output 42.1.10), PROC LOGISTIC removes blast , smear , cell , and temp from the model all at once. This leaves li and the intercept as the only variables in the final model. Note that in this analysis, only parameter estimates for the final model are displayed because the DETAILS option has not been specified.
Note that you can also use the FAST option when SELECTION=STEPWISE. However, the FAST option operates only on backward elimination steps. In this example, the stepwise process only adds variables, so the FAST option would not be useful.
| |
Classification Table Correct Incorrect Percentages Prob Non- Non- Sensi- Speci- False False Level Event Event Event Event Correct tivity ficity POS NEG 0.060 9 0 18 0 33.3 100.0 0.0 66.7 . 0.080 9 2 16 0 40.7 100.0 11.1 64.0 0.0 0.100 9 4 14 0 48.1 100.0 22.2 60.9 0.0 0.120 9 4 14 0 48.1 100.0 22.2 60.9 0.0 0.140 9 7 11 0 59.3 100.0 38.9 55.0 0.0 0.160 9 10 8 0 70.4 100.0 55.6 47.1 0.0 0.180 9 10 8 0 70.4 100.0 55.6 47.1 0.0 0.200 8 13 5 1 77.8 88.9 72.2 38.5 7.1 0.220 8 13 5 1 77.8 88.9 72.2 38.5 7.1 0.240 8 13 5 1 77.8 88.9 72.2 38.5 7.1 0.260 6 13 5 3 70.4 66.7 72.2 45.5 18.8 0.280 6 13 5 3 70.4 66.7 72.2 45.5 18.8 0.300 6 13 5 3 70.4 66.7 72.2 45.5 18.8 0.320 6 14 4 3 74.1 66.7 77.8 40.0 17.6 0.340 5 14 4 4 70.4 55.6 77.8 44.4 22.2 0.360 5 14 4 4 70.4 55.6 77.8 44.4 22.2 0.380 5 15 3 4 74.1 55.6 83.3 37.5 21.1 0.400 5 15 3 4 74.1 55.6 83.3 37.5 21.1 0.420 5 15 3 4 74.1 55.6 83.3 37.5 21.1 0.440 5 15 3 4 74.1 55.6 83.3 37.5 21.1 0.460 4 16 2 5 74.1 44.4 88.9 33.3 23.8 0.480 4 16 2 5 74.1 44.4 88.9 33.3 23.8 0.500 4 16 2 5 74.1 44.4 88.9 33.3 23.8 0.520 4 16 2 5 74.1 44.4 88.9 33.3 23.8 0.540 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.560 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.580 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.600 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.620 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.640 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.660 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.680 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.700 3 16 2 6 70.4 33.3 88.9 40.0 27.3 0.720 2 16 2 7 66.7 22.2 88.9 50.0 30.4 0.740 2 16 2 7 66.7 22.2 88.9 50.0 30.4 0.760 2 16 2 7 66.7 22.2 88.9 50.0 30.4 0.780 2 16 2 7 66.7 22.2 88.9 50.0 30.4 0.800 2 17 1 7 70.4 22.2 94.4 33.3 29.2 0.820 2 17 1 7 70.4 22.2 94.4 33.3 29.2 0.840 0 17 1 9 63.0 0.0 94.4 100.0 34.6 0.860 0 17 1 9 63.0 0.0 94.4 100.0 34.6 0.880 0 17 1 9 63.0 0.0 94.4 100.0 34.6 0.900 0 17 1 9 63.0 0.0 94.4 100.0 34.6 0.920 0 17 1 9 63.0 0.0 94.4 100.0 34.6 0.940 0 17 1 9 63.0 0.0 94.4 100.0 34.6 0.960 0 18 0 9 66.7 0.0 100.0 . 33.3
| |
Results of the CTABLE option are shown in Output 42.1.11. Each row of the Classification Table corresponds to a cutpoint applied to the predicted probabilities, which is given in the Prob Level column. The 2 — 2 frequency tables of observed and predicted responses are given by the next four columns . For example, with a cutpoint of 0.5, 4 events and 16 nonevents were classified correctly. On the other hand, 2 nonevents were incorrectly classified as events and 5 events were incorrectly classified as nonevents. For this cutpoint, the correct classification rate is 20/27 (=74.1%), which is given in the sixth column. Accuracy of the classification is summarized by the sensitivity, specificity, and false positive and negative rates, which are displayed in the last four columns. You can control the number of cutpoints used, and their values,byusingthePPROB= option.
Example 42.2. Logistic Modeling with Categorical Predictors
Consider a study of the analgesic effects of treatments on elderly patients with neuralgia. Two test treatments and a placebo are compared. The response variable is whether the patient reported pain or not. Researchers recorded age and gender of the patients and the duration of complaint before the treatment began . The data, consisting of 60 patients, are contained in the data set Neuralgia .
Data Neuralgia; input Treatment $ Sex $ Age Duration Pain $ @@; datalines; P F 68 1 No B M 74 16 No P F 67 30 No P M 66 26 Yes B F 67 28 No B F 77 16 No A F 71 12 No B F 72 50 No B F 76 9 Yes A M 71 17 Yes A F 63 27 No A F 69 18 Yes B F 66 12 No A M 62 42 No P F 64 1 Yes A F 64 17 No P M 74 4 No A F 72 25 No P M 70 1 Yes B M 66 19 No B M 59 29 No A F 64 30 No A M 70 28 No A M 69 1 No B F 78 1 No P M 83 1 Yes B F 69 42 No B M 75 30 Yes P M 77 29 Yes P F 79 20 Yes A M 70 12 No A F 69 12 No B F 65 14 No B M 70 1 No B M 67 23 No A M 76 25 Yes P M 78 12 Yes B M 77 1 Yes B F 69 24 No P M 66 4 Yes P F 65 29 No P M 60 26 Yes A M 78 15 Yes B M 75 21 Yes A F 67 11 No P F 72 27 No P F 70 13 Yes A M 75 6 Yes B F 65 7 No P F 68 27 Yes P M 68 11 Yes P M 67 17 Yes B M 70 22 No A M 65 15 No P F 67 1 Yes A M 67 10 No P F 72 11 Yes A F 74 1 No B M 80 21 Yes A F 69 3 No ;
The data set Neuralgia contains five variables: Treatment , Sex , Age , Duration ,and Pain . The last variable, Pain , is the response variable. A specification of Pain =Yes indicates there was pain, and Pain =No indicates no pain. The variable Treatment is a categorical variable with three levels: A and B represent the two test treatments, and P represents the placebo treatment. The gender of the patients is given by the categorical variable Sex . The variable Age is the age of the patients, in years , when treatment began. The duration of complaint, in months, before the treatment began is given by the variable Duration . The following statements use the LOGISTIC procedure to fit a two-way logit with interaction model for the effect of Treatment and Sex , with Age and Duration as covariates. The categorical variables Treatment and Sex are declared in the CLASS statement.
proc logistic data=Neuralgia; class Treatment Sex; model Pain= Treatment Sex Treatment*Sex Age Duration / expb; run;
In this analysis, PROC LOGISTIC models the probability of no pain ( Pain =No). By default, effect coding is used to represent the CLASS variables. Two design variables are created for Treatment and one for Sex , as shown in Output 42.2.1.
| |
The LOGISTIC Procedure Class Level Information Design Class Value Variables Treatment A 1 0 B 0 1 P -1 -1 Sex F 1 M -1
| |
PROC LOGISTIC displays a table of the Type 3 analysis of effects based on the Wald test (Output 42.2.2). Note that the Treatment*Sex interaction and the duration of complaint are not statistically significant ( p =0.9318 and p =0.8752, respectively). This indicates that there is no evidence that the treatments affect pain differently in men and women, and no evidence that the pain outcome is related to the duration of pain.
| |
Type 3 Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq Treatment 2 11.9886 0.0025 Sex 1 5.3104 0.0212 Treatment*Sex 2 0.1412 0.9318 Age 1 7.2744 0.0070 Duration 1 0.0247 0.8752
| |
Parameter estimates are displayed in Output 42.2.3. The Exp(Est) column contains the exponentiated parameter estimates requested with the EXPB option. These values may, but do not necessarily , represent odds ratios for the corresponding variables. For continuous explanatory variables, the Exp(Est) value corresponds to the odds ratio for a unit increase of the corresponding variable. For CLASS variables using the effect coding, the Exp(Est) values have no direct interpretation as a comparison of levels. However, when the reference coding is used, the Exp(Est) values represent the odds ratio between the corresponding level and the last level. Following the parameter estimates table, PROC LOGISTIC displays the odds ratio estimates for those variables that are not involved in any interaction terms. If the variable is a CLASS variable, the odds ratio estimate comparing each level with the last level is computed regardless of the coding scheme. In this analysis, since the model contains the Treatment * Sex interaction term , the odds ratios for Treatment and Sex were not computed. The odds ratio estimates for Age and Duration are precisely the values given in the Exp(Est) column in the parameter estimates table.
| |
Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Exp(Est) Intercept 1 19.2236 7.1315 7.2661 0.0070 2.232E8 Treatment A 1 0.8483 0.5502 2.3773 0.1231 2.336 Treatment B 1 1.4949 0.6622 5.0956 0.0240 4.459 Sex F 1 0.9173 0.3981 5.3104 0.0212 2.503 Treatment*Sex A F 1 -0.2010 0.5568 0.1304 0.7180 0.818 Treatment*Sex B F 1 0.0487 0.5563 0.0077 0.9302 1.050 Age 1 -0.2688 0.0996 7.2744 0.0070 0.764 Duration 1 0.00523 0.0333 0.0247 0.8752 1.005 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits Age 0.764 0.629 0.929 Duration 1.005 0.942 1.073
| |
The following PROC LOGISTIC statements illustrate the use of forward selection on the data set Neuralgia to identify the effects that differentiate the two Pain responses. The option SELECTION=FORWARD is specified to carry out the forward selection. The term TreatmentSex@2 illustrates another way to specify main effects and two-way interaction as is available in other procedures such as PROC GLM. (Note that, in this case, the @2 is unnecessary because no interactions besides the two-way interaction are possible).
proc logistic data=Neuralgia; class Treatment Sex; model Pain=TreatmentSex@2 Age Duration /selection=forward expb; run;
Results of the forward selection process are summarized in Output 42.2.4. The variable Treatment is selected first, followed by Age and then Sex . The results are consistent with the previous analysis (Output 42.2.2) in which the Treatment * Sex interaction and Duration are not statistically significant.
| |
The LOGISTIC Procedure Summary of Forward Selection Effect Number Score Step Entered DF In Chi-Square Pr > ChiSq 1 Treatment 2 1 13.7143 0.0011 2 Age 1 2 10.6038 0.0011 3 Sex 1 3 5.9959 0.0143
| |
Output 42.2.5 shows the Type 3 analysis of effects, the parameter estimates, and the odds ratio estimates for the selected model. All three variables, Treatment , Age , and Sex , are statistically significant at the 0.05 level ( p =0.0011, p =0.0011, and p =0.0143, respectively). Since the selected model does not contain the Treatment * Sex interaction, odds ratios for Treatment and Sex are computed. The estimated odds ratio is 24.022 for treatment A versus placebo, 41.528 for Treatment B versus placebo, and 6.194 for female patients versus male patients. Note that these odds ratio estimates are not the same as the corresponding values in the Exp(Est) column in the parameter estimates table because effect coding was used. From Output 42.2.5, it is evident that both Treatment A and Treatment B are better than the placebo in reducing pain; females tend to have better improvement than males; and younger patients are faring better than older patients.
| |
Type 3 Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq Treatment 2 12.6928 0.0018 Sex 1 5.3013 0.0213 Age 1 7.6314 0.0057 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Exp(Est) Intercept 1 19.0804 6.7882 7.9007 0.0049 1.9343E8 Treatment A 1 0.8772 0.5274 2.7662 0.0963 2.404 Treatment B 1 1.4246 0.6036 5.5711 0.0183 4.156 Sex F 1 0.9118 0.3960 5.3013 0.0213 2.489 Age 1 -0.2650 0.0959 7.6314 0.0057 0.767 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits Treatment A vs P 24.022 3.295 175.121 Treatment B vs P 41.528 4.500 383.262 Sex F vs M 6.194 1.312 29.248 Age 0.767 0.636 0.926
| |
Finally, PROC LOGISTIC is invoked to refit the previously selected model using reference coding for the CLASS variables. Two CONTRAST statements are specified. The one labeled Pairwise specifies three rows in the contrast matrix, L, for all the pairwise comparisons between the three levels of Treatment . The contrast labeled Female vs Male compares female to male patients. The option ESTIMATE=EXP is specified in both CONTRAST statements to exponentiate the estimates of L ² ² . With the given specification of contrast coefficients, the first row of the Pairwise CONTRAST statement corresponds to the odds ratio of A versus P, the second row corresponds to B versus P, and the third row corresponds to A versus B. There is only one row in the Female vs Male CONTRAST statement, and it corresponds to the odds ratio comparing female to male patients.
proc logistic data=Neuralgia; class Treatment Sex /param=ref; model Pain= Treatment Sex age; contrast Pairwise Treatment 1 0, Treatment 0 1, Treatment 1 -1 / estimate=exp; contrast Female vs Male Sex 1 / estimate=exp; run;
| |
The LOGISTIC Procedure Class Level Information Design Class Value Variables Treatment A 1 0 B 0 1 P 0 0 Sex F 1 M 0
| |
The reference coding is shown in Output 42.2.6. The Type 3 analysis of effects, the parameter estimates for the reference coding, and the odds ratio estimates are displayed in Output 42.2.7. Although the parameter estimates are different (because of the different parameterizations), the Type 3 Analysis of Effects table and the Odds Ratio table remain the same as in Output 42.2.5. With effect coding, the treatment A parameter estimate (0.8772) estimates the effect of treatment A compared to the average effect of treatments A, B, and placebo. The treatment A estimate (3.1790) under the reference coding estimates the difference in effect of treatment A and the placebo treatment.
| |
Type 3 Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq Treatment 2 12.6928 0.0018 Sex 1 5.3013 0.0213 Age 1 7.6314 0.0057 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 15.8669 6.4056 6.1357 0.0132 Treatment A 1 3.1790 1.0135 9.8375 0.0017 Treatment B 1 3.7264 1.1339 10.8006 0.0010 Sex F 1 1.8235 0.7920 5.3013 0.0213 Age 1 -0.2650 0.0959 7.6314 0.0057 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits Treatment A vs P 24.022 3.295 175.121 Treatment B vs P 41.528 4.500 383.262 Sex F vs M 6.194 1.312 29.248 Age 0.767 0.636 0.926
| |
Output 42.2.8 contains two tables: the Contrast Test Results table and the Contrast Rows Estimation and Testing Results table. The former contains the overall Wald test for each CONTRAST statement. Although three rows are specified in the Pairwise CONTRAST statement, there are only two degrees of freedom, and the Wald test result is identical to the Type 3 analysis of Treatment in Output 42.2.7. The latter table contains estimates and tests of individual contrast rows. The estimates for the first two rows of the Pairwise CONTRAST statement are the same as those given in the Odds Ratio Estimates table (in Output 42.2.7). Both treatments A and B are highly effective over placebo in reducing pain. The third row estimates the odds ratio comparing A to B. The 95% confidence interval for this odds ratio is (0.0932, 3.5889), indicating that the pain reduction effects of these two test treatments are not that different. Again, the Female vs Male contrast shows that female patients fared better in obtaining relief from pain than male patients.
| |
Contrast Test Results Wald Contrast DF Chi-Square Pr > ChiSq Pairwise 2 12.6928 0.0018 Female vs Male 1 5.3013 0.0213 Contrast Rows Estimation and Testing Results Standard Contrast Type Row Estimate Error Alpha Confidence Limits Pairwise EXP 1 24.0218 24.3473 0.05 3.2951 175.1 Pairwise EXP 2 41.5284 47.0877 0.05 4.4998 383.3 Pairwise EXP 3 0.5784 0.5387 0.05 0.0932 3.5889 Female vs Male EXP 1 6.1937 4.9053 0.05 1.3116 29.2476 Contrast Rows Estimation and Testing Results Wald Contrast Type Row Chi-Square Pr > ChiSq Pairwise EXP 1 9.8375 0.0017 Pairwise EXP 2 10.8006 0.0010 Pairwise EXP 3 0.3455 0.5567 Female vs Male EXP 1 5.3013 0.0213
| |
Example 42.3. Ordinal Logistic Regression
Consider a study of the effects on taste of various cheese additives. Researchers tested four cheese additives and obtained 52 response ratings for each additive. Each response was measured on a scale of nine categories ranging from strong dislike (1) to excellent taste (9). The data, given in McCullagh and Nelder (1989, p. 175) in the form of a two-way frequency table of additive by rating, are saved in the data set Cheese .
data Cheese; do Additive = 1 to 4; do y = 1 to 9; input freq @@; output; end; end; label y=Taste Rating; datalines; 0 0 1 7 8 8 19 8 1 6 9 12 11 7 6 1 0 0 1 1 6 8 23 7 5 1 0 0 0 0 1 3 7 14 16 11 ;
The data set Cheese contains the variables y , Additive , and freq . The variable y contains the response rating. The variable Additive specifies the cheese additive (1, 2, 3, or 4). The variable freq gives the frequency with which each additive received each rating.
The response variable y is ordinally scaled. A cumulative logit model is used to investigate the effects of the cheese additives on taste. The following SAS statements invoke PROC LOGISTIC to fit this model with y as the response variable and three indicator variables as explanatory variables, with the fourth additive as the reference level. With this parameterization, each Additive parameter compares an additive to the fourth additive. The COVB option produces the estimated covariance matrix.
Proc logistic data=Cheese; freq freq; class Additive (param=ref ref=4); model y=Additive / covb; title1 Multiple Response Cheese Tasting Experiment; run;
Results of the analysis are shown in Output 42.3.1, and the estimated covariance matrix is displayed in Output 42.3.2.
| |
Multiple Response Cheese Tasting Experiment The LOGISTIC Procedure Model Information Data Set WORK.CHEESE Response Variable y Taste Rating Number of Response Levels 9 Frequency Variable freq Model cumulative logit Optimization Technique Fishers scoring Number of Observations Read 36 Number of Observations Used 28 Sum of Frequencies Read 208 Sum of Frequencies Used 208 Response Profile Ordered Total Value y Frequency 1 1 7 2 2 10 3 3 19 4 4 27 5 5 41 6 6 28 7 7 39 8 8 25 9 9 12 Probabilities modeled are cumulated over the lower Ordered Values. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Score Test for the Proportional Odds Assumption Chi-Square DF Pr > ChiSq 17.2866 21 0.6936 Multiple Response Cheese Tasting Experiment Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 875.802 733.348 SC 902.502 770.061 -2 Log L 859.802 711.348 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 148.4539 3 <.0001 Score 111.2670 3 <.0001 Wald 115.1504 3 <.0001 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 1 -7.0801 0.5624 158.4851 <.0001 Intercept 2 1 -6.0249 0.4755 160.5500 <.0001 Intercept 3 1 -4.9254 0.4272 132.9484 <.0001 Intercept 4 1 -3.8568 0.3902 97.7087 <.0001 Intercept 5 1 -2.5205 0.3431 53.9704 <.0001 Intercept 6 1 -1.5685 0.3086 25.8374 <.0001 Intercept 7 1 -0.0669 0.2658 0.0633 0.8013 Intercept 8 1 1.4930 0.3310 20.3439 <.0001 Additive 1 1 1.6128 0.3778 18.2265 <.0001 Additive 2 1 4.9645 0.4741 109.6427 <.0001 Additive 3 1 3.3227 0.4251 61.0931 <.0001 Association of Predicted Probabilities and Observed Responses Percent Concordant 67.6 Somers D 0.578 Percent Discordant 9.8 Gamma 0.746 Percent Tied 22.6 Tau-a 0.500 Pairs 18635 c 0.789
| |
| |
Multiple Response Cheese Tasting Experiment Estimated Covariance Matrix Intercept_ Intercept_ Intercept_ Intercept_ Intercept_ Parameter 1 2 3 4 5 Intercept_1 0.316291 0.219581 0.176278 0.147694 0.114024 Intercept_2 0.219581 0.226095 0.177806 0.147933 0.11403 Intercept_3 0.176278 0.177806 0.182473 0.148844 0.114092 Intercept_4 0.147694 0.147933 0.148844 0.152235 0.114512 Intercept_5 0.114024 0.11403 0.114092 0.114512 0.117713 Intercept_6 0.091085 0.091081 0.091074 0.091109 0.091821 Intercept_7 0.057814 0.057813 0.057807 0.05778 0.057721 Intercept_8 0.041304 0.041304 0.0413 0.041277 0.041162 Additive1 -0.09419 -0.09421 -0.09427 -0.09428 -0.09246 Additive2 -0.18686 -0.18161 -0.1687 -0.14717 -0.11415 Additive3 -0.13565 -0.13569 -0.1352 -0.13118 -0.11207 Estimated Covariance Matrix Intercept_ Intercept_ Intercept_ Parameter 6 7 8 Additive1 Additive2 Additive3 Intercept_1 0.091085 0.057814 0.041304 -0.09419 -0.18686 -0.13565 Intercept_2 0.091081 0.057813 0.041304 -0.09421 -0.18161 -0.13569 Intercept_3 0.091074 0.057807 0.0413 -0.09427 -0.1687 -0.1352 Intercept_4 0.091109 0.05778 0.041277 -0.09428 -0.14717 -0.13118 Intercept_5 0.091821 0.057721 0.041162 -0.09246 -0.11415 -0.11207 Intercept_6 0.09522 0.058312 0.041324 -0.08521 -0.09113 -0.09122 Intercept_7 0.058312 0.07064 0.04878 -0.06041 -0.05781 -0.05802 Intercept_8 0.041324 0.04878 0.109562 -0.04436 -0.0413 -0.04143 Additive1 -0.08521 -0.06041 -0.04436 0.142715 0.094072 0.092128 Additive2 -0.09113 -0.05781 -0.0413 0.094072 0.22479 0.132877 Additive3 -0.09122 -0.05802 -0.04143 0.092128 0.132877 0.180709
| |
Since the strong dislike ( y =1) end of the rating scale is associated with lower Ordered Values in the Response Profile table, the probability of disliking the additives is modeled.
The score chi-square for testing the proportional odds assumption is 17.287, which is not significant with respect to a chi-square distribution with 21 degrees of freedom ( p =0 . 694). This indicates that the proportional odds model adequately fits the data. The positive value (1.6128) for the parameter estimate for Additive1 indicates a tendency towards the lower-numbered categories of the first cheese additive relative to the fourth. In other words, the fourth additive is better in taste than the first additive. Each of the second and the third additives is less favorable than the fourth additive. The relative magnitudes of these slope estimates imply the preference ordering: fourth, first, third, second.
Example 42.4. Nominal Response Data: Generalized Logits Model
Over the course of one school year, third graders from three different schools are exposed to three different styles of mathematics instruction: a self-paced computer-learning style, a team approach, and a traditional class approach. The students are asked which style they prefer and their responses, classified by the type of program they are in (a regular school day versus a regular day supplemented with an afternoon school program) are displayed in Table 42.4. The data set is from Stokes, Davis, and Koch (2000), and is also analyzed in the Generalized Logits Model section on page 824 of Chapter 22, The CATMOD Procedure.
| Learning Style Preference | ||||
|---|---|---|---|---|
| School | Program | Self | Team | Class |
| 1 | Regular | 10 | 17 | 26 |
| 1 | Afternoon | 5 | 12 | 50 |
| 2 | Regular | 21 | 17 | 26 |
| 2 | Afternoon | 16 | 12 | 36 |
| 3 | Regular | 15 | 15 | 16 |
| 3 | Afternoon | 12 | 12 | 20 |
The levels of the response variable (self, team, and class) have no essential ordering, so a logistic regression is performed on the generalized logits. The model to be fit is
where hij is the probability that a student in school h and program i prefers teaching style j , j ‰ r , and style r is the baseline style (in this case, class). There are separate sets of intercept parameters ± j and regression parameters ² j for each logit, and the matrix x hi is the set of explanatory variables for the hi th population. Thus, two logits are modeled for each school and program combination: the logit comparing self to class and the logit comparing team to class.
The following statements create the data set school and request the analysis. The LINK=GLOGIT option forms the generalized logits. The response variable option ORDER=DATA means that the response variable levels are ordered as they exist in the data set: self, team, and class; thus, the logits are formed by comparing self to class and by comparing team to class. The ODS statement suppresses the display of the maximum likelihood estimates. The results of this analysis are shown in Output 42.4.1 through Output 42.4.4.
| |
The LOGISTIC Procedure Model Information Data Set WORK.SCHOOL Response Variable Style Number of Response Levels 3 Frequency Variable Count Model generalized logit Optimization Technique Fishers scoring Number of Observations Read 18 Number of Observations Used 18 Sum of Frequencies Read 338 Sum of Frequencies Used 338 Response Profile Ordered Total Value Style Frequency 1 self 79 2 team 85 3 class 174 Logits modeled use Style=class as the reference category. Class Level Information Design Class Value Variables School 1 1 0 2 0 1 3 -1 -1 Program afternoon -1 regular 1
| |
data school; length Program $ 9; input School Program $ Style $ Count @@; datalines; 1 regular self 10 1 regular team 17 1 regular class 26 1 afternoon self 5 1 afternoon team 12 1 afternoon class 50 2 regular self 21 2 regular team 17 2 regular class 26 2 afternoon self 16 2 afternoon team 12 2 afternoon class 36 3 regular self 15 3 regular team 15 3 regular class 16 3 afternoon self 12 3 afternoon team 12 3 afternoon class 20 ; proc logistic data=school; freq Count; class School Program(ref=first); model Style(order=data)=School Program School*Program / link=glogit; run;
| |
Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 699.404 689.156 SC 707.050 735.033 -2 Log L 695.404 665.156
| |
| |
Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 30.2480 10 0.0008 Score 28.3738 10 0.0016 Wald 25.6828 10 0.0042 Type 3 Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq School 4 14.5522 0.0057 Program 2 10.4815 0.0053 School*Program 4 1.7439 0.7827
| |
| |
Analysis of Maximum Likelihood Estimates Standard Wald Parameter Style DF Estimate Error Chi-Square Pr > ChiSq Intercept self 1 -0.8097 0.1488 29.5989 <.0001 Intercept team 1 -0.6585 0.1366 23.2449 <.0001 School 1 self 1 -0.8194 0.2281 12.9066 0.0003 School 1 team 1 -0.2675 0.1881 2.0233 0.1549 School 2 self 1 0.2974 0.1919 2.4007 0.1213 School 2 team 1 -0.1033 0.1898 0.2961 0.5863 Program regular self 1 0.3985 0.1488 7.1684 0.0074 Program regular team 1 0.3537 0.1366 6.7071 0.0096 School*Program 1 regular self 1 0.2751 0.2281 1.4547 0.2278 School*Program 1 regular team 1 0.1474 0.1881 0.6143 0.4332 School*Program 2 regular self 1 -0.0998 0.1919 0.2702 0.6032 School*Program 2 regular team 1 -0.0168 0.1898 0.0079 0.9293
| |
The Type 3 Analysis of Effects table in Output 42.4.3 shows that the interaction effect is clearly nonsignificant, so a main effects model is fit with the following statements.
proc logistic data=school; freq Count; class School Program(ref=first); model Style(order=data)=School Program / link=glogit; run;
| |
The LOGISTIC Procedure Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 699.404 682.934 SC 707.050 713.518 -2 Log L 695.404 666.934 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 28.4704 6 <.0001 Score 27.1190 6 0.0001 Wald 25.5881 6 0.0003 Type 3 Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq School 4 14.8424 0.0050 Program 2 10.9160 0.0043
| |
All of the global fit tests in Output 42.4.5 suggest the model is significant, and the Type 3 tests show that the school and program effects are also significant.
| |
Analysis of Maximum Likelihood Estimates Standard Wald Parameter Style DF Estimate Error Chi-Square Pr > ChiSq Intercept self 1 -0.7978 0.1465 29.6502 <.0001 Intercept team 1 -0.6589 0.1367 23.2300 <.0001 School 1 self 1 -0.7992 0.2198 13.2241 0.0003 School 1 team 1 -0.2786 0.1867 2.2269 0.1356 School 2 self 1 0.2836 0.1899 2.2316 0.1352 School 2 team 1 -0.0985 0.1892 0.2708 0.6028 Program regular self 1 0.3737 0.1410 7.0272 0.0080 Program regular team 1 0.3713 0.1353 7.5332 0.0061 Odds Ratio Estimates Point 95% Wald Effect Style Estimate Confidence Limits School 1 vs 3 self 0.269 0.127 0.570 School 1 vs 3 team 0.519 0.267 1.010 School 2 vs 3 self 0.793 0.413 1.522 School 2 vs 3 team 0.622 0.317 1.219 Program regular vs afternoon self 2.112 1.215 3.670 Program regular vs afternoon team 2.101 1.237 3.571
| |
The parameter estimates, tests for individual parameters, and odds ratios are displayed in Output 42.4.6. The Program variable has nearly the same effect on both logits, while School =1 has the largest effect of the schools.
Example 42.5. Stratified Sampling
Consider the hypothetical example in Fleiss (1981, pp. 6 “7) in which a test is applied to a sample of 1,000 people known to have a disease and to another sample of 1,000 people known not to have the same disease. In the diseased sample, 950 test positive; in the nondiseased sample, only 10 test positive. If the true disease rate in the population is 1 in 100, specifying PEVENT=0.01 results in the correct false positive and negative rates for the stratified sampling scheme. Omitting the PEVENT= option is equivalent to using the overall sample disease rate (1000/2000 = 0.5) as the value of the PEVENT= option, which would ignore the stratified sampling.
The SAS code is as follows :
data Screen; do Disease=Present,Absent; do Test=1,0; input Count @@; output; end; end; datalines; 950 50 10 990 ; proc logistic data=Screen; freq Count; model Disease(event=Present)=Test / pevent=.5 .01 ctable pprob=.5; run;
The response variable option EVENT= indicates that Disease = Present is the event. The CTABLE option is specified to produce a classification table. Specifying PPROB=0.5 indicates a cutoff probability of 0.5. A list of two probabilities, 0.5 and 0.01, is specified for the PEVENT= option; 0.5 corresponds to the overall sample disease rate, and 0.01 corresponds to a true disease rate of 1 in 100.
The classification table is shown in Output 42.5.1.
| |
The LOGISTIC Procedure Classification Table Correct Incorrect Percentages Prob Prob Non- Non- Sensi- Speci- False False Event Level Event Event Event Event Correct tivity ficity POS NEG 0.500 0.500 950 990 10 50 97.0 95.0 99.0 1.0 4.8 0.010 0.500 950 990 10 50 99.0 95.0 99.0 51.0 0.1
| |
In the classification table, the column Prob Level represents the cutoff values (the settings of the PPROB= option) for predicting whether an observation is an event. The Correct columns list the numbers of subjects that are correctly predicted as events and nonevents, respectively, and the Incorrect columns list the number of nonevents incorrectly predicted as events and the number of events incorrectly predicted as nonevents, respectively. For PEVENT=0.5, the false positive rate is 1% and the false negative rate is 4.8%. These results ignore the fact that the samples were stratified and incorrectly assume that the overall sample proportion of disease (which is 0.5) estimates the true disease rate. For a true disease rate of 0.01, the false positive rate and the false negative rate are 51% and 0.1%, respectively, as shown on the second line of the classification table.
Example 42.6. Logistic Regression Diagnostics
In a controlled experiment to study the effect of the rate and volume of air inspired on a transient reflex vaso-constriction in the skin of the digits, 39 tests under various combinations of rate and volume of air inspired were obtained (Finney 1947). The end point of each test is whether or not vaso-constriction occurred. Pregibon (1981) uses this set of data to illustrate the diagnostic measures he proposes for detecting influential observations and to quantify their effects on various aspects of the maximum likelihood fit.
The vaso-constriction data are saved in the data set vaso :
data vaso; length Response ; input Volume Rate Response @@; LogVolume=log(Volume); LogRate=log(Rate); datalines; 3.70 0.825 constrict 3.50 1.09 constrict 1.25 2.50 constrict 0.75 1.50 constrict 0.80 3.20 constrict 0.70 3.50 constrict 0.60 0.75 no_constrict 1.10 1.70 no_constrict 0.90 0.75 no_constrict 0.90 0.45 no_constrict 0.80 0.57 no_constrict 0.55 2.75 no_constrict 0.60 3.00 no_constrict 1.40 2.33 constrict 0.75 3.75 constrict 2.30 1.64 constrict 3.20 1.60 constrict 0.85 1.415 constrict 1.70 1.06 no_constrict 1.80 1.80 constrict 0.40 2.00 no_constrict 0.95 1.36 no_constrict 1.35 1.35 no_constrict 1.50 1.36 no_constrict 1.60 1.78 constrict 0.60 1.50 no_constrict 1.80 1.50 constrict 0.95 1.90 no_constrict 1.90 0.95 constrict 1.60 0.40 no_constrict 2.70 0.75 constrict 2.35 0.03 no_constrict 1.10 1.83 no_constrict 1.10 2.20 constrict 1.20 2.00 constrict 0.80 3.33 constrict 0.95 1.90 no_constrict 0.75 1.90 no_constrict 1.30 1.625 constrict ;
In the data set vaso , the variable Response represents the outcome of a test. The variable LogVolume represents the log of the volume of air intake, and the variable LogRate represents the log of the rate of air intake.
The following SAS statements invoke PROC LOGISTIC to fit a logistic regression model to the vaso-constriction data, where Response is the response variable, and LogRate and LogVolume are the explanatory variables. The INFLUENCE option and the IPLOTS option are specified to display the regression diagnostics and the index plots.
ods html; ods graphics on; title Occurrence of Vaso-Constriction; proc logistic data=vaso; model Response=LogRate LogVolume/influence iplots; run; ods graphics off; ods html close;
Results of the model fit are shown in Output 42.6.1. Both LogRate and LogVolume are statistically significant to the occurrence of vaso-constriction ( p =0 . 0131 and p =0 . 0055, respectively). Their positive parameter estimates indicate that a higher inspiration rate or a larger volume of air intake is likely to increase the probability of vaso-constriction.
| |
Occurrence of Vaso-Constriction The LOGISTIC Procedure Model Information Data Set WORK.VASO Response Variable Response Number of Response Levels 2 Model binary logit Optimization Technique Fishers scoring Number of Observations Read 39 Number of Observations Used 39 Response Profile Ordered Total Value Response Frequency 1 constrict 20 2 no_constrict 19 Probability modeled is Response=constrict. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Occurrence of Vaso-Constriction Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 56.040 35.227 SC 57.703 40.218 -2 Log L 54.040 29.227 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 24.8125 2 <.0001 Score 16.6324 2 0.0002 Wald 7.8876 2 0.0194 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.8754 1.3208 4.7395 0.0295 LogRate 1 4.5617 1.8380 6.1597 0.0131 LogVolume 1 5.1793 1.8648 7.7136 0.0055 Association of Predicted Probabilities and Observed Responses Percent Concordant 93.7 Somers D 0.874 Percent Discordant 6.3 Gamma 0.874 Percent Tied 0.0 Tau-a 0.448 Pairs 380 c 0.937
| |
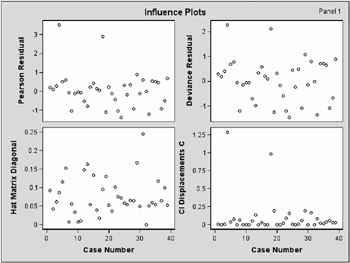
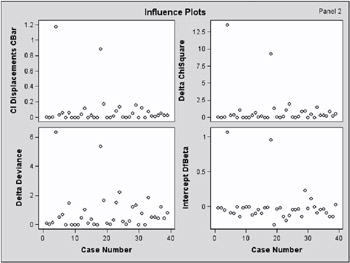
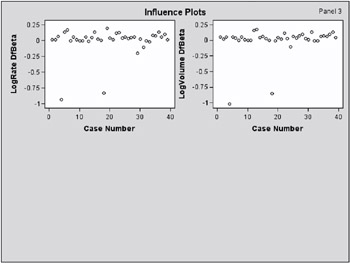
The INFLUENCE option displays the values of the explanatory variables ( LogRate and LogVolume ) for each observation, a column for each diagnostic produced, and the case number which represents the sequence number of the observation (Output 42.6.2). Also produced (but not shown here) is a lineprinter plot where the vertical axis represents the case number and the horizontal axis represents the value of the diagnostic statistic.
The index plots produced by the IPLOTS option are essentially the same lineprinter plots as those produced by the INFLUENCE option with a 90-degree rotation and perhaps on a more refined scale. This version of the plots are not displayed here. The vertical axis of an index plot represents the value of the diagnostic and the horizontal axis represents the sequence (case number) of the observation. The index plots are useful for identification of extreme values.
Since the experimental ODS GRAPHICS statement is also specified, the lineprinter plots from the INFLUENCE and IPLOTS options are suppressed and graphical displays are produced as shown in Output 42.6.3 through Output 42.6.5. For general information about ODS graphics, see Chapter 15, Statistical Graphics Using ODS. For specific information about the graphics available in the LOGISTIC procedure, see the ODS Graphics section on page 2388.
| |
The LOGISTIC Procedure Regression Diagnostics Covariates Hat Case Log Pearson Deviance Matrix Intercept LogRate Number LogRate Volume Residual Residual Diagonal DfBeta DfBeta 1 -0.1924 1.3083 0.2205 0.3082 0.0927 -0.0165 0.0193 2 0.0862 1.2528 0.1349 0.1899 0.0429 -0.0134 0.0151 3 0.9163 0.2231 0.2923 0.4049 0.0612 -0.0492 0.0660 4 0.4055 -0.2877 3.5181 2.2775 0.0867 1.0734 -0.9302 5 1.1632 -0.2231 0.5287 0.7021 0.1158 -0.0832 0.1411 6 1.2528 -0.3567 0.6090 0.7943 0.1524 -0.0922 0.1710 7 -0.2877 -0.5108 -0.0328 -0.0464 0.00761 -0.00280 0.00274 8 0.5306 0.0953 -1.0196 -1.1939 0.0559 -0.1444 0.0613 9 -0.2877 -0.1054 -0.0938 -0.1323 0.0342 -0.0178 0.0173 10 -0.7985 -0.1054 -0.0293 -0.0414 0.00721 -0.00245 0.00246 11 -0.5621 -0.2231 -0.0370 -0.0523 0.00969 -0.00361 0.00358 12 1.0116 -0.5978 -0.5073 -0.6768 0.1481 -0.1173 0.0647 13 1.0986 -0.5108 -0.7751 -0.9700 0.1628 -0.0931 -0.00946 14 0.8459 0.3365 0.2559 0.3562 0.0551 -0.0414 0.0538 15 1.3218 -0.2877 0.4352 0.5890 0.1336 -0.0940 0.1408 16 0.4947 0.8329 0.1576 0.2215 0.0402 -0.0198 0.0234 17 0.4700 1.1632 0.0709 0.1001 0.0172 -0.00630 0.00701 18 0.3471 -0.1625 2.9062 2.1192 0.0954 0.9595 -0.8279 19 0.0583 0.5306 -1.0718 -1.2368 0.1315 -0.2591 0.2024 20 0.5878 0.5878 0.2405 0.3353 0.0525 -0.0331 0.0421 21 0.6931 -0.9163 -0.1076 -0.1517 0.0373 -0.0180 0.0158 22 0.3075 -0.0513 -0.4193 -0.5691 0.1015 -0.1449 0.1237 23 0.3001 0.3001 -1.0242 -1.1978 0.0761 -0.1961 0.1275 24 0.3075 0.4055 -1.3684 -1.4527 0.0717 -0.1281 0.0410 25 0.5766 0.4700 0.3347 0.4608 0.0587 -0.0403 0.0570 26 0.4055 -0.5108 -0.1595 -0.2241 0.0548 -0.0366 0.0329 27 0.4055 0.5878 0.3645 0.4995 0.0661 -0.0327 0.0496 28 0.6419 -0.0513 -0.8989 -1.0883 0.0647 -0.1423 0.0617 29 -0.0513 0.6419 0.8981 1.0876 0.1682 0.2367 -0.1950 30 -0.9163 0.4700 -0.0992 -0.1400 0.0507 -0.0224 0.0227 31 -0.2877 0.9933 0.6198 0.8064 0.2459 0.1165 -0.0996 32 -3.5066 0.8544 -0.00073 -0.00103 0.000022 -3.22E-6 3.405E-6 33 0.6043 0.0953 -1.2062 -1.3402 0.0510 -0.0882 -0.0137 34 0.7885 0.0953 0.5447 0.7209 0.0601 -0.0425 0.0877 35 0.6931 0.1823 0.5404 0.7159 0.0552 -0.0340 0.0755 36 1.2030 -0.2231 0.4828 0.6473 0.1177 -0.0867 0.1381 37 0.6419 -0.0513 -0.8989 -1.0883 0.0647 -0.1423 0.0617 38 0.6419 -0.2877 -0.4874 -0.6529 0.1000 -0.1395 0.1032 39 0.4855 0.2624 0.7053 0.8987 0.0531 0.0326 0.0190 The LOGISTIC Procedure Regression Diagnostics Confidence Confidence Log Interval Interval Case Volume Displacement Displacement Delta Delta Number DfBeta C CBar Deviance Chi-Square 1 0.0556 0.00548 0.00497 0.1000 0.0536 2 0.0261 0.000853 0.000816 0.0369 0.0190 3 0.0589 0.00593 0.00557 0.1695 0.0910 4 -1.0180 1.2873 1.1756 6.3626 13.5523 5 0.0583 0.0414 0.0366 0.5296 0.3161 6 0.0381 0.0787 0.0667 0.6976 0.4376 7 0.00265 8.321E-6 8.258E-6 0.00216 0.00109 8 0.0570 0.0652 0.0616 1.4870 1.1011 9 0.0153 0.000322 0.000311 0.0178 0.00911 10 0.00211 6.256E-6 6.211E-6 0.00172 0.000862 11 0.00319 0.000014 0.000013 0.00274 0.00138 12 0.1651 0.0525 0.0447 0.5028 0.3021 13 0.1775 0.1395 0.1168 1.0577 0.7175 14 0.0527 0.00404 0.00382 0.1307 0.0693 15 0.0643 0.0337 0.0292 0.3761 0.2186 16 0.0307 0.00108 0.00104 0.0501 0.0259 17 0.00914 0.000089 0.000088 0.0101 0.00511 18 -0.8477 0.9845 0.8906 5.3817 9.3363 19 -0.00488 0.2003 0.1740 1.7037 1.3227 20 0.0518 0.00338 0.00320 0.1156 0.0610 21 0.0208 0.000465 0.000448 0.0235 0.0120 22 0.1179 0.0221 0.0199 0.3437 0.1956 23 0.0357 0.0935 0.0864 1.5212 1.1355 24 -0.1004 0.1558 0.1447 2.2550 2.0171 25 0.0708 0.00741 0.00698 0.2193 0.1190 26 0.0373 0.00156 0.00147 0.0517 0.0269 27 0.0788 0.0101 0.00941 0.2589 0.1423 28 0.1025 0.0597 0.0559 1.2404 0.8639 29 0.0286 0.1961 0.1631 1.3460 0.9697 30 0.0159 0.000554 0.000526 0.0201 0.0104 31 0.1322 0.1661 0.1253 0.7755 0.5095 32 2.48E-6 1.18E-11 1.18E-11 1.065E-6 5.324E-7 33 -0.00216 0.0824 0.0782 1.8744 1.5331 34 0.0671 0.0202 0.0190 0.5387 0.3157 35 0.0711 0.0180 0.0170 0.5295 0.3091 36 0.0631 0.0352 0.0311 0.4501 0.2641 37 0.1025 0.0597 0.0559 1.2404 0.8639 38 0.1397 0.0293 0.0264 0.4526 0.2639 39 0.0489 0.0295 0.0279 0.8355 0.5254
| |
| |
| |
| |
| |
The index plots of the Pearson residuals and the deviance residuals (Output 42.6.3) indicate that case 4 and case 18 are poorly accounted for by the model. The index plot of the diagonal elements of the hat matrix (Output 42.6.3) suggests that case 31 is an extreme point in the design space. The index plots of DFBETAS (Output 42.6.4 and Output 42.6.5) indicate that case 4 and case 18 are causing instability in all three parameter estimates. The other four index plots in Output 42.6.3 and Output 42.6.4 also point to these two cases as having a large impact on the coefficients and goodness of fit.
Example 42.7. ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits
This example plots an ROC curve, estimates a customized odds ratio, produces the traditional goodness-of-fit analysis, displays the generalized R 2 measures for the fitted model, calculates the normal confidence intervals for the regression parameters, and produces an experimental display of the probability function and prediction curves for the fitted model. The data consist of three variables: n (number of subjects in a sample), disease (number of diseased subjects in the sample), and age (age for the sample). A linear logistic regression model is used to study the effect of age on the probability of contracting the disease.
The SAS statements are as follows:
data Data1; input disease n age; datalines; 0 14 25 0 20 35 0 19 45 7 18 55 6 12 65 17 17 75 ; ods html; ods graphics on; proc logistic data=Data1; model disease/n=age / scale=none clparm=wald clodds=pl rsquare outroc=roc1; units age=10; run; ods graphics off; ods html close;
The option SCALE=NONE is specified to produce the deviance and Pearson goodness-of-fit analysis without adjusting for overdispersion. The RSQUARE option is specified to produce generalized R 2 measures of the fitted model. The CLPARM=WALD option is specified to produce the Wald confidence intervals for the regression parameters. The UNITS statement is specified to produce customized odds ratio estimates for a change of 10 years in the age variable, and the CLODDS=PL option is specified to produce profile likelihood confidence limits for the odds ratio. The OUTROC= option outputs the data for the ROC curve to the SAS data set, roc1 .
Results are shown in Output 42.7.1 and Output 42.7.2.
| |
Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 124.173 52.468 SC 126.778 57.678 -2 Log L 122.173 48.468 R-Square 0.5215 Max-rescaled R-Square 0.7394 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 73.7048 1 <.0001 Score 55.3274 1 <.0001 Wald 23.3475 1 <.0001 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.5016 2.5555 23.9317 <.0001 age 1 0.2066 0.0428 23.3475 <.0001 Association of Predicted Probabilities and Observed Responses Percent Concordant 92.6 Somers D 0.906 Percent Discordant 2.0 Gamma 0.958 Percent Tied 5.4 Tau-a 0.384 Pairs 2100 c 0.953 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -12.5016 -17.5104 -7.4929 age 0.2066 0.1228 0.2904 Profile Likelihood Confidence Interval for Adjusted Odds Ratios Effect Unit Estimate 95% Confidence Limits age 10.0000 7.892 3.881 21.406
| |
| |
The LOGISTIC Procedure Deviance and Pearson Goodness-of-Fit Statistics Criterion Value DF Value/DF Pr > ChiSq Deviance 7.7756 4 1.9439 0.1002 Pearson 6.6020 4 1.6505 0.1585 Number of events/trials observations: 6
| |
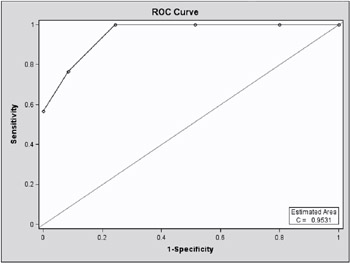
Since the experimental ODS GRAPHICS statement is specified, a graphical display of the ROC curve is produced as shown in Output 42.7.3. For general information about ODS graphics, see Chapter 15, Statistical Graphics Using ODS. For specific information about the graphics available in the LOGISTIC procedure, see the ODS Graphics section on page 2388.
| |
| |
Note that the area under the ROC curve is given by the statistic c in the Association of Predicted Probabilities and Observed Responses table. In this example, the area under the ROC curve is 0.953.
The ROC curve may also be displayed with the GPLOT procedure by using the following code.
symbol1 i=join v=none c=black; proc gplot data=roc1; title ROC Curve; plot _sensit_*_1mspec_=1 / vaxis=0 to 1 by .1 cframe=white; run;
Because there is only one continuous covariate, if the experimental ODS GRAPHICS statement and the experimental GRAPHICS option ESTPROB are specified, then a graphical display of the estimated probability curve with bounding 95% prediction limits is displayed as shown in Output 42.7.4.
| |

| |
ods html; ods graphics on; proc logistic data=Data1; model disease/n=age / scale=none clparm=wald clodds=pl rsquare outroc=roc1; units age=10; graphics estprob; run; ods graphics off; ods html close;
Example 42.8. Goodness-of-Fit Tests and Subpopulations
A study is done to investigate the effects of two binary factors, A and B , on a binary response, Y . Subjects are randomly selected from subpopulations defined by the four possible combinations of levels of A and B . The number of subjects responding with each level of Y is recorded and entered into data set A .
data a; do A=0,1; do B=0,1; do Y=1,2; input F @@; output; end; end; end; datalines; 23 63 31 70 67 100 70 104 ;
A full model is fit to examine the main effects of A and B as well as the interaction effect of A and B .
proc logistic data=a; freq F; model Y=A B A*B; run;
| |
The LOGISTIC Procedure Model Information Data Set WORK.A Response Variable Y Number of Response Levels 2 Frequency Variable F Model binary logit Optimization Technique Fishers scoring Number of Observations Read 8 Number of Observations Used 8 Sum of Frequencies Read 528 Sum of Frequencies Used 528 Response Profile Ordered Total Value Y Frequency 1 1 191 2 2 337 Probability modeled is Y=1. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 693.061 691.914 SC 697.330 708.990 -2 Log L 691.061 683.914 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 7.1478 3 0.0673 Score 6.9921 3 0.0721 Wald 6.9118 3 0.0748 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.0074 0.2436 17.1015 <.0001 A 1 0.6069 0.2903 4.3714 0.0365 B 1 0.1929 0.3254 0.3515 0.5533 A*B 1 -0.1883 0.3933 0.2293 0.6321 Association of Predicted Probabilities and Observed Responses Percent Concordant 42.2 Somers D 0.118 Percent Discordant 30.4 Gamma 0.162 Percent Tied 27.3 Tau-a 0.054 Pairs 64367 c 0.559
| |
Pearson and Deviance goodness-of-fit tests cannot be obtained for this model since a full model containing four parameters is fit, leaving no residual degrees of freedom. For a binary response model, the goodness-of-fittestshave m ˆ’ q degrees of freedom, where m is the number of subpopulations and q is the number of model parameters. In the preceding model, m = q =4, resulting in zero degrees of freedom for the tests.
Results of the model fit are shown in Output 42.8.1. Notice that neither the A * B interaction nor the B main effect is significant. If a reduced model containing only the A effect is fit, two degrees of freedom become available for testing goodness of fit. Specifying the SCALE=NONE option requests the Pearson and deviance statistics. With single-trial syntax, the AGGREGATE= option is needed to define the subpopulations in the study. Specifying AGGREGATE=(A B) creates subpopulations of the four combinations of levels of A and B . Although the B effect is being dropped from the model, it is still needed to define the original subpopulations in the study. If AGGREGATE=(A) were specified, only two subpopulations would be created from the levels of A , resulting in m = q = 2 and zero degrees of freedom for the tests.
proc logistic data=a; freq F; model Y=A / scale=none aggregate=(A B); run;
| |
The LOGISTIC Procedure Model Information Data Set WORK.A Response Variable Y Number of Response Levels 2 Frequency Variable F Model binary logit Optimization Technique Fishers scoring Number of Observations Read 8 Number of Observations Used 8 Sum of Frequencies Read 528 Sum of Frequencies Used 528 Response Profile Ordered Total Value Y Frequency 1 1 191 2 2 337 Probability modeled is Y=1. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Deviance and Pearson Goodness-of-Fit Statistics Criterion Value DF Value/DF Pr > ChiSq Deviance 0.3541 2 0.1770 0.8377 Pearson 0.3531 2 0.1765 0.8382 Number of unique profiles: 4 Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 693.061 688.268 SC 697.330 696.806 -2 Log L 691.061 684.268 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 6.7937 1 0.0091 Score 6.6779 1 0.0098 Wald 6.6210 1 0.0101 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.9013 0.1614 31.2001 <.0001 A 1 0.5032 0.1955 6.6210 0.0101 Association of Predicted Probabilities and Observed Responses Percent Concordant 28.3 Somers D 0.112 Percent Discordant 17.1 Gamma 0.246 Percent Tied 54.6 Tau-a 0.052 Pairs 64367 c 0.556
| |
The goodness-of-fittests(Output 42.8.2) show that dropping the B main effect and the A * B interaction simultaneously does not result in significant lack of fitofthe model. The tests large p -values indicate insufficient evidence for rejecting the null hypothesis that the model fits.
Example 42.9. Overdispersion
In a seed germination test, seeds of two cultivars were planted in pots of two soil conditions. The following SAS statements create the data set seeds , which contains the observed proportion of seeds that germinated for various combinations of cultivar and soil condition. Variable n represents the number of seeds planted in a pot, and variable r represents the number germinated. The indicator variables cult and soil represent the cultivar and soil condition, respectively.
data seeds; input pot n r cult soil; datalines; 1 16 8 0 0 2 51 26 0 0 3 45 23 0 0 4 39 10 0 0 5 36 9 0 0 6 81 23 1 0 7 30 10 1 0 8 39 17 1 0 9 28 8 1 0 10 62 23 1 0 11 51 32 0 1 12 72 55 0 1 13 41 22 0 1 14 12 3 0 1 15 13 10 0 1 16 79 46 1 1 17 30 15 1 1 18 51 32 1 1 19 74 53 1 1 20 56 12 1 1 ;
PROC LOGISTIC is used to fit a logit model to the data, with cult , soil , and cult — soil interaction as explanatory variables. The option SCALE=NONE is specified to display goodness-of-fit statistics.
proc logistic data=seeds; model r/n=cult soil cult*soil/scale=none; title 'Full Model With SCALE=NONE'; run;
| |
Full Model With SCALE=NONE The LOGISTIC Procedure Deviance and Pearson Goodness-of-Fit Statistics Criterion Value DF Value/DF Pr > ChiSq Deviance 68.3465 16 4.2717 <.0001 Pearson 66.7617 16 4.1726 <.0001 Number of events/trials observations: 20 Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 1256.852 1213.003 SC 1261.661 1232.240 2 Log L 1254.852 1205.003 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 49.8488 3 <.0001 Score 49.1682 3 <.0001 Wald 47.7623 3 <.0001 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 0.3788 0.1489 6.4730 0.0110 cult 1 0.2956 0.2020 2.1412 0.1434 soil 1 0.9781 0.2128 21.1234 <.0001 cult*soil 1 0.1239 0.2790 0.1973 0.6569
| |
Results of fitting the full factorial model are shown in Output 42.9.1. Both Pearson 2 and deviance are highly significant ( p < 0.0001), suggesting that the model does not fit well. If the link function and the model specification are correct and if there are no outliers, then the lack of fit may be due to overdispersion. Without adjusting for the overdispersion, the standard errors are likely to be underestimated, causing the Wald tests to be too sensitive. In PROC LOGISTIC, there are three SCALE= options to accommodate overdispersion. With unequal sample sizes for the observations, SCALE=WILLIAMS is preferred. The Williams model estimates a scale parameter by equating the value of Pearson 2 for the full model to its approximate expected value. The full model considered here is the model with cultivar, soil condition, and their interaction. Using a full model reduces the risk of contaminating with lack of fit due to incorrect model specification.
proc logistic data=seeds; model r/n=cult soil cult*soil / scale=williams; title 'Full Model With SCALE=WILLIAMS'; run;
Results using Williams method are shown in Output 42.9.2. The estimate of ![]() is 0.075941 and is given in the formula for the Weight Variable at the beginning of the displayed output. Since neither cult nor cult — soil is statistically significant ( p = 0.5290 and p = 0.9274, respectively), a reduced model that contains only the soil condition factor is fitted, with the observations weighted by 1 / (1+0 . 075941( N ˆ’ 1)). This can be done conveniently in PROC LOGISTIC by including the scale estimate in the SCALE=WILLIAMS option as follows:
is 0.075941 and is given in the formula for the Weight Variable at the beginning of the displayed output. Since neither cult nor cult — soil is statistically significant ( p = 0.5290 and p = 0.9274, respectively), a reduced model that contains only the soil condition factor is fitted, with the observations weighted by 1 / (1+0 . 075941( N ˆ’ 1)). This can be done conveniently in PROC LOGISTIC by including the scale estimate in the SCALE=WILLIAMS option as follows:
| |
Full Model With SCALE=WILLIAMS The LOGISTIC Procedure Model Information Data Set WORK.SEEDS Response Variable (Events) r Response Variable (Trials) n Weight Variable 1 / (1 + 0.075941 * (n 1)) Model binary logit Optimization Technique Fishers scoring Number of Observations Read 20 Number of Observations Used 20 Sum of Frequencies Read 906 Sum of Frequencies Used 906 Sum of Weights Read 198.3216 Sum of Weights Used 198.3216 Response Profile Ordered Binary Total Total Value Outcome Frequency Weight 1 Event 437 92.95346 2 Nonevent 469 105.36819 Model Convergence Status Convergence criterion (GCONV=1E 8) satisfied. Deviance and Pearson Goodness-of-Fit Statistics Criterion Value DF Value/DF Pr > ChiSq Deviance 16.4402 16 1.0275 0.4227 Pearson 16.0000 16 1.0000 0.4530 Number of events/trials observations: 20 NOTE: Since the Williams method was used to accommodate overdispersion, the Pearson chi-squared statistic and the deviance can no longer be used to assess the goodness of fit of the model. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 276.155 273.586 SC 280.964 292.822 2 Log L 274.155 265.586 Full Model With SCALE=WILLIAMS Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 8.5687 3 0.0356 Score 8.4856 3 0.0370 Wald 8.3069 3 0.0401 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 0.3926 0.2932 1.7932 0.1805 cult 1 0.2618 0.4160 0.3963 0.5290 soil 1 0.8309 0.4223 3.8704 0.0491 cult*soil 1 0.0532 0.5835 0.0083 0.9274 Association of Predicted Probabilities and Observed Responses Percent Concordant 50.6 Somers' D 0.258 Percent Discordant 24.8 Gamma 0.343 Percent Tied 24.6 Tau-a 0.129 Pairs 204953 c 0.629
| |
proc logistic data=seeds; model r/n=soil / scale=williams(0.075941); title 'Reduced Model With SCALE=WILLIAMS(0.075941)'; run;
Results of the reduced model fit are shown in Output 42.9.3. Soil condition remains a significant factor ( p = 0 . 0064) for the seed germination.
| |
Reduced Model With SCALE=WILLIAMS(0.075941) The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 0.5249 0.2076 6.3949 0.0114 soil 1 0.7910 0.2902 7.4284 0.0064 | |
Example 42.10. Conditional Logistic Regression for Matched Pairs Data
In matched pairs, or case-control , studies, conditional logistic regression is used to investigate the relationship between an outcome of being an event (case) or a nonevent (control) and a set of prognostic factors.
The data in this example are a subset of the data from the Los Angeles Study of the Endometrial Cancer Data in Breslow and Day (1980). There are 63 matched pairs, each consisting of a case of endometrial cancer ( Outcome =1) and a control ( Outcome =0). The case and corresponding control have the same ID . Two prognostic factors are included: Gall (an indicator variable for gall bladder disease) and Hyper (an indicator variable for hypertension). The goal of the case-control analysis is to determine the relative risk for gall bladder disease, controlling for the effect of hypertension.
data Data1; do ID=1 to 63; do Outcome = 1 to 0 by -1; input Gall Hyper @@; output; end; end; datalines; 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 1 1 0 1 0 1 0 0 1 0 1 0 0 0 0 1 1 0 0 1 1 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0 ;
There are several ways to approach this problem with PROC LOGISTIC.
-
Specify the STRATA statement to perform a conditional logistic regression.
-
Specify EXACT and STRATA statements to perform an exact conditional logistic regression on the original data set, if you believe the data set is too small or too sparse for the usual asymptotics to hold.
-
Transform each matched pair into a single observation then specify a PROC LOGISTIC statement on this transformed data without a STRATA statement; this also performs a conditional logistic regression and produces essentially the same results.
-
Specify an EXACT statement on the transformed data.
SAS statements and selected results for these four approaches are given in the remainder of this example.
Conditional Analysis Using the STRATA Statement
In the following SAS statements, PROC LOGISTIC is invoked with the ID variable declared in the STRATA statement to obtain the conditional logistic model estimates. Two models are fitted. The first model contains Gall as the only predictor variable, and the second model contains both Gall and Hyper as predictor variables. Because the option CLODDS=Wald is specified, PROC LOGISTIC computes a 95% Wald confidence interval for the odds ratio for each predictor variable.
proc logistic data=Data1; strata ID; model outcome(event='1')=Gall / clodds=Wald; run; proc logistic data=Data1; strata ID; model outcome(event='1')=Gall Hyper /clodds=Wald; run;
Results from the two conditional logistic analyses are shown in Output 42.10.1 and Output 42.10.2. Note that there is only one response level listed in the Response Profile tables, and there is no intercept term in the Analysis of Maximum Likelihood Estimates tables.
| |
The LOGISTIC Procedure Conditional Analysis Model Information Data Set WORK.DATA1 Response Variable Outcome Number of Response Levels 2 Number of Strata 63 Model binary logit Optimization Technique Newton-Raphson ridge Number of Observations Read 126 Number of Observations Used 126 Response Profile Ordered Total Value Outcome Frequency 1 0 63 2 1 63 Probability modeled is Outcome=1. Strata Summary Outcome Response ------- Number of Pattern 0 1 Strata Frequency 1 1 1 63 126 Conditional Analysis Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Without With Criterion Covariates Covariates AIC 87.337 85.654 SC 87.337 88.490 2 Log L 87.337 83.654 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 3.6830 1 0.0550 Score 3.5556 1 0.0593 Wald 3.2970 1 0.0694 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Gall 1 0.9555 0.5262 3.2970 0.0694 Wald Confidence Interval for Adjusted Odds Ratios Effect Unit Estimate 95% Confidence Limits Gall 1.0000 2.600 0.927 7.293 | |
| |
The LOGISTIC Procedure Conditional Analysis Model Information Data Set WORK.DATA1 Response Variable Outcome Number of Response Levels 2 Number of Strata 63 Model binary logit Optimization Technique Newton-Raphson ridge Number of Observations Read 126 Number of Observations Used 126 Response Profile Ordered Total Value Outcome Frequency 1 0 63 2 1 63 Probability modeled is Outcome=1. Strata Summary Outcome Response ------- Number of Pattern 0 1 Strata Frequency 1 1 1 63 126 Conditional Analysis Convergence criterion (GCONV=1E 8) satisfied. Model Fit Statistics Without With Criterion Covariates Covariates AIC 87.337 86.788 SC 87.337 92.460 2 Log L 87.337 82.788 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 4.5487 2 0.1029 Score 4.3620 2 0.1129 Wald 4.0060 2 0.1349 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Gall 1 0.9704 0.5307 3.3432 0.0675 Hyper 1 0.3481 0.3770 0.8526 0.3558 Wald Confidence Interval for Adjusted Odds Ratios Effect Unit Estimate 95% Confidence Limits Gall 1.0000 2.639 0.933 7.468 Hyper 1.0000 1.416 0.677 2.965
| |
In the first model, where Gall is the only predictor variable (Output 42.10.1), the odds ratio estimate for Gall is 2.60, which is marginally significant ( p =0.0694) and which is an estimate of the relative risk for gall bladder disease. A 95% confidence interval for this relative risk is (0.927, 7.293).
In the second model, where both Gall and Hyper are present (Output 42.10.2), the odds ratio estimate for Gall is 2.639, which is an estimate of the relative risk for gall bladder disease adjusted for the effects of hypertension. A 95% confidence interval for this adjusted relative risk is (0.933, 7.468). Note that the adjusted values (accounting for hypertension) for gall bladder disease are not very different from the unadjusted values (ignoring hypertension). This is not surprising since the prognostic factor Hyper is highly statistically insignificant. The 95% Wald confidence interval for the odds ratio for Hyper is (0.677, 2.965), which contains unity with a p -value greater than 0 . 3.
Exact Analysis Using the STRATA Statement
When you believe there is not enough data or that the data are too sparse, you can perform a stratified exact conditional logistic regression. The following statements perform stratified exact conditional logistic regressions on the original data set by specifying both the STRATA and EXACT statements.
proc logistic data=Data1 exactonly; strata ID; model outcome(event='1')=Gall; exact Gall / estimate=both; run; proc logistic data=Data1 exactonly; strata ID; model outcome(event='1')=Gall Hyper; exact Gall Hyper / jointonly estimate=both; run;
Note that the score statistics in the Conditional Exact Tests tables in Output 42.10.3 and Output 42.10.4 are identical to the score statistics in the conditional analyses in Output 42.10.1 and Output 42.10.2, respectively. The exact odds ratio confidence intervals are much wider than their conditional analysis counterparts, but the parameter estimates are similar. The exact analyses confirm the marginal significance of Gall and the insignificance of Hyper as predictor variables.
| |
The LOGISTIC Procedure Exact Conditional Analysis Conditional Exact Tests --- p-Value -- Effect Test Statistic Exact Mid Gall Score 3.5556 0.0963 0.0799 Probability 0.0327 0.0963 0.0799 Exact Parameter Estimates 95% Confidence Parameter Estimate Limits p-Value Gall 0.9555 0.1394 2.2316 0.0963 Exact Odds Ratios 95% Confidence Parameter Estimate Limits p-Value Gall 2.600 0.870 9.315 0.0963 | |
| |
The LOGISTIC Procedure Exact Conditional Analysis Conditional Exact Tests --- p-Value --- Effect Test Statistic Exact Mid Joint Score 4.3620 0.1150 0.1134 Probability 0.00316 0.1150 0.1134 Exact Parameter Estimates 95% Confidence Parameter Estimate Limits p-Value Gall 0.9530 0.1407 2.2292 0.0969 Hyper 0.3425 0.4486 1.1657 0.4622 Exact Odds Ratios 95% Confidence Parameter Estimate Limits p-Value Gall 2.593 0.869 9.293 0.0969 Hyper 1.408 0.639 3.208 0.4622
| |
Conditional Analysis Using Transformed Data
When each matched set consists of one event and one nonevent, the conditional likelihood is given by
where x i 1 and x i are vectors representing the prognostic factors for the event and nonevent, respectively, of the i th matched set. This likelihood is identical to the likelihood of fitting a logistic regression model to a set of data with constant response, where the model contains no intercept term and has explanatory variables given by d i = x i 1 ˆ’ x i (Breslow 1982).
To apply this method, each matched pair is transformed into a single observation, where the variables Gall and Hyper contain the differences between the corresponding values for the case and the control (case ˆ’ control). The variable Outcome , which will be used as the response variable in the logistic regression model, is given a constant value of 0 (which is the Outcome value for the control, although any constant, numeric or character, will do).
data Data2; set Data1; drop id1 gall1 hyper1; retain id1 gall1 hyper1 0; if (ID = id1) then do; Gall=gall1-Gall; Hyper=hyper1-Hyper; output; end; else do; id1=ID; gall1=Gall; hyper1=Hyper; end; run;
Note that there are 63 observations in the data set, one for each matched pair. The variable Outcome has a constant value of 0.
In the following SAS statements, PROC LOGISTIC is invoked with the NOINT option to obtain the conditional logistic model estimates. Because the option CLODDS=PL is specified, PROC LOGISTIC computes a 95% profile likelihood confidence interval for the odds ratio for each predictor variable; note that profile likelihood confidence intervals are not currently available when a STRATA statement is specified.
proc logistic data=Data2; model outcome=Gall / noint clodds=PL; run; proc logistic data=Data2; model outcome=Gall Hyper / noint clodds=PL; run;
The results are not displayed here.
Exact Analysis Using Transformed Data
Sometimes the original data set in a matched-pairs study may be too large for the exact methods to handle. In such cases it may be possible to use the transformed data set. The following code performs exact conditional logistic regressions on the transformed data set. The results are not displayed here.
proc logistic data=Data2 exactonly; model outcome=Gall / noint; exact Gall / estimate=both; run; proc logistic data=Data2 exactonly; model outcome=Gall Hyper / noint; exact Gall Hyper / jointonly estimate=both; run;
Example 42.11. Complementary Log-Log Model for Infection Rates
Antibodies produced in response to an infectious disease like malaria remain in the body after the individual has recovered from the disease. A serological test detects the presence or absence of such antibodies. An individual with such antibodies is termed seropositive. In areas where the disease is endemic, the inhabitants are at fairly constant risk of infection. The probability of an individual never having been infected in Y years is exp( ˆ’ ¼ Y ), where ¼ is the mean number of infections per year (refer to the appendix of Draper, Voller, and Carpenter 1972). Rather than estimating the unknown ¼ , it is of interest to epidemiologists to estimate the probability of a person living in the area being infected in one year. This infection rate ³ is given by
The following statements create the data set sero , which contains the results of a serological survey of malarial infection. Individuals of nine age groups ( Group ) were tested. Variable A represents the midpoint of the age range for each age group. Variable N represents the number of individuals tested in each age group, and variable R represents the number of individuals that are seropositive.
data sero; input Group A N R; X=log(A); label X='Log of Midpoint of Age Range'; datalines; 1 1.5 123 8 2 4.0 132 6 3 7.5 182 18 4 12.5 140 14 5 17.5 138 20 6 25.0 161 39 7 35.0 133 19 8 47.0 92 25 9 60.0 74 44 ;
For the i th group with age midpoint A i , the probability of being seropositive is p i = 1 ˆ’ exp( ˆ’ ¼ A i ). It follows that
By fitting a binomial model with a complementary log-log link function and by using X=log(A) as an offset term, you can estimate ² = log( ¼ ) as an intercept parameter. The following SAS statements invoke PROC LOGISTIC to compute the maximum likelihood estimate of ² . The LINK=CLOGLOG option is specified to request the complementary log-log link function. Also specified is the CLPARM=PL option, which requests the profile likelihood confidence limits for ² .
proc logistic data=sero; model R/N= / offset=X link=cloglog clparm=pl scale=none; title 'Constant Risk of Infection'; run;
Results of fitting this constant risk model are shown in Output 42.11.1. The maximum likelihood estimate of ² = log( ¼ ) and its estimated standard error are ![]() = ˆ’ 4.6605 and
= ˆ’ 4.6605 and ![]() , respectively. The infection rate is estimated as
, respectively. The infection rate is estimated as
| |
Constant Risk of Infection The LOGISTIC Procedure Model Information Data Set WORK.SERO Response Variable (Events) R Response Variable (Trials) N Offset Variable X Log of Midpoint of Age Range Model binary cloglog Optimization Technique Fishers scoring Number of Observations Read 9 Number of Observations Used 9 Sum of Frequencies Read 1175 Sum of Frequencies Used 1175 Response Profile Ordered Binary Total Value Outcome Frequency 1 Event 193 2 Nonevent 982 Intercept-Only Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. 2 Log L = 967.1158 Deviance and Pearson Goodness-of-Fit Statistics Criterion Value DF Value/DF Pr > ChiSq Deviance 41.5032 8 5.1879 <.0001 Pearson 50.6883 8 6.3360 <.0001 Number of events/trials observations: 9 Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 4.6605 0.0725 4133.5626 <.0001 X 1 1.0000 0 . . Profile Likelihood Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept 4.6605 4.8057 4.5219
| |
The 95% confidence interval for ³ , obtained by back-transforming the 95% confidence interval for ² , is (0.0082, 0.0108); that is, there is a 95% chance that, in repeated sampling, the interval of 8 to 11 infections per thousand individuals contains the true infection rate.
The goodness of fit statistics for the constant risk model are statistically significant ( p < 0 . 0001), indicating that the assumption of constant risk of infection is not correct. You can fit a more extensive model by allowing a separate risk of infection for each age group. Suppose ¼ i is the mean number of infections per year for the i th age group. The probability of seropositive for the i th group with age midpoint A i is p i = 1 ˆ’ exp( ˆ’ µ i A i ), so that
In the following statements, a complementary log-log model is fit containing Group as an explanatory classification variable with the GLM coding (so that a dummy variable is created for each age group), no intercept term, and X=log(A) as an offset term. The ODS OUTPUT statement saves the estimates and their 95% profile likelihood confidence limits to ClparmPL data set. Note that log( ¼ i ) is the regression parameter associated with Group = i .
proc logistic data=sero; ods output ClparmPL=ClparmPL; class Group / param=glm; model R/N=Group / noint offset=X link=cloglog clparm=pl; title 'Infectious Rates and 95% Confidence Intervals'; run;
Results of fitting the model with a separate risk of infection are shown in Output 42.11.2. For the first age group ( Group =1), the point estimate of log( ¼ 1 ) is ˆ’ 3 . 1048, which transforms into an infection rate of 1 ˆ’ exp( ˆ’ exp( ˆ’ 3.1048)) = 0 . 0438. A 95% confidence interval for this infection rate is obtained by transforming the 95% confidence interval for log( ¼ 1 ). For the first age group, the lower and upper confidence limits are 1 ˆ’ exp( ˆ’ exp( ˆ’ 3 . 8880) = 0.0203 and 1 ˆ’ exp( ˆ’ exp( ˆ’ 2 . 4833)) = 0 . 0801, respectively; that is, there is a 95% chance that, in repeated sampling, the interval of 20 to 80 infections per thousand individuals contains the true infection rate.
| |
Infectious Rates and 95% Confidence Intervals The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi Square Pr > ChiSq Group 1 1 3.1048 0.3536 77.0877 <.0001 Group 2 1 4.4542 0.4083 119.0164 <.0001 Group 3 1 4.2769 0.2358 328.9593 <.0001 Group 4 1 4.7761 0.2674 319.0600 <.0001 Group 5 1 4.7165 0.2238 443.9920 <.0001 Group 6 1 4.5012 0.1606 785.1350 <.0001 Group 7 1 5.4252 0.2296 558.1114 <.0001 Group 8 1 4.9987 0.2008 619.4666 <.0001 Group 9 1 4.1965 0.1559 724.3157 <.0001 X 1 1.0000 0 . . Profile Likelihood Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Group 1 3.1048 3.8880 2.4833 Group 2 4.4542 5.3769 3.7478 Group 3 4.2769 4.7775 3.8477 Group 4 4.7761 5.3501 4.2940 Group 5 4.7165 5.1896 4.3075 Group 6 4.5012 4.8333 4.2019 Group 7 5.4252 5.9116 5.0063 Group 8 4.9987 5.4195 4.6289 Group 9 4.1965 4.5164 3.9037
| |
The following statements perform this transformation on the estimates and confidence limits saved in the ClparmPL data set; the resulting estimated infection rates in one year s time for each age group are displayed in Table 42.5. Note that the infection rate for the first age group is high compared to the other age groups.
data ClparmPL; set ClparmPL; Estimate=round(1000*(1-exp(-exp(Estimate)))); LowerCL =round(1000*(1-exp(-exp(LowerCL)))); UpperCL =round(1000*(1-exp(-exp(UpperCL)))); run;
| Number Infected per 1,000 People | |||
|---|---|---|---|
| Age Group | Estimate Point | 95% Confidence Limits | |
| Lower | Upper | ||
| 1 | 44 | 20 | 80 |
| 2 | 12 | 5 | 23 |
| 3 | 14 | 8 | 21 |
| 4 | 8 | 5 | 14 |
| 5 | 9 | 6 | 13 |
| 6 | 11 | 8 | 15 |
| 7 | 4 | 3 | 7 |
| 8 | 7 | 4 | 10 |
| 9 | 15 | 11 | 20 |
Example 42.12. Complementary Log-Log Model for Interval-Censored Survival Times
Often survival times are not observed more precisely than the interval (for instance, a day) within which the event occurred. Survival data of this form are known as grouped or interval-censored data. A discrete analogue of the continuous proportional hazards model (Prentice and Gloeckler 1978; Allison 1982) is used to investigate the relationship between these survival times and a set of explanatory variables.
Suppose T i is the discrete survival time variable of the i th subject with covariates x i . The discrete-time hazard rate » it is defined as
Using elementary properties of conditional probabilities, it can be shown that
Suppose t i is the observed survival time of the i th subject. Suppose i = 1 if T i = t i is an event time and 0 otherwise . The likelihood for the grouped survival data is given by
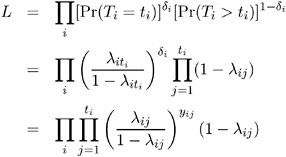
where y ij = 1 if the i th subject experienced an event at time T i = j and 0 otherwise.
Note that the likelihood L for the grouped survival data is the same as the likelihood of a binary response model with event probabilities » ij . If the data are generated by a continuous-time proportional hazards model, Prentice and Gloeckler (1978) have shown that
where the coefficient vector ² is identical to that of the continuous-time proportional hazards model, and ± j is a constant related to the conditional survival probability in the interval defined by T i = j at x i = . The grouped data survival model is therefore equivalent to the binary response model with complementary log-log link function. To fit the grouped survival model using PROC LOGISTIC, you must treat each discrete time unit for each subject as a separate observation. For each of these observations, the response is dichotomous, corresponding to whether or not the subject died in the time unit.
Consider a study of the effect of insecticide on flour-beetles. Four different concentrations of an insecticide were sprayed on separate groups of flour-beetles. The numbers of male and female flour-beetles dying in successive intervals were saved in the data set beetles .
data beetles(keep=time sex conc freq); input time m20 f20 m32 f32 m50 f50 m80 f80; conc=.20; freq= m20; sex=1; output; freq= f20; sex=2; output; conc=.32; freq= m32; sex=1; output; freq= f32; sex=2; output; conc=.50; freq= m50; sex=1; output; freq= f50; sex=2; output; conc=.80; freq= m80; sex=1; output; freq= f80; sex=2; output; datalines; 1 3 0 7 1 5 0 4 2 2 11 2 10 5 8 4 10 7 3 10 4 11 11 11 6 8 15 4 7 8 16 10 15 6 14 9 5 4 9 3 5 4 3 8 3 6 3 3 2 1 2 1 2 4 7 2 0 1 0 1 1 1 1 8 1 0 0 1 1 4 0 1 9 0 0 1 1 0 0 0 0 10 0 0 0 0 0 0 1 1 11 0 0 0 0 1 1 0 0 12 1 0 0 0 0 1 0 0 13 1 0 0 0 0 1 0 0 14 101 126 19 47 7 17 2 4 ;
The data set beetles contains four variables: time , sex , conc , and freq . time represents the interval death time; for example, time =2 is the interval between day 1 and day 2. Insects surviving the duration (13 days) of the experiment are given a time value of 14. The variable sex represents the sex of the insects (1=male, 2=female), conc represents the concentration of the insecticide (mg/cm 2 ), and freq represents the frequency of the observations.
To use PROC LOGISTIC with the grouped survival data, you must expand the data so that each beetle has a separate record for each day of survival. A beetle that died in the third day ( time =3) would contribute three observations to the analysis, one for each day it was alive at the beginning of the day. A beetle that survives the 13-day duration of the experiment ( time =14) would contribute 13 observations.
A new data set days that contains the beetle-day observations is created from the data set beetles . In addition to the variables sex , conc and freq , the data set contains an outcome variable y and 13 indicator variables day1 , day2 , , day13 . y has a value of 1 if the observation corresponds to the day that the beetle died and has a value of 0 otherwise. An observation for the first day will have a value of 1 for day1 and a value of 0 for day2 “ day13 ; an observation for the second day will have a value of 1 for day2 and a value of 0 for day1 and day2 “ day13 . For instance, Output 42.12.1 shows an observation in the beetles data set with time =3, and Output 42.12.2 shows the corresponding beetle-day observations in the data set days .
| |
Obs time conc freq sex 17 3 0.2 10 1
| |
| |
d d d d t c f d d d d d d d d d a a a a O i o r s d a a a a a a a a a y y y y b m n e e a y y y y y y y y y 1 1 1 1 s e c q x y y 1 2 3 4 5 6 7 8 9 0 1 2 3 25 3 0.2 10 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 26 3 0.2 10 1 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 27 3 0.2 10 1 3 1 0 0 1 0 0 0 0 0 0 0 0 0 0
| |
data days; retain day1-day13 0; array dd[13] day1-day13; set beetles; if time = 14 then do day=1 to 13; y=0; dd[day]=1; output; dd[day]=0; end; else do day=1 to time; if day=time then y=1; else y=0; dd[day]=1; output; dd[day]=0; end;
The following SAS statements invoke PROC LOGISTIC to fit a complementary log-log model for binary data with response variable Y and explanatory variables day1 “ day13 , sex , and conc . Specifying the EVENT= option ensures that the event ( y =1) probability is modeled. The coefficients of day1 “ day13 can be used to estimate the baseline survival function. The NOINT option is specified to prevent any redundancy in estimating the coefficients of day1 “ day13 . The Newton-Raphson algorithm is used for the maximum likelihood estimation of the parameters.
proc logistic data=days outest=est1; model y(event='1')= day1-day13 sex conc / noint link=cloglog technique=newton; freq freq; run;
Results of the model fit are given in Output 42.12.3. Both sex and conc are statistically significant for the survival of beetles sprayed by the insecticide. Female beetles are more resilient to the chemical than male beetles, and increased concentration increases the effectiveness of the insecticide.
| |
The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi Square Pr > ChiSq day1 1 3.9314 0.2934 179.5602 <.0001 day2 1 2.8751 0.2412 142.0596 <.0001 day3 1 2.3985 0.2299 108.8833 <.0001 day4 1 1.9953 0.2239 79.3960 <.0001 day5 1 2.4920 0.2515 98.1470 <.0001 day6 1 3.1060 0.3037 104.5799 <.0001 day7 1 3.9704 0.4230 88.1107 <.0001 day8 1 3.7917 0.4007 89.5233 <.0001 day9 1 5.1540 0.7316 49.6329 <.0001 day10 1 5.1350 0.7315 49.2805 <.0001 day11 1 5.1131 0.7313 48.8834 <.0001 day12 1 5.1029 0.7313 48.6920 <.0001 day13 1 5.0951 0.7313 48.5467 <.0001 sex 1 0.5651 0.1141 24.5477 <.0001 conc 1 3.0918 0.2288 182.5665 <.0001
| |
The coefficients of day1 “ day13 are the maximum likelihood estimates of ± 1 , , ± 13 , respectively. The baseline survivor function S ( t ) is estimated by
and the survivor function for a given covariate pattern ( sex = x 1 and conc = x 2 )is estimated by
The following statements compute the survivor curves for male and female flour-beetles exposed to the insecticide of concentrations 0.20 mg/cm 2 and 0.80 mg/cm 2 . The GPLOT procedure in SAS/GRAPH software is used to plot the survival curves. Instead of plotting them as step functions, the SPLINE option is used to smooth the curves. These smoothed survival curves are displayed in Output 42.12.4.
| |
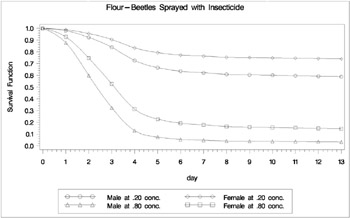
| |
legend1 label=none frame cframe=white cborder=black position=center value=(justify=center); run; axis1 label=(angle=90 'Survival Function'); proc gplot data=one; plot (s_m20 s_f20 s_m80 s_f80) * day / overlay legend=legend1 vaxis=axis1; symbol1 v=circle i=spline c=black height=.8; symbol2 v=diamond i=spline c=black height=.8; symbol3 v=triangle i=spline c=black height=.8; symbol4 v=square i=spline c=black height=.8; run;
The probability of survival is displayed on the vertical axis. Notice that most of the insecticide effect occurs by day 6 for both the high and low concentrations.
Example 42.13. Scoring Data Sets with the SCORE Statement
This example first illustrates the syntax used for scoring data sets, then uses a previously scored data set to score a new data set. A generalized logit model is fitto the remote-sensing data set used in Example 25.4 on page 1231 of Chapter 25, The DISCRIM Procedure, to illustrate discrimination and classification methods. The response variable is Crop and the prognostic factors are x1 through x4 .
data Crops; length Crop $ 10; infile datalines truncover; input Crop $ @@; do i=1 to 3; input x1-x4 @@; if (x1 ^= .) then output; end; input; datalines; Corn 16 27 31 33 15 23 30 30 16 27 27 26 Corn 18 20 25 23 15 15 31 32 15 32 32 15 Corn 12 15 16 73 Soybeans 20 23 23 25 24 24 25 32 21 25 23 24 Soybeans 27 45 24 12 12 13 15 42 22 32 31 43 Cotton 31 32 33 34 29 24 26 28 34 32 28 45 Cotton 26 25 23 24 53 48 75 26 34 35 25 78 Sugarbeets 22 23 25 42 25 25 24 26 34 25 16 52 Sugarbeets 54 23 21 54 25 43 32 15 26 54 2 54 Clover 12 45 32 54 24 58 25 34 87 54 61 21 Clover 51 31 31 16 96 48 54 62 31 31 11 11 Clover 56 13 13 71 32 13 27 32 36 26 54 32 Clover 53 08 06 54 32 32 62 16 ;
You can specify a SCORE statement to score the Crops data using the fitted model. The data together with the predicted values are saved into the data set Score1 .
proc logistic data=Crops; model Crop=x1-x4 / link=glogit; score out=Score1; run;
The OUTMODEL= option saves the fitted model information in a data set. In the following statements, the model is again fit, the data and the predicted values are saved into the data set Score2 , and the model information is saved in the permanent SAS data set sasuser.CropModel .
proc logistic data=Crops outmodel=sasuser.CropModel; model Crop=x1-x4 / link=glogit; score data=Crops out=Score2; run;
To score data without refitting the model, specify the INMODEL= option to identify a previously saved SAS data set of model information. In the following statements, the model is read from the sasuser.CropModel data set, and the data and the predicted values are saved into the data set Score3 .
proc logistic inmodel=sasuser.CropModel; score data=Crops out=Score3; run;
To set prior probabilities on the responses, specify the PRIOR= option to identify a SAS data set containing the response levels and their priors . In the following statements, the Prior data set contains the values of the response variable (because this example uses single-trial MODEL syntax) and a _PRIOR_ variable containing values proportional to the default priors. The model is fit, then the data and the predicted values are saved into the data set Score4 .
data Prior; input Crop $ 1-10 _PRIOR_; datalines; Clover 11 Corn 7 Cotton 6 Soybeans 6 Sugarbeets 6 ; proc logistic inmodel=sasuser.CropModel; score data=Crops prior=prior out=Score4; run;
The data sets Score1 , Score2 , Score3 , and Score4 are identical.
The following statements display the results of scoring the Crops data set in Output 42.13.1.
| |
The FREQ Procedure Table of F_Crop by I_Crop F_Crop(From: Crop) I_Crop(Into: Crop) Frequency Row Pct Clover Corn Cotton Soybeans Sugarbee Total ts -----------+--------+--------+--------+--------+--------+ Clover 6 0 2 2 1 11 54.55 0.00 18.18 18.18 9.09 -----------+--------+--------+--------+--------+--------+ Corn 0 7 0 0 0 7 0.00 100.00 0.00 0.00 0.00 -----------+--------+--------+--------+--------+--------+ Cotton 4 0 1 1 0 6 66.67 0.00 16.67 16.67 0.00 -----------+--------+--------+--------+--------+--------+ Soybeans 1 1 1 3 0 6 16.67 16.67 16.67 50.00 0.00 -----------+--------+--------+--------+--------+--------+ Sugarbeets 2 0 0 2 2 6 33.33 0.00 0.00 33.33 33.33 -----------+--------+--------+--------+--------+--------+ Total 13 8 4 8 3 36
| |
proc freq data=Score1; table F_Crop*I_Crop / nocol nocum nopercent; run;
Now the previously fit data set sasuser.CropModel is used to score the new observations in the Test data set. The following statements save the results of scoring the test data in the ScoredTest data set and produces Output 42.13.2.
| |
Predicted Predicted Into: Probability: Probability: From: Crop Crop Crop=Clover Crop=Corn Corn Corn 0.00342 0.90067 Soybeans Soybeans 0.04801 0.03157 Cotton Clover 0.43180 0.00015 Sugarbeets Clover 0.66681 0.00000 Clover Cotton 0.41301 0.13386 Predicted Predicted Predicted Probability: Probability: Probability: Crop=Cotton Crop=Soybeans Crop=Sugarbeets 0.00500 0.08675 0.00416 0.02865 0.82933 0.06243 0.21267 0.07623 0.27914 0.17364 0.00000 0.15955 0.43649 0.00033 0.01631
| |
data Test; input Crop $ 1-10 x1-x4; datalines; Corn 16 27 31 33 Soybeans 21 25 23 24 Cotton 29 24 26 28 Sugarbeets 54 23 21 54 Clover 32 32 62 16 ; proc logistic noprint inmodel=sasuser.CropModel; score data=Test out=ScoredTest; proc print data=ScoredTest label noobs; var F_Crop I_Crop P_Clover P_Corn P_Cotton P_Soybeans P_Sugarbeets; run;
- ERP Systems Impact on Organizations
- ERP System Acquisition: A Process Model and Results From an Austrian Survey
- The Second Wave ERP Market: An Australian Viewpoint
- Enterprise Application Integration: New Solutions for a Solved Problem or a Challenging Research Field?
- Context Management of ERP Processes in Virtual Communities