Chapter 6_ The Peripheral Vascular System | Cardiovascular Physiology: Mosby Physiology Monograph Series, 9e (Mosbys Physiology Monograph)

Print Close Window

Note: Large images and tables on this page may necessitate printing in landscape mode.

Copyright 2006 The McGraw-Hill Companies. All rights reserved.

Lange Cardiovascular Physiology > Chapter 6. The Peripheral Vascular System >

Objectives

The student understands the basic principles of cardiovascular transport and its role in maintaining homeostasis:

Defines convective transport and diffusion and lists the factors that determine the rate of each.
Given data, uses the Fick principle to calculate the rate of removal of a solute from blood as it passes through an organ.
Describes how capillary wall permeability to a solute is related to the size and lipid solubility of the solute.
Lists the factors that influence transcapillary fluid movement and, given data, predicts the direction of transcapillary fluid movement.
Describes the lymphatic vessel system and its role in preventing fluid accumulation in the interstitial space.

The student understands the physical factors that regulate blood flow through the various components of the vasculature:

Given data, calculates the vascular resistances of networks of vessels arranged in parallel and in series.
Describes differences in the blood flow velocity in the various segments and how these differences are related to their total cross-sectional area.
Describes laminar and turbulent flow patterns and the origin of flow sounds in the cardiovascular system.
Identifies the approximate percentage of the total blood volume that is contained in the various vascular segments in the systemic circulation.
Defines peripheral venous pool and central venous pool.
Describes the pressure changes that occur as blood flows through a vascular bed and relates them to the vascular resistance of the various vascular segments.
States how the resistance of each consecutive vascular segment contributes to an organ's overall vascular resistance and, given data, calculates the overall resistance.
Defines total peripheral resistance (systemic vascular resistance) and states the relationship between it and the vascular resistance of each systemic organ.
Defines vascular compliance and states how the volume-pressure curves for arteries and veins differ.
Predicts what will happen to venous volume when venous smooth muscle contracts or when venous transmural pressure increases.
Describes the role of arterial compliance in storing energy for blood circulation.
Describes the auscultation technique of determining arterial systolic and diastolic pressures.
Identifies the physical bases of the Korotkoff sounds.
Indicates the relationship between arterial pressure, cardiac output, and total peripheral resistance and predicts how arterial pressure will be altered when cardiac output and/or total peripheral resistance change.
Given arterial systolic and diastolic pressures, estimates mean arterial pressure.
Indicates the relationship between pulse pressure, stroke volume, and arterial compliance and predicts how pulse pressure will be changed by changes in stroke volume, or arterial compliance.
Describes how arterial compliance changes with age and how this affects arterial pulse pressure.

The Peripheral Vascular System: Introduction

An overview of the vascular system was presented in Chapter 1. Many more details about vascular design and operation are presented in this chapter. Be careful not to let these details detract from understanding the overall picture presented earlier.

Cardiovascular Transport

The Fick Principle

Substances are carried between organs within the cardiovascular system by the process of convective transport, the simple process of being swept along with the flow of the blood in which they are contained. The rate at which a substance (X) is transported by this process depends solely on the concentration of the substance in the blood and the blood flow rate.

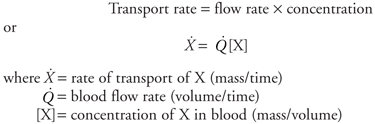
It is evident from the preceding equation that only two methods are available for altering the rate at which a substance is carried to an organ: (1) a change in the blood flow rate through the organ or (2) a change in the arterial blood concentration of the substance. The preceding equation might be used, for example, to calculate how much oxygen is carried to a certain skeletal muscle each minute. Note, however, that this calculation would not indicate whether the muscle actually used the oxygen carried to it.

One can extend the convective transport principle to determine a tissue's rate of utilization (or production) of a substance by simultaneously considering the transport rate of the substance to and from the tissue. The relationship that results is referred to as the Fick principle (Adolf Fick, a German physician, 1829 1901) and may be formally stated as follows: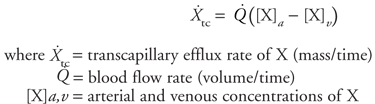

The Fick principle essentially says that the amount of a substance that goes into an organ in a given period of time ([X]_a) minus the amount that comes out ([X]_v) must equal the tissue utilization rate of that substance. (If the tissue is producing substance X, then the above equation will yield a negative utilization rate.)

Recall that one method for determining cardiac output described in Chapter 3 used the Fick principle to calculate the blood flow rate through the systemic circulation. In that case, the known variables included the systemic tissue oxygen consumption rate and the concentrations of oxygen in arterial blood and mixed venous blood. The above equation was rearranged to solve for the blood flow rate ().

Transcapillary Solute Diffusion

Capillaries act as efficient exchange sites where most substances cross the capillary walls simply by passively diffusing from regions of high concentration to regions of low concentration.¹ As in any diffusion situation, there are four factors that determine the diffusion rate of a substance between the blood and the interstitial fluid: (1) the concentration difference, (2) the surface area for exchange, (3) the diffusion distance, and (4) the permeability of the capillary wall to the diffusing substance.²

Capillary beds allow huge amounts of materials to enter and leave blood because they maximize the area across which exchange can occur while minimizing the distance over which the diffusing substances must travel. Capillaries are extremely fine vessels with a lumen (inside) diameter of about 5 m, a wall thickness of approximately 1 m, and an average length of perhaps 0.5 mm. (For comparison, a human hair is roughly 100 m in diameter.) Capillaries are distributed in incredible numbers in organs and communicate intimately with all regions of the interstitial space. It is estimated that there are about 10¹⁰ capillaries in the systemic organs with a collective surface area of about 100 square meters. That is roughly the area of one player's side of a singles tennis court. Recall from Chapter 1 that no cell is more than about 10 m (less than 1/10th the thickness of paper) from a capillary. Diffusion is a tremendously powerful mechanism for material exchange when operating over such a short distance and through such a large area. We are far from being able to duplicate in an artificial lung or kidney, for example the favorable geometry for diffusional exchange that exists in our own tissues.

As diagramed in Figure 6 1, the capillary wall itself consists of only a single thickness of endothelial cells joined to form a tube. The ease with which a particular solute crosses the capillary wall is expressed in a parameter called its capillary permeability. Permeability takes into account all the factors (diffusion coefficient, diffusion distance, and surface area) except concentration difference that affect the rate at which a solute crosses the capillary wall.

Careful experimental studies on how rapidly different substances cross capillary walls indicate that two fundamentally distinct pathways exist for transcapillary exchange. Lipid-soluble substances, such as the gases oxygen and carbon dioxide, cross the capillary wall easily. Because the lipid endothelial cell plasma membranes are not a significant diffusion barrier for lipid-soluble substances, trans-capillary movement of these substances can occur through the entire capillary surface area.

The capillary permeability to small polar particles such as sodium and potassium ions is about 10,000-fold less than that for oxygen. Nevertheless, the capillary permeability to small ions is several orders of magnitude higher than the permeability that would be expected if the ions were forced to move through the lipid plasma membranes. It is therefore postulated that capillaries are somehow perforated at intervals with water-filled channels or pores.³ Calculations from diffusion data indicate that the collective cross-sectional area of the pores relative to the total capillary surface area varies greatly between capillaries in different organs. Brain capillaries appear to be very tight (have few pores), whereas capillaries in the kidney and fluid-producing glands are much more leaky. On the average, however, pores constitute only a very small fraction of total capillary surface area perhaps 0.01%. This area is, nevertheless, sufficient to allow very rapid equilibration of small water-soluble substances between the plasma and interstitial fluids of most organs. Thus, the concentrations of inorganic ions measured in a plasma sample can be taken to indicate their concentrations throughout the entire extracellular space.

An effective maximum diameter of about 40 has been assigned to individual pores because substances with molecular diameters larger than this essentially do not cross capillary walls.⁴ Thus, albumin and other proteins in the plasma are normally confined to the plasma space.⁵

¹ Evidence indicates that the capillary endothelial cells can metabolize or produce certain substances. In these special cases, the capillary wall cannot be considered as a passive barrier between the intravascular and interstitial compartments.

² These factors are combined in an equation (Fick's first law of diffusion) which describes the rate of diffusion (_d) of a substance X across a barrier: _d = DA [X]/L, where D, A, [X], and L represent the diffusion coefficient, surface area, concentration difference, and diffusion distance, respectively.

³ Pores, as such, are not readily apparent in electron micrographs of capillary endothelial cells. Most believe the pores are really clefts in the junctions between endothelial cells.

⁴ The precise mechanism responsible for this size-selectivity remains controversial. It may stem from the actual physical dimensions of the "pores," or it may represent the filtering properties of a fiber matrix that either covers or fills the pores.

⁵ In reality, macromolecules do cross capillary walls ever so slowly by a pinocytotic mechanism sometimes referred to as the "large pore" system. Even with this special system, the capillary protein permeability is still about 1000-fold less than either sodium or glucose permeability.

Transcapillary Fluid Movement

In addition to providing a diffusion pathway for polar molecules, the water-filled channels that traverse capillary walls permit fluid flow through the capillary wall. Net shifts of fluid between the capillary and interstitial compartments are important for a host of physiological functions, including the maintenance of circulating blood volume, intestinal fluid absorption, tissue edema formation, and saliva, sweat, and urine production. Net fluid movement out of capillaries is referred to as filtration, and fluid movement into capillaries is called reabsorption.

Fluid flows through transcapillary channels in response to pressure differences between the interstitial and intracapillary fluids according to the basic flow equation. However, both hydrostatic and osmotic pressures influence transcapillary fluid movement. How hydrostatic pressure provides the driving force for causing blood flow along vessels has been discussed previously. The hydrostatic pressure inside capillaries, P_c, is about 25 mmHg and is the driving force that causes blood to return to the right heart from the capillaries of systemic organs. In addition, however, the 25-mmHg hydrostatic intracapillary pressure tends to cause fluid to flow through the transcapillary pores into the interstitium where the hydrostatic pressure (P_i) is near 0 mmHg. Thus, there is normally a large hydrostatic pressure difference favoring fluid filtration across the capillary wall. Our entire plasma volume would soon be in the interstitium if there were not some counteracting force tending to draw fluid into the capillaries. The balancing force is an osmotic pressure that arises from the fact that plasma has a higher protein concentration than does interstitial fluid.

Recall that water always tends to move from regions of low to regions of high total solute concentration in establishing osmotic equilibrium. Also recall that osmotic forces are quantitatively expressed in terms of osmotic pressure. The osmotic pressure of a given solution is defined as the hydrostatic pressure necessary to prevent osmotic water movement into the test solution when it is exposed to pure water across a membrane permeable only to water. The total osmotic pressure of a solution is proportional to the total number of solute particles in the solution. Plasma, for example, has a total osmotic pressure of about 5000 mmHg nearly all of which is attributable to dissolved mineral salts such as NaCl and KCl. As discussed, the capillary permeability to small ions is quite high. Their concentrations in plasma and interstitial fluid are very nearly equal and, consequently, they do not affect transcapillary fluid movement. However, there is a small but important difference in the osmotic pressures of plasma and interstitial fluid that is due to the presence of albumin and other proteins in the plasma, which are normally absent from the interstitial fluid. A special term, oncotic pressure, is used to denote that portion of a solution's total osmotic pressure that is due to particles that do not move freely across capillaries.⁶ Because of the plasma proteins, the oncotic pressure of plasma (_c) is about 25 mmHg. Due to the absence of proteins, the oncotic pressure of the interstitial fluid (_i) is near 0 mmHg. Thus, there is normally a large osmotic force for fluid reabsorption into capillaries. The forces that influence transcapillary fluid movement are summarized on the left side of Figure 6 2.

The relationship among the factors that influence transcapillary fluid movement, known as the Starling hypothesis,⁷ can be expressed by the equation:

Fluid balance within a tissue (the absence of net transcapillary water movement) occurs when the bracketed term in this equation is zero. This equilibrium may be upset by alterations in any of the four pressure terms. The pressure imbalances that cause capillary filtration and reabsorption are indicated on the right side of Figure 6 2.

In most tissues, rapid net filtration of fluid is abnormal and causes tissue swelling as a result of excess fluid in the interstitial space (edema). For example, a substance called histamine is often released in damaged tissue. One of the actions of histamine is to increase capillary permeability to the extent that proteins leak into the interstitium. Net filtration and edema accompany histamine release, in part because the oncotic pressure difference (_c _i) is reduced below normal.

Transcapillary fluid filtration is not always detrimental. Indeed, fluid-producing organs such as salivary glands and kidneys utilize high intracapillary hydrostatic pressure to produce continual net filtration. Moreover, in certain abnormal situations, such as severe loss of blood volume through hemorrhage, the net fluid reabsorption accompanying diminished intracapillary hydrostatic pressure helps restore the volume of circulating fluid.

⁶ This osmotic force is also called "colloid osmotic pressure."

⁷ After the British physiologist Ernest Starling (1866 1927).

Lymphatic System

Despite the extremely low capillary permeability to proteins, these molecules as well as other large particles such as long-chain fatty acids and bacteria find their way into the interstitial space. If such particles are allowed to accumulate in the interstitial space, filtration forces will ultimately exceed reabsorption forces and edema will result. The lymphatic system represents a pathway by which large molecules reenter the circulating blood.

The lymphatic system begins in the tissues with blind-end lymphatic capillaries that are roughly equivalent in size to but less numerous than regular capillaries. These capillaries are very porous and easily collect large particles accompanied by interstitial fluid. This fluid, called lymph, moves through the converging lymphatic vessels, is filtered through lymph nodes where bacteria and particulate matter are removed, and reenters the circulatory system near the point where the blood enters the right heart.

Flow of lymph from the tissues toward the entry point into the circulatory system is promoted by two factors: (1) increases in tissue interstitial pressure (due to fluid accumulation or to movement of surrounding tissue) and (2) contractions of the lymphatic vessels themselves. Valves located in these vessels also prevent backward flow.

Roughly 2.5 L of lymphatic fluid enters the cardiovascular system each day. In the steady state, this indicates a total body net transcapillary fluid filtration rate of 2.5 L per day. When compared with the total amount of blood that circulates each day (about 7000 L), this may seem like an insignificant amount of net capillary fluid leakage. However, lymphatic blockage is a very serious problem and is accompanied by severe swelling. Thus, the lymphatics play a critical role in keeping the interstitial protein concentration low and in removing excess capillary filtrate from the tissues.

Basic Vascular Function

Resistance & Flow in Networks of Vessels

In Chapter 1, it was asserted that the basic flow equation ( = P/R) may be applied to networks of tubes as well as to individual tubes. The reason is that any network of resistances, however complex, can always be reduced to a single "equivalent" resistor that relates the total flow through the network to the pressure difference across the network. Of course one way of finding the overall resistance of a network is to perform an experiment to see how much flow goes through it for a given pressure difference between its inlet and outlet. Another approach to finding the overall resistance of a network is to calculate it from a knowledge of the resistances of the individual elements in the network and how they are connected. To do so, one needs to apply the parallel and series resistance formulas presented below. These formulas may look familiar because they are analogous to those by which networks of electrical resistances are analyzed with Ohm's law (I = V/R).

When vessels with individual resistances R₁, R₂, . . . , R_n are connected in series, the overall resistance of the network is given by the following formula: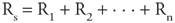

Figure 6 3A shows an example of three vessels connected in series between some region where the pressure is P_i and another region with a lower pressure P_o, so that the total pressure difference across the network, P, is equal to P_i P_o. By the series resistance equation, the total resistance across this network (R_s) is equal to R₁ + R₂ + R₃. By the basic flow equation, the flow through the network () is equal to P/R_s. It should be intuitively obvious that () is the flow (volume/time) through each of the elements in the series as indicated in Figure 6 3B. [Fluid particles may move with different velocities (distance/time) in different elements of a series network, but the volume that passes through each element in a minute must be identical.]

As shown in Figure 6 3C, a portion of the total pressure drop across the network occurs within each element of the series. The pressure drop across any element in the series can be calculated by applying the basic flow equation to that element, eg, P₁ = R₁. Note that the largest portion of the overall pressure drop will occur across the element in the series with the largest resistance to flow (R₂ in Figure 6 3).

As indicated in Figure 6 4, when several tubes with individual resistances R₁, R₂, . . . , R_n are brought together to form a parallel network of vessels, one can calculate a single overall resistance for the parallel network R_p according to the following formula: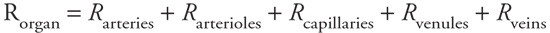

The total flow through a parallel network is determined by P/R_p. As the preceding equation implies, the overall resistance of any parallel network will always be less than that of any of the elements in the network. (In the special case where the individual elements that form the network have identical resistances R_x, the overall resistance of the network is equal to the resistance of an individual element divided by the number of n of parallel elements in the network: R_p = R_x/n.) In general, the more parallel elements that occur in the network, the lower the overall resistance of the network. Thus, for example, a capillary bed that consists of many individual capillary vessels in parallel can have a very low overall resistance to flow even though the resistance of a single capillary is relatively high.

As indicated in Figure 6 4, the basic flow equation may be applied to any single element in the network or to the network as a whole. For example, the flow through only the first element of the network (₁) is given by ₁ = P/R₁, whereas the flow through the entire parallel network is given by _p = P/R_p.

The series and parallel resistance equations may be used alternately to analyze resistance networks of great complexity. For example, any or all of the series resistances shown in Figure 6 3 could actually represent the calculated overall resistance of many vessels arranged in parallel.

Peripheral Blood Flow Velocities

It is important to make the distinction between blood flow (volume/time) and blood flow velocity (distance/time) in the peripheral vascular system. Consider the analogy of a stream whose water moves with greater velocity through a shallow rapids than it does through an adjacent deep pool. The volume of water passing through the pool in a day (volume/time = flow), however, must equal that passing through the rapids in the same day. In such a series arrangement, the flow is the same at all points along the channel but the flow velocity varies inversely with the local cross-sectional area. The situation is the same in the peripheral vasculature, where blood flows most rapidly in the region with the smallest total cross-sectional area (the aorta) and most slowly in the region with the largest total cross-sectional area (the capillary beds). Regardless of the differences in velocity, when the cardiac output (flow into the aorta) is 5 L/min, the flow through the systemic capillaries (or arterioles, or venules) is also 5 L/min. The changes in flow velocity that occur as blood passes through the peripheral vascular system are shown in the top trace of Figure 6 5. These are a direct consequence of the variations in total cross-sectional area that were indicated in Figure 1 8.

Blood normally flows through all vessels in the cardiovascular system in an orderly streamlined manner called laminar flow. With laminar flow, there is a parabolic velocity profile across the tube as shown on the left side of Figure 6 6. Velocity is fastest along the central axis of the tube and falls to zero at the wall. The concentric layers of fluid with different velocities slip smoothly over one another. Little mixing occurs between fluid layers so that individual particles move in straight streamlines parallel to the axis of the flow. Laminar flow is very efficient because little energy is wasted on anything but producing forward fluid motion.

Because blood is a viscous fluid, its movement through a vessel exerts a shear stress on the walls of the vessel. This is a force that wants to drag the inside surface (the endothelial cell layer) of the vessel along with the flow. With laminar flow, the shear stress on the wall of a vessel is proportional to the rate of flow through it.⁸ The endothelial cells that line a vessel are able to sense (and possibly respond to) changes in the rate of blood flow through the vessel by detecting changes in the shear stress on them. Shear stress may also be an important factor in certain pathological situations. For example, atherosclerotic plaques tend to form preferentially near branches off large arteries where, for complex hemodynamic reasons beyond the scope of this text, high shear stresses exist.

When blood is forced to move with too high a velocity through a narrow opening, the normal laminar flow pattern may break down into the turbulent flow pattern shown on the right side of Figure 6 6.⁹ With turbulent flow, there is much internal mixing and friction. When the flow within a vessel is turbulent, the vessel's resistance to flow is significantly higher than that predicted from the Poiseuille equation given in Chapter 1. Turbulent flow also generates sound, which can be heard with the aid of a stethoscope. Cardiac murmurs, for example, are manifestations of turbulent flow patterns generated by cardiac valve abnormalities. Detection of sounds from peripheral arteries (bruits) is abnormal and usually indicates significant pathological reduction of a large vessel's cross-sectional area.

⁸ With pure laminar flow of a homogeneous fluid in a uniform smooth round tube, the shear stress (force/surface area _s) on the wall is a function of fluid viscosity (), flow (volume/time, ), and the inside radius of the tube (r_i) as follows: _s = 4/r_i³.

⁹ Turbulence occurs when a parameter called the Reynolds number (R_e) exceeds a value of 2000. R_e = 4Q/d_i, where = fluid density, = flow (volume-time), = fluid viscosity, and d_i = inside diameter.

Peripheral Blood Volumes

The second trace in Figure 6 5 shows the approximate percentage of the total circulating blood volume that is contained in the different vascular regions of the systemic organs at any instant of time. (Approximately 20% of the total volume is contained in the pulmonary system and the heart chambers and is not accounted for in this figure.) Note that most of the circulating blood is contained within the veins of the systemic organs. This diffuse but large blood reservoir is often referred to as the peripheral venous pool. A second but smaller reservoir of venous blood, called the central venous pool, is contained in the great veins of the thorax and the right atrium. When peripheral veins constrict, blood is displaced from the peripheral venous pool and enters the central pool. An increase in the central venous volume, and thus pressure, enhances cardiac filling, which in turn augments stroke volume according to the Frank-Starling law of the heart. This is an extremely important mechanism of cardiovascular regulation and will be discussed in greater detail in Chapter 8.

Peripheral Blood Pressures

Blood pressure decreases in the consecutive segments with the pattern shown in the third trace of Figure 6 5. Recall from Figure 3 1 that aortic pressure fluctuates between a systolic and diastolic value with each heartbeat, and the same is true throughout the arterial system. (For complex hemodynamic reasons, the difference between systolic and diastolic pressure actually increases with the distance from the heart in the large arteries.¹⁰) The average pressure in the arch of the aorta, however, is about 100 mmHg, and this mean arterial pressure falls by only a small amount within the arterial system.

A large pressure drop occurs in the arterioles, where the pulsatile nature of the pressure also nearly disappears. The average capillary pressure is approximately 25 mmHg. Pressure continues to decrease in the venules and veins as blood returns to the right heart. The central venous pressure (which is the filling pressure for the right heart) is normally very close to 0 mmHg.

¹⁰ A rigorous analysis of the dynamics of pulsatile fluid flow in tapered, branching, elastic tubes is required to explain such behavior. Pressure does not increase simultaneously throughout the arterial system with the onset of cardiac ejection. Rather, the pressure increase begins at the root of the aorta and travels outward from there. When this rapidly moving pressure wave encounters obstacles such as vessel bifurcations, reflected waves are generated which travel back toward the heart. These reflected waves can summate with and reinforce the oncoming wave in a manner somewhat analogous to the progressive cresting of surface waves as they impinge on a beach.

Peripheral Vascular Resistances

The bottom trace in Figure 6 5 indicates the relative resistance to flow that exists in each of the consecutive vascular regions. Recall from Chapter 1 that resistance, pressure difference, and flow are related by the basic flow equation = P/R. Because the flow () must be the same through each of the consecutive regions indicated in Figure 6 5, the pressure drop that occurs across each of these regions is a direct reflection of the resistance to flow within that region (see Figure 6 3). Thus, the large pressure drop occurring as blood moves through arterioles indicates that arterioles present a large resistance to flow. The mean pressure drops little in arteries because they have little resistance to flow. Similarly, the modest pressure drop that exists across capillaries is a reflection of the fact that the capillary bed has a modest resistance to flow when compared with that of the arteriolar bed. (Recall from Figure 6 4 that the capillary bed can have a low resistance to flow because it is a parallel network of a very large number of individual capillaries.)

Blood flow through many individual organs can vary over a 10-fold or greater range. Because mean arterial pressure is a relatively stable cardiovascular variable, large changes in an organ's blood flow are achieved by changes in its overall vascular resistance to blood flow. The consecutive vascular segments are arranged in series within an organ, and the overall vascular resistance of the organ must equal the sum of the resistances of its consecutive vascular segments: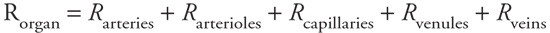

Because arterioles have such a large vascular resistance in comparison to the other vascular segments, the overall vascular resistance of any organ is determined to a very large extent by the resistance of its arterioles. Arteriolar resistance is, of course, strongly influenced by arteriolar radius (R is proportional to l/r⁴). Thus, the blood flow through an organ is primarily regulated by adjustments in the internal diameter of arterioles caused by contraction or relaxation of their muscular arteriolar walls.

When the arterioles of an organ change diameter, not only does the flow to the organ change but the manner in which the pressures drop within the organ is also modified. The effects of arteriolar dilation and constriction on the pressure profile within a vascular bed are illustrated in Figure 6 7. Arteriolar constriction causes a greater pressure drop across the arterioles, and this tends to increase the arterial pressure while it decreases the pressure in capillaries and veins. (The arterioles function somewhat like a dam; closing a dam s gates decreases the flow while increasing the level of the reservoir behind it and decreasing the level of its outflow stream.) Conversely, increased organ blood flow caused by arteriolar dilation is accompanied by decreased arterial pressure and increased capillary pressure. Because of the changes in capillary hydrostatic pressure, arteriolar constriction tends to cause transcapillary fluid reabsorption whereas arteriolar dilation tends to promote transcapillary fluid filtration.

Total Peripheral Resistance

The overall resistance to flow through the entire systemic circulation is called the total peripheral resistance. Because the systemic organs are generally arranged in parallel (Figure 1 2), the vascular resistance of each organ contributes to the total peripheral resistance according to the following parallel resistance equation:

As will be discussed later in this chapter, the total peripheral resistance is an important determinant of arterial blood pressure.

Elastic Properties of Arteries & Veins

As indicated earlier, arteries and veins contribute only a small portion to the overall resistance to flow through a vascular bed. Therefore, changes in their diameters have no significant effect on the blood flow through systemic organs. The elastic behavior of arteries and veins is, however, very important to overall cardiovascular function because they can act as reservoirs and substantial amounts of blood can be stored in them. Arteries or veins behave more like balloons with one pressure throughout rather than as resistive pipes with a flow-related pressure difference from end-to-end. Thus, think of an "arterial compartment" and a "venous compartment," each with an internal pressure that is related to the volume of blood within it at any instant and how elastic (stretchy) its walls are.

The elastic nature of a vascular region is characterized by a parameter called compliance (C) that describes how much its volume changes (V) in response to a given change in distending pressure (P): C = V/P. Distending pressure is the difference between the internal and external pressures on the vascular walls.

The volume-pressure curves for the systemic arterial and venous compartments are shown in Figure 6 8. It is immediately apparent from the disparate slopes of the curves in this figure that the elastic properties of arteries and veins are very different. For the arterial compartment, the V/P measured near a normal operating pressure of 100 mmHg indicates a compliance of about 2 mL/mmHg. By contrast, the venous pool has a compliance of over 100 mL/mmHg near its normal operating pressure of 5 to 10 mmHg.

Because veins are so compliant, even small changes in peripheral venous pressure can cause a significant amount of the circulating blood volume to shift into or out of the peripheral venous pool. Standing upright, for example, increases venous pressure in the lower extremities and promotes blood accumulation (pooling) in these vessels as might be represented by a shift from point A to point B in Figure 6 8. Fortunately, this process can be counteracted by active venous constriction. The dashed line in Figure 6 8 shows the venous volume-pressure relationship that exists when veins are constricted by activation of venous smooth muscle. In constricted veins, volume may be normal (point C) or even below normal (point D) despite higher than normal venous pressure. Peripheral venous constriction tends to increase peripheral venous pressure and shift blood out of the peripheral venous compartment.

The elasticity of arteries allows them to act as a reservoir on a beat-to-beat basis. Arteries play an important role in converting the pulsatile flow output of the heart into a steady flow through the vascular beds of systemic organs. During the early rapid phase of cardiac ejection, the arterial volume increases because blood is entering the aorta more rapidly than it is passing into systemic arterioles. Thus, part of the work the heart does in ejecting blood goes to stretching the elastic walls of arteries. Toward the end of systole and throughout diastole, arterial volume decreases because the flow out of arteries exceeds flow into the aorta. Previously stretched arterial walls recoil to shorter lengths, and in the process give up their stored potential energy. This reconverted energy is what actually does the work of propelling blood through the peripheral vascular beds during diastole. If the arteries were rigid tubes that could not store energy by expanding elastically, arterial pressure would fall immediately to zero with the termination of each cardiac ejection.

Measurement of Arterial Pressure

Recall that the systemic arterial pressure fluctuates with each heart cycle between a diastolic value (P_D) and a higher systolic value (P_S). Obtaining estimates of an individual's systolic and diastolic pressures is one of the most routine diagnostic techniques available to the physician. The basic principles of the auscultation technique used to measure blood pressure are described here with the aid of Figure 6 9.

An inflatable cuff is wrapped around the upper arm, and a device, such as a mercury manometer, is attached to monitor the pressure within the cuff. The cuff is initially inflated with air to a pressure (175 to 200 mmHg) that is well above normal systolic values. This pressure is transmitted from the flexible cuff into the upper arm tissues, where it causes all blood vessels to collapse. No blood flows into (or out of) the forearm as long as the cuff pressure is higher than the systolic arterial pressure. After the initial inflation, air is allowed to gradually "bleed" from the cuff so that the pressure within it falls slowly and steadily through the range of arterial pressure fluctuations. The moment the cuff pressure falls below the peak systolic arterial pressure, some blood is able to pass through the arteries beneath the cuff during the systolic phase of the cycle. This flow is intermittent and occurs only over a brief period of each heart cycle. Moreover, because it occurs through partially collapsed vessels beneath the cuff, the flow is turbulent rather than laminar. The intermittent periods of flow beneath the cuff produce tapping sounds, which can be detected with a stethoscope placed over the radial artery at the elbow. As indicated in Figure 6 9, sounds of varying character, known collectively as Korotkoff sounds, are heard whenever the cuff pressure is between the systolic and diastolic aortic pressures.

Because there is no blood flow and thus no sound when cuff pressure is higher than systolic arterial pressure, the highest cuff pressure at which tapping sounds are heard is taken as the systolic arterial pressure. When the cuff pressure falls below the diastolic pressure, blood flows through the vessels beneath the cuff without periodic interruption and again no sound is detected over the radial artery. The cuff pressure at which the sounds become muffled or disappear is taken as the diastolic arterial pressure. The Korotkoff sounds are more distinct when the cuff pressure is near the systolic arterial pressure than when it is near the diastolic pressure. Thus, consistency in determining diastolic pressure by auscultation requires concentration and experience.

Determinants of Arterial Pressure

Mean Arterial Pressure

Mean arterial pressure is a critically important cardiovascular variable because it is the average effective pressure that drives blood through the systemic organs. One of the most fundamental equations of cardiovascular physiology is that which indicates how mean arterial pressure (_A) is related to cardiac output (CO) and total peripheral resistance (TPR):

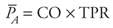
This equation is simply a rearrangement of the basic flow equation ( = P/R) applied to the entire systemic circulation with the single assumption that central venous pressure is approximately zero so that P = _A. Note that mean arterial pressure is influenced both by the heart (via cardiac output) and by the peripheral vasculature (via total peripheral resistance). All changes in mean arterial pressure result from changes in either cardiac output or total peripheral resistance.

Calculating the true value of mean arterial pressure requires mathematically averaging the arterial pressure waveform over one or more complete heart cycles. Most often, however, we know from auscultation only the systolic and diastolic pressures, yet wish to make some estimate of the mean arterial pressure. Mean arterial pressure necessarily falls between the systolic and diastolic pressures. A useful rule of thumb is that mean arterial pressure (_A) is approximately equal to diastolic pressure (P_D) plus one third of the difference between systolic and diastolic pressure (P_S P_D):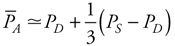

Arterial Pulse Pressure

The arterial pulse pressure (P_p) is defined simply as systolic pressure minus diastolic pressure: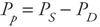

To be able to use pulse pressure to deduce something about how the cardiovascular system is operating, one must do more than just define it. It is important to understand what determines pulse pressure; ie, what causes it to be what it is and what can cause it to change. In a previous section of this chapter there was a brief discussion about how, as a consequence of the compliance of the arterial vessels, arterial pressure increases as arterial blood volume is expanded during cardiac ejection. The magnitude of the pressure increase (P) caused by an increase in arterial volume depends on how large the volume change (V) is and on how compliant (C_A) the arterial compartment is: P = V/C_A. If, for the moment, the fact that some blood leaves the arterial compartment during cardiac ejection is neglected, then the increase in arterial volume during each heartbeat is equal to the stroke volume (SV). Thus, pulse pressure is, to a first approximation, equal to stroke volume divided by arterial compliance: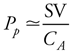

Arterial pulse pressure is about 40 mmHg in a normal resting young adult because stroke volume is about 80 mL and arterial compliance is about 2 mL/mmHg. Pulse pressure tends to increase with age in adults because of a decrease in arterial compliance ("hardening of the arteries"). Arterial volume-pressure curves for a 20-year-old and a 70-year-old are shown in Figure 6 10. The decrease in arterial compliance with age is indicated by the steeper curve for the 70-year-old (more P for a given V) than for the 20-year-old. Thus, a 70-year-old will necessarily have a larger pulse pressure for a given stroke volume than a 20-year-old. As indicated in Figure 6 10, the decrease in arterial compliance is sufficient to cause increased pulse pressure even though stroke volume tends to decrease with age.

Figure 6 10 also illustrates the fact that arterial blood volume and mean arterial pressure tend to increase with age. The increase in mean arterial pressure is not caused by the decreased arterial compliance, however, because compliance changes do not directly influence cardiac output or total peripheral resistance, which are the sole determinants of _A. Mean arterial pressure tends to increase with age because of an age-dependent increase in total peripheral resistance which is controlled primarily by arterioles, not arteries.

Arterial compliance also decreases with increasing mean arterial pressure as evidenced by the curvature of the volume-pressure relationships shown in Figure 6 10. Otherwise, arterial compliance is a relatively stable parameter. Thus, most acute changes in arterial pulse pressure are the result of changes in stroke volume.

The preceding equation for pulse pressure is a much simplified description of some very complex hemodynamic processes. It correctly identifies stroke volume and arterial compliance as the major determinants of arterial pulse pressure but is based on the assumption that no blood leaves the aorta during systolic ejection. Obviously this is not strictly correct. Furthermore, close examination of Figure 3 1 will reveal that peak systolic pressure is reached even before cardiac ejection is complete. It is therefore not surprising that several factors other than arterial compliance and stroke volume have minor influences on pulse pressure. For example, faster cardiac ejection caused by increased myocardial contractility tends to increase pulse pressure somewhat even if stroke volume remains constant. Changes in total peripheral resistance, however, have little or no effect on pulse pressure, because a change in total peripheral resistance causes parallel changes in both systolic and diastolic pressure.

A common misconception in cardiovascular physiology is that the systolic pressure alone or the diastolic pressure alone indicates the status of a specific cardiovascular variable. For example, high diastolic pressure is often taken to indicate high total peripheral resistance. This is not necessarily so since high diastolic pressure can exist with normal (or even reduced) total peripheral resistance if heart rate and cardiac output are high. Both systolic pressure and diastolic pressure are influenced by heart rate, stroke volume, total peripheral resistance, and C_A.¹¹ The student should not attempt to interpret systolic and diastolic pressure values independently. Interpretation is much more straightforward when the focus is on mean arterial pressure (_A = CO x TPR) and arterial pulse pressure (P_p SV/C_A). (See study question 14.)

¹¹ The equations presented in this and preceding chapters can be solved simultaneously to show that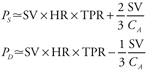

Key Concepts

Within the cardiovascular system, convection is used to transport substances between capillary beds and diffusion is used to transport substances between blood and tissue.

Water may move out of (filtration) or into (reabsorption) capillaries depending on the net balance of hydrostatic and osmotic forces across capillary walls.

Plasma proteins are responsible for the major osmotic force across capillary walls.

Lymphatic vessels serve to remove excess filtrate from tissues and keep interstitial protein concentration low.

Turbulent blood flow is abnormal and makes noise (murmurs and bruits).

Veins contain most of the total blood volume.

Arterioles contribute most to the resistance to flow through organs.

Arteriolar constriction tends to reduce flow through an organ and promote transcapillary fluid reabsorption within the organ.

Venous constriction is important for cardiac filling and the ability to cope with blood loss.

Because arteries are elastic, the intermittent flow from the heart is converted to continuous flow through capillaries.

Mean systemic arterial pressure is determined by the product of cardiac output and total peripheral resistance.

Changes in arterial pulse pressure reflect changes in stroke volume and/or the compliance of the arterial space.

Study Questions

6 1. Determine the rate of glucose uptake by an exercising skeletal muscle (

_m) from the following data:

Arterial blood glucose concentration, [G]_a = 50 mg per 100 mL

Muscle venous blood glucose concentration, [G]_v = 30 mg per 100 mL

Blood flow,

= 60 mL/min

6 2. Determine the direction of transcapillary fluid movement (

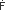) within a tissue, given the following data:

Capillary hydrostatic pressure, P_c = 28 mmHg

Plasma oncotic pressure,

_c = 24 mmHg

Tissue hydrostatic pressure, P_i = 4 mmHg

Tissue oncotic pressure,

_i = 0 mmHg

6 3. Which of the following conditions favor edema formation?

a. Lymphatic blockage

b. Thrombophlebitis (venous clot)

c. Decreased plasma protein concentration

d. Greatly increased capillary pore size

6 4. Assume that three vessels with identical dimensions are combined into a network of one vessel followed by a parallel combination of the other two and that a pressure (P_I) is applied to the inlet of the first vessel while a lower pressure (P_o) exists at the outlet of the parallel pair.

a. Find the overall resistance of the network (R_n) if the resistance of each vessel is equal to R_e.

b. Is the pressure (P_j) at the central junction of the network closer to P_i or P_o?

c. Use the basic flow equation to derive an equation that relates the pressure drop across the input vessel (P_i P_j) to the total pressure drop across the network (P_i P_o).

6 5. Given the following data, calculate an individual's total peripheral resistance (TPR):

Mean arterial pressure,

_A = 100 mmHg

Central venous pressure, P_CV = 0 mmHg

Cardiac output, CO = 6 L/min

6 6. The TPR to blood flow is greater than the resistance to flow through any of the systemic organs. True or false?

6 7. Other factors being equal, a decrease in the renal vascular resistance will increase TPR. True or false?

6 8. Constriction of arterioles in an organ promotes reabsorption of interstitial fluid from that organ. True or false?

6 9. Chronic elevation of arterial pressure requires that either cardiac output or TPR (or both) be chronically elevated. True or false?

6 10. Whenever cardiac output is increased, mean arterial pressure must also be increased. True or false?

6 11. Acute increases in arterial pulse pressure usually result from increases in stroke volume. True or false?

6 12. An increase in TPR increases diastolic pressure (P_D) more than systolic pressure (P_S). True or false?

6 13. Estimate the mean arterial pressure when the measured arterial pressure is 110/70 mmHg.

6 14. At rest the patient has a pulse rate of 70 beats per minute and an arterial blood pressure of 119/80 mmHg. During exercise on a treadmill, pulse rate is 140 beats per minute and blood pressure is 135/90 mmHg. Use this information to estimate the exercise-related changes in the following variables:

a. Stroke volume

b. Cardiac output

c. Total peripheral resistance (TPR)

See answers.