Statistical Background
Populations and Parameters
Usually, there is a clearly defined set of elements in which you are interested. This set of elements is called the universe , and a set of values associated with these elements is called a population of values. The statistical term population has nothing to do with people per se. A statistical population is a collection of values, not a collection of people. For example, a universe is all the students at a particular school, and there could be two populations of interest: one of height values and one of weight values. Or, a universe is the set of all widgets manufactured by a particular company, while the population of values could be the length of time each widget is used before it fails.
A population of values can be described in terms of its cumulative distribution function , which gives the proportion of the population less than or equal to each possible value. A discrete population can also be described by a probability function , which gives the proportion of the population equal to each possible value. A continuous population can often be described by a density function , which is the derivative of the cumulative distribution function. A density function can be approximated by a histogram that gives the proportion of the population lying within each of a series of intervals of values. A probability density function is like a histogram with an infinite number of infinitely small intervals.
In technical literature, when the term distribution is used without qualification, it generally refers to the cumulative distribution function. In informal writing, distribution sometimes means the density function instead. Often the word distribution is used simply to refer to an abstract population of values rather than some concrete population. Thus, the statistical literature refers to many types of abstract distributions, such as normal distributions, exponential distributions, Cauchy distributions, and so on. When a phrase such as normal distribution is used, it frequently does not matter whether the cumulative distribution function or the density function is intended.
It may be expedient to describe a population in terms of a few measures that summarize interesting features of the distribution. One such measure, computed from the population values, is called a parameter . Many different parameters can be defined to measure different aspects of a distribution.
The most commonly used parameter is the (arithmetic) mean . If the population contains a finite number of values, then the population mean is computed as the sum of all the values in the population divided by the number of elements in the population. For an infinite population, the concept of the mean is similar but requires more complicated mathematics.
E( x ) denotes the mean of a population of values symbolized by x , such as height, where E stands for expected value . You can also consider expected values of derived functions of the original values. For example, if x represents height, then E ( x 2 ) is the expected value of height squared, that is, the mean value of the population obtained by squaring every value in the population of heights.
Samples and Statistics
It is often impossible to measure all of the values in a population. A collection of measured values is called a sample . A mathematical function of a sample of values is called a statistic . A statistic is to a sample as a parameter is to a population. It is customary to denote statistics by Roman letters and parameters by Greek letters . For example, the population mean is often written as ¼ , whereas the sample mean is written as x . The field of statistics is largely concerned with the study of the behavior of sample statistics.
Samples can be selected in a variety of ways. Most SAS procedures assume that the data constitute a simple random sample , which means that the sample was selected in such a way that all possible samples were equally likely to be selected.
Statistics from a sample can be used to make inferences, or reasonable guesses, about the parameters of a population. For example, if you take a random sample of 30 students from the high school, then the mean height for those 30 students is a reasonable guess, or estimate , of the mean height of all the students in the high school. Other statistics, such as the standard error, can provide information about how good an estimate is likely to be.
For any population parameter, several statistics can estimate it. Often, however, there is one particular statistic that is customarily used to estimate a given parameter.
For example, the sample mean is the usual estimator of the population mean. In the case of the mean, the formulas for the parameter and the statistic are the same. In other cases, the formula for a parameter may be different from that of the most commonly used estimator. The most commonly used estimator is not necessarily the best estimator in all applications.
Measures of Location
Measures of location include the mean, the median, and the mode. These measures describe the center of a distribution. In the definitions that follow, notice that if the entire sample changes by adding a fixed amount to each observation, then these measures of location are shifted by the same fixed amount.
The Mean
The population mean ˆ’ = E( x ) is usually estimated by the sample mean x .
The Median
The population median is the central value, lying above and below half of the population values. The sample median is the middle value when the data are arranged in ascending or descending order. For an even number of observations, the midpoint between the two middle values is usually reported as the median.
The Mode
The mode is the value at which the density of the population is at a maximum. Some densities have more than one local maximum (peak) and are said to be multimodal . The sample mode is the value that occurs most often in the sample. By default, PROC UNIVARIATE reports the lowest such value if there is a tie for the most-often-occurring sample value. PROC UNIVARIATE lists all possible modes when you specify the MODES option in the PROC statement. If the population is continuous, then all sample values occur once, and the sample mode has little use.
Percentiles
Percentiles, including quantiles, quartiles, and the median, are useful for a detailed study of a distribution. For a set of measurements arranged in order of magnitude, the p th percentile is the value that has p percent of the measurements below it and (100 ˆ’ p ) percent above it. The median is the 50th percentile. Because it may not be possible to divide your data so that you get exactly the desired percentile, the UNIVARIATE procedure uses a more precise definition.
The upper quartile of a distribution is the value below which 75 percent of the measurements fall (the 75th percentile). Twenty-five percent of the measurements fall below the lower quartile value.
Quantiles
In the following example, SAS artificially generates the data with a pseudorandom number function. The UNIVARIATE procedure computes a variety of quantiles and measures of location, and outputs the values to a SAS data set. A DATA step then uses the SYMPUT routine to assign the values of the statistics to macro variables. The macro %FORMGEN uses these macro variables to produce value labels for the FORMAT procedure. PROC CHART uses the resulting format to display the values of the statistics on a histogram.
options nodate pageno=1 linesize=80 pagesize=52; title 'Example of Quantiles and Measures of Location'; data random; drop n; do n=1 to 1000; X=floor(exp(rannor(314159)*.8+1.8)); output; end; run; proc univariate data=random nextrobs=0; var x; output out=location mean=Mean mode=Mode median=Median q1=Q1 q3=Q3 p5=P5 p10=P10 p90=P90 p95=P95 max=Max; run; proc print data=location noobs; run; data _null_; set location; call symput('MEAN',round(mean,1)); call symput('MODE',mode); call symput('MEDIAN',round(median,1)); call symput('Q1',round(q1,1)); call symput('Q3',round(q3,1)); call symput('P5',round(p5,1)); call symput('P10',round(p10,1)); call symput('P90',round(p90,1)); call symput('P95',round(p95,1)); call symput('MAX',min(50,max)); run; %macro formgen; %do i=1 %to &max; %let value=&i; %if &i=&p5 %then %let value=&value P5; %if &i=&p10 %then %let value=&value P10; %if &i=&q1 %then %let value=&value Q1; %if &i=&mode %then %let value=&value Mode; %if &i=&median %then %let value=&value Median; %if &i=&mean %then %let value=&value Mean; %if &i=&q3 %then %let value=&value Q3; %if &i=&p90 %then %let value=&value P90; %if &i=&p95 %then %let value=&value P95; %if &i=&max %then %let value=>=&value; &i="&value" %end; %mend; proc format print; value stat %formgen; run; options pagesize=42 linesize=80; proc chart data=random; vbar x / midpoints=1 to &max by 1; format x stat.; footnote 'P5 = 5TH PERCENTILE'; footnote2 'P10 = 10TH PERCENTILE'; footnote3 'P90 = 90TH PERCENTILE'; footnote4 'P95 = 95TH PERCENTILE'; footnote5 'Q1 = 1ST QUARTILE '; footnote6 'Q3 = 3RD QUARTILE '; run; Example of Quantiles and Measures of Location 1 The UNIVARIATE Procedure Variable: X Moments N 1000 Sum Weights 1000 Mean 7.605 Sum Observations 7605 Std Deviation 7.38169794 Variance 54.4894645 Skewness 2.73038523 Kurtosis 11.1870588 Uncorrected SS 112271 Corrected SS 54434.975 Coeff Variation 97.0637467 Std Error Mean 0.23342978 Basic Statistical Measures Location Variability Mean 7.605000 Std Deviation 7.38170 Median 5.000000 Variance 54.48946 Mode 3.000000 Range 62.00000 Interquartile Range 6.00000 Tests for Location: Mu0=0 Test -Statistic- -----p Value------ Students t t 32.57939 Pr > t <.0001 Sign M 494.5 Pr >= M <.0001 Signed Rank S 244777.5 Pr >= S <.0001 Quantiles (Definition 5) Quantile Estimate 100% Max 62.0 99% 37.5 95% 21.5 90% 16.0 75% Q3 9.0 50% Median 5.0 25% Q1 3.0 10% 2.0 5% 1.0 1% 0.0 0% Min 0.0
Example of Quantiles and Measures of Location 2 Mean Max P95 P90 Q3 Median Q1 P10 P5 Mode 7.605 62 21.5 16 9 5 3 2 1 3
Example of Quantiles and Measures of Location 3 Frequency 120 + * * ** *** 90 +***** ***** ******* ******* 60 +******* ********* ********* ********* 30 +************ ************ * **************** * *********************** * * --------------------------------------------------- 1234567891111111111222222222233333333334444444444> 0123456789012345678901234567890123456789= 5 PPQ M MQ 0 511 e e3 P P 0 d a 9 9 i n 0 5 M a o n d e X Midpoint P5 = 5TH PERCENTILE P10 = 10TH PERCENTILE P90 = 90TH PERCENTILE P95 = 95TH PERCENTILE Q1 = 1ST QUARTILE Q3 = 3RD QUARTILE
Measures of Variability
Another group of statistics is important in studying the distribution of a population. These statistics measure the variability , also called the spread, of values. In the definitions given in the sections that follow, notice that if the entire sample is changed by the addition of a fixed amount to each observation, then the values of these statistics are unchanged. If each observation in the sample is multiplied by a constant, however, then the values of these statistics are appropriately rescaled.
The Range
The sample range is the difference between the largest and smallest values in the sample. For many populations, at least in statistical theory, the range is infinite, so the sample range may not tell you much about the population. The sample range tends to increase as the sample size increases . If all sample values are multiplied by a constant, then the sample range is multiplied by the same constant.
The Interquartile Range
The interquartile range is the difference between the upper and lower quartiles. If all sample values are multiplied by a constant, then the sample interquartile range is multiplied by the same constant.
The Variance
The population variance, usually denoted by ƒ 2 , is the expected value of the squared difference of the values from the population mean:
The sample variance is denoted by s 2 . The difference between a value and the mean is called a deviation from the mean . Thus, the variance approximates the mean of the squared deviations.
When all the values lie close to the mean, the variance is small but never less than zero. When values are more scattered , the variance is larger. If all sample values are multiplied by a constant, then the sample variance is multiplied by the square of the constant.
Sometimes values other than n __ 1 are used in the denominator. The VARDEF= option controls what divisor the procedure uses.
The Standard Deviation
The standard deviation is the square root of the variance, or root-mean-square deviation from the mean, in either a population or a sample. The usual symbols are for the population and s for a sample. The standard deviation is expressed in the same units as the observations, rather than in squared units. If all sample values are multiplied by a constant, then the sample standard deviation is multiplied by the same constant.
Coefficient of Variation
The coefficient of variation is a unitless measure of relative variability. It is defined as the ratio of the standard deviation to the mean expressed as a percentage. The coefficient of variation is meaningful only if the variable is measured on a ratio scale. If all sample values are multiplied by a constant, then the sample coefficient of variation remains unchanged.
Measures of Shape
Skewness
The variance is a measure of the overall size of the deviations from the mean. Since the formula for the variance squares the deviations, both positive and negative deviations contribute to the variance in the same way. In many distributions, positive deviations may tend to be larger in magnitude than negative deviations, or vice versa. Skewness is a measure of the tendency of the deviations to be larger in one direction than in the other. For example, the data in the last example are skewed to the right.
Population skewness is defined as
Because the deviations are cubed rather than squared, the signs of the deviations are maintained . Cubing the deviations also emphasizes the effects of large deviations. The formula includes a divisor of ƒ 3 to remove the effect of scale, so multiplying all values by a constant does not change the skewness. Skewness can thus be interpreted as a tendency for one tail of the population to be heavier than the other. Skewness can be positive or negative and is unbounded.
Kurtosis
The heaviness of the tails of a distribution affects the behavior of many statistics. Hence it is useful to have a measure of tail heaviness. One such measure is kurtosis . The population kurtosis is usually defined as
Note: Some statisticians omit the subtraction of 3.
Because the deviations are raised to the fourth power, positive and negative deviations make the same contribution, while large deviations are strongly emphasized . Because of the divisor ƒ 4 , multiplying each value by a constant has no effect on kurtosis.
Population kurtosis must lie between __2 and + ˆ , inclusive. If M 3 represents population skewness and M 4 represents population kurtosis, then
Statistical literature sometimes reports that kurtosis measures the peakedness of a density. However, heavy tails have much more influence on kurtosis than does the shape of the distribution near the mean (Kaplansky 1945; Ali 1974; Johnson, et al. 1980).
Sample skewness and kurtosis are rather unreliable estimators of the corresponding parameters in small samples. They are better estimators when your sample is very large. However, large values of skewness or kurtosis may merit attention even in small samples because such values indicate that statistical methods that are based on normality assumptions may be inappropriate.
The Normal Distribution
One especially important family of theoretical distributions is the normal or Gaussian distribution. A normal distribution is a smooth symmetric function often referred to as "bell-shaped." Its skewness and kurtosis are both zero. A normal distribution can be completely specified by only two parameters: the mean and the standard deviation. Approximately 68 percent of the values in a normal population are within one standard deviation of the population mean; approximately 95 percent of the values are within two standard deviations of the mean; and about 99.7 percent are within three standard deviations. Use of the term normal to describe this particular kind of distribution does not imply that other kinds of distributions are necessarily abnormal or pathological.
Many statistical methods are designed under the assumption that the population being sampled is normally distributed. Nevertheless, most real-life populations do not have normal distributions. Before using any statistical method based on normality assumptions, you should consult the statistical literature to find out how sensitive the method is to nonnormality and, if necessary, check your sample for evidence of nonnormality.
In the following example, SAS generates a sample from a normal distribution with a mean of 50 and a standard deviation of 10. The UNIVARIATE procedure performs tests for location and normality. Because the data are from a normal distribution, all p -values from the tests for normality are greater than 0.15. The CHART procedure displays a histogram of the observations. The shape of the histogram is a belllike, normal density.
options nodate pageno=1 linesize=80 pagesize=52; title '10000 Obs Sample from a Normal Distribution'; title2 'with Mean=50 and Standard Deviation=10'; data normaldat; drop n; do n=1 to 10000; X=10*rannor(53124)+50; output; end; run; proc univariate data=normaldat nextrobs=0 normal mu0=50 loccount; var x; run; proc format; picture msd 20='20 3*Std' (noedit) 30='30 2*Std' (noedit) 40='40 1*Std' (noedit) 50='50 Mean ' (noedit) 60='60 1*Std' (noedit) 70='70 2*Std' (noedit) 80='80 3*Std' (noedit) other=' '; run; options linesize=80 pagesize=42; proc chart; vbar x / midpoints=20 to 80 by 2; format x msd.; run;
10000 Obs Sample from a Normal Distribution 1 with Mean=50 and Standard Deviation=10 The UNIVARIATE Procedure Variable: X Moments N 10000 Sum Weights 10000 Mean 50.0323744 Sum Observations 500323.744 Std Deviation 9.92013874 Variance 98.4091525 Skewness -0.019929 Kurtosis -0.0163755 Uncorrected SS 26016378 Corrected SS 983993.116 Coeff Variation 19.8274395 Std Error Mean 0.09920139 Basic Statistical Measures Location Variability Mean 50.03237 Std Deviation 9.92014 Median 50.06492 Variance 98.40915 Mode . Range 76.51343 Interquartile Range 13.28179 Tests for Location: Mu0=50 Test -Statistic- -----p Value------ Student'st t 0.32635 Pr > t 0.7442 Sign M 26 Pr >= M 0.6101 Signed Rank S 174063 Pr >= S 0.5466 Location Counts: Mu0=50.00 Count Value Num Obs > Mu0 5026 Num Obs ^= Mu0 10000 Num Obs < Mu0 4974 Tests for Normality Test --Statistic--- -----p Value------ Kolmogorov-Smirnov D 0.006595 Pr > D >0.1500 Cramer-von Mises W-Sq 0.049963 Pr > W-Sq >0.2500 Anderson-Darling A-Sq 0.371151 Pr > A-Sq >0.2500
10000 Obs Sample from a Normal Distribution 2 with Mean=50 and Standard Deviation=10 The UNIVARIATE Procedure Variable: X Quantiles (Definition 5) Quantile Estimate 100% Max 90.2105 99% 72.6780 95% 66.2221 90% 62.6678 75% Q3 56.7280 50% Median 50.0649 25% Q1 43.4462 10% 37.1139 5% 33.5454 1% 26.9189 0% Min 13.6971
10000 Obs Sample from a Normal Distribution 3 with Mean=50 and Standard Deviation=10 Frequency * 800 + *** **** ****** ******* 600 + ******* ********** *********** *********** 400 + ************ ************* *************** ***************** 200 + ****************** ******************* ********************** *************************** -------------------------------- 2 3 4 5 6 7 8 0 0 0 0 0 0 0 3 2 1 M 1 2 3 * * * e * * * S S S a S S S t t t n t t t d d d d d d X Midpoint
Sampling Distribution of the Mean
If you repeatedly draw samples of size n from a population and compute the mean of each sample, then the sample means themselves have a distribution. Consider a new population consisting of the means of all the samples that could possibly be drawn from the original population. The distribution of this new population is called a sampling distribution .
It can be proven mathematically that if the original population has mean ¼ and standard deviation ƒ , then the sampling distribution of the mean also has mean ¼ , but its standard deviation is ƒ / ![]() . The standard deviation of the sampling distribution of the mean is called the standard error of the mean . The standard error of the mean provides an indication of the accuracy of a sample mean as an estimator of the population mean.
. The standard deviation of the sampling distribution of the mean is called the standard error of the mean . The standard error of the mean provides an indication of the accuracy of a sample mean as an estimator of the population mean.
If the original population has a normal distribution, then the sampling distribution of the mean is also normal. If the original distribution is not normal but does not have excessively long tails, then the sampling distribution of the mean can be approximated by a normal distribution for large sample sizes.
The following example consists of three separate programs that show how the sampling distribution of the mean can be approximated by a normal distribution as the sample size increases. The first DATA step uses the RANEXP function to create a sample of 1000 observations from an exponential distribution.The theoretical population mean is 1.00, while the sample mean is 1.01, to two decimal places. The population standard deviation is 1.00; the sample standard deviation is 1.04.
This is an example of a nonnormal distribution. The population skewness is 2.00, which is close to the sample skewness of 1.97. The population kurtosis is 6.00, but the sample kurtosis is only 4.80.
options nodate pageno=1 linesize=80 pagesize=42; title '1000 Observation Sample'; title2 'from an Exponential Distribution'; data expodat; drop n; do n=1 to 1000; X=ranexp(18746363); output; end; run; proc format; value axisfmt .05='0.05' .55='0.55' 1.05='1.05' 1.55='1.55' 2.05='2.05' 2.55='2.55' 3.05='3.05' 3.55='3.55' 4.05='4.05' 4.55='4.55' 5.05='5.05' 5.55='5.55' other=' '; run; proc chart data=expodat ; vbar x / axis=300 midpoints=0.05 to 5.55 by .1; format x axisfmt.; run; options pagesize=64; proc univariate data=expodat noextrobs=0 normal mu0=1; var x;
run; 1000 Observation Sample 1 from an Exponential Distribution Frequency 300 + 250 + 200 + 150 + 100 +* * *** * ***** ***** * 50 +******** *********** ************ * *************** ** * ************************* *** *** * * * --------------------------------------------------------- 0 0 1 1 2 2 3 3 4 4 5 5 . . . . . . . . . . . . 0 5 0 5 0 5 0 5 0 5 0 5 5 5 5 5 5 5 5 5 5 5 5 5 X Midpoint
1000 Observation Sample 2 from an Exponential Distribution The UNIVARIATE Procedure Variable: X Moments N 1000 Sum Weights 1000 Mean 1.01176214 Sum Observations 1011.76214 Std Deviation 1.04371187 Variance 1.08933447 Skewness 1.96963112 Kurtosis 4.80150594 Uncorrected SS 2111.90777 Corrected SS 1088.24514 Coeff Variation 103.15783 Std Error Mean 0.03300507 Basic Statistical Measures Location Variability Mean 1.011762 Std Deviation 1.04371 Median 0.689502 Variance 1.08933 Mode . Range 6.63851 Interquartile Range 1.06252
Tests for Location: Mu0=1 Test -Statistic- -----p Value------ Student'st t 0.356374 Pr > t 0.7216 Sign M -140 Pr >= M <.0001 Signed Rank S -50781 Pr >= S <.0001 Tests for Normality Test --Statistic--- -----p Value------ Shapiro-Wilk W 0.801498 Pr < W <0.0001 Kolmogorov-Smirnov D 0.166308 Pr > D <0.0100 Cramer-von Mises W-Sq 9.507975 Pr > W-Sq <0.0050 Anderson-Darling A-Sq 54.5478 Pr > A-Sq <0.0050 Quantiles (Definition 5) Quantile Estimate 100% Max 6.63906758 99% 5.04491651 95% 3.13482318 90% 2.37803632 75% Q3 1.35733401 50% Median 0.68950221 25% Q1 0.29481436 10% 0.10219011 5% 0.05192799 1% 0.01195590 0% Min 0.00055441
The next DATA step generates 1000 different samples from the same exponential distribution. Each sample contains ten observations. The MEANS procedure computes the mean of each sample. In the data set that is created by PROC MEANS, each observation represents the mean of a sample of ten observations from an exponential distribution. Thus, the data set is a sample from the sampling distribution of the mean for an exponential population.
PROC UNIVARIATE displays statistics for this sample of means. Notice that the mean of the sample of means is .99, almost the same as the mean of the original population. Theoretically, the standard deviation of the sampling distribution is ƒ / ![]() = 1.00/
= 1.00/ ![]() = 32, whereas the standard deviation of this sample from thesampling distribution is .30. The skewness (.55) and kurtosis (-.006) are closer to zero in the sample from the sampling distribution than in the original sample from the exponential distribution. This is so because the sampling distribution is closer to a normal distribution than is the original exponential distribution. The CHART procedure displays a histogram of the 1000-sample means. The shape of the histogram is much closer to a belllike, normal density, but it is still distinctly lopsided.
= 32, whereas the standard deviation of this sample from thesampling distribution is .30. The skewness (.55) and kurtosis (-.006) are closer to zero in the sample from the sampling distribution than in the original sample from the exponential distribution. This is so because the sampling distribution is closer to a normal distribution than is the original exponential distribution. The CHART procedure displays a histogram of the 1000-sample means. The shape of the histogram is much closer to a belllike, normal density, but it is still distinctly lopsided.
options nodate pageno=1 linesize=80 pagesize=48; title '1000 Sample Means with 10 Obs per Sample'; title2 'Drawn from an Exponential Distribution'; data samp10; drop n; do Sample=1 to 1000; do n=1 to 10; X=ranexp(433879); output; end; end; proc means data=samp10 noprint; output out=mean10 mean=Mean; var x; by sample; run; proc format; value axisfmt .05='0.05' .55='0.55' 1.05='1.05' 1.55='1.55' 2.05='2.05' other=' '; run; proc chart data=mean10; vbar mean/axis=300 midpoints=0.05 to 2.05 by .1; format mean axisfmt.; run; options pagesize=64; proc univariate data=mean10 noextrobs=0 normal mu0=1; var mean;
run; 1000 Sample Means with 10 Obs per Sample 1 Drawn from an Exponential Distribution Frequency 300 + 250 + 200 + 150 + * * * * * * * * * * * * 100+ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * 50+ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * -------------------------------------------- 0 0 1 1 2 . . . . . 0 5 0 5 0 5 5 5 5 5 Mean Midpoint
1000 Sample Means with 10 Obs per Sample 2 Drawn from an Exponential Distribution The UNIVARIATE Procedure Variable: Mean Moments N 1000 Sum Weights 1000 Mean 0.9906857 Sum Observations 990.685697 Std Deviation 0.30732649 Variance 0.09444957 Skewness 0.54575615 Kurtosis -0.0060892 Uncorrected SS 1075.81327 Corrected SS 94.3551193 Coeff Variation 31.0215931 Std Error Mean 0.00971852 Basic Statistical Measures Location Variability Mean 0.990686 Std Deviation 0.30733 Median 0.956152 Variance 0.09445 Mode . Range 1.79783 Interquartile Range 0.41703
Tests for Location: Mu0=1 Test -Statistic- -----p Value------ Student'st t -0.95841 Pr > t 0.3381 Sign M -53 Pr >= M 0.0009 Signed Rank S -22687 Pr >= S 0.0129 Tests for Normality Test --Statistic--- -----p Value------ Shapiro-Wilk W 0.9779 Pr < W <0.0001 Kolmogorov-Smirnov D 0.055498 Pr > D <0.0100 Cramer-von Mises W-Sq 0.953926 Pr > W-Sq <0.0050 Anderson-Darling A-Sq 5.945023 Pr > A-Sq <0.0050 Quantiles (Definition 5) Quantile Estimate 100% Max 2.053899 99% 1.827503 95% 1.557175 90% 1.416611 75% Q3 1.181006 50% Median 0.956152 25% Q1 0.763973 10% 0.621787 5% 0.553568 1% 0.433820 0% Min 0.256069
In the following DATA step, the size of each sample from the exponential distribution is increased to 50. The standard deviation of the sampling distribution is smaller than in the previous example because the size of each sample is larger. Also, the sampling distribution is even closer to a normal distribution, as can be seen from the histogram and the skewness.
options nodate pageno=1 linesize=80 pagesize=48; title '1000 Sample Means with 50 Obs per Sample'; title2 'Drawn from an Exponential Distribution'; data samp50; drop n; do sample=1 to 1000; do n=1 to 50; X=ranexp(72437213); output; end; end; proc means data=samp50 noprint; output out=mean50 mean=Mean; var x; by sample; run; proc format; value axisfmt .05='0.05' .55='0.55' 1.05='1.05' 1.55='1.55' 2.05='2.05' 2.55='2.55' other=' '; run; proc chart data=mean50; vbar mean / axis=300 midpoints=0.05 to 2.55 by .1; format mean axisfmt.; run; options pagesize=64; proc univariate data=mean50 nextrobs=0 normal mu0=1; var mean;
run; 1000 Sample Means with 50 Obs per Sample 1 Drawn from an Exponential Distribution Frequency 300 + * * * + * * * * * * * * * * + * * * * * * * * * * * * * 150+ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * 50+ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * ------------------------------------------------------ 0 0 1 1 2 2 . . . . . . 0 5 0 5 0 5 5 5 5 5 5 5 Mean Midpoint
1000 Sample Means with 50 Obs per Sample 2 Drawn from an Exponential Distribution The UNIVARIATE Procedure Variable: Mean Moments N 1000 Sum Weights 1000 Mean 0.99679697 Sum Observations 996.796973 Std Deviation 0.13815404 Variance 0.01908654 Skewness 0.19062633 Kurtosis -0.1438604 Uncorrected SS 1012.67166 Corrected SS 19.067451 Coeff Variation 13.8597969 Std Error Mean 0.00436881 Basic Statistical Measures Location Variability Mean 0.996797 Std Deviation 0.13815 Median 0.996023 Variance 0.01909 Mode . Range 0.87040 Interquartile Range 0.18956
Tests for Location: Mu0=1 Test -Statistic- -----p Value------ Student's t t -0.73316 Pr > t 0.4636 Sign M -13 Pr >= M 0.4292 Signed Rank S -10767 Pr >= S 0.2388 Tests for Normality Test --Statistic--- -----p Value------ Shapiro-Wilk W 0.996493 Pr < W 0.0247 Kolmogorov-Smirnov D 0.023687 Pr > D >0.1500 Cramer-von Mises W-Sq 0.084468 Pr > W-Sq 0.1882 Anderson-Darling A-Sq 0.66039 Pr > A-Sq 0.0877 Quantiles (Definition 5) Quantile Estimate 100% Max 1.454957 99% 1.337016 95% 1.231508 90% 1.179223 75% Q3 1.086515 50% Median 0.996023 25% Q1 0.896953 10% 0.814906 5% 0.780783 1% 0.706588 0% Min 0.584558
Testing Hypotheses
Defining a Hypothesis
The purpose of the statistical methods that have been discussed so far is to estimate a population parameter by means of a sample statistic. Another class of statistical methods is used for testing hypotheses about population parameters or for measuring the amount of evidence against a hypothesis.
Consider the universe of students in a college. Let the variable X be the number of pounds by which a students weight deviates from the ideal weight for a person of the same sex, height, and build. You want to find out whether the population of students is, on the average, underweight or overweight. To this end, you have taken a random sample of X values from nine students, with results as given in the following DATA step:
title 'Deviations from Normal Weight'; data x; input X @@; datalines; -7 -2 1 3 6 10 15 21 30 ;
You can define several hypotheses of interest. One hypothesis is that, on the average, the students are of exactly ideal weight. If represents the population mean of the X values, then you can write this hypothesis, called the null hypothesis, as .
The other two hypotheses, called alternative hypotheses, are that the students are underweight on the average, H 1 : ¼ < 0, and that the students are overweight on the average, H 2 : ¼ > 0.
The null hypothesis is so called because in many situations it corresponds to the assumption of no effect or no difference. However, this interpretation is not appropriate for all testing problems. The null hypothesis is like a straw man that can be toppled by statistical evidence. You decide between the alternative hypotheses according to which way the straw man falls .
A naive way to approach this problem would be to look at the sample mean ![]() and decide among the three hypotheses according to the following rule:
and decide among the three hypotheses according to the following rule:
-
If iconid=px, then decide on H 1 : ¼ < 0
-
If iconid=px, then decide on H 2 : ¼ = 0
-
If iconid=px, then decide on H 3 : ¼ > 0
The trouble with this approach is that there may be a high probability of making an incorrect decision. If H is true, then you are nearly certain to make a wrong decision because the chances of ![]() being exactly zero are almost nil. If ¼ is slightly less than zero, so that H 1 is true, then there may be nearly a 50 percent chance that
being exactly zero are almost nil. If ¼ is slightly less than zero, so that H 1 is true, then there may be nearly a 50 percent chance that ![]() will be greater than zero in repeated sampling, so the chances of incorrectly choosing H 2 would also be nearly 50 percent. Thus, you have a high probability of making an error if
will be greater than zero in repeated sampling, so the chances of incorrectly choosing H 2 would also be nearly 50 percent. Thus, you have a high probability of making an error if ![]() is near zero. In such cases, there is not enough evidence to make a confident decision, so the best response may be to reserve judgment until you can obtain more evidence.
is near zero. In such cases, there is not enough evidence to make a confident decision, so the best response may be to reserve judgment until you can obtain more evidence.
The question is, how far from zero must ![]() be for you to be able to make a confident decision? The answer can be obtained by considering the sampling distribution of
be for you to be able to make a confident decision? The answer can be obtained by considering the sampling distribution of ![]() . If X has a roughly normal distribution, then
. If X has a roughly normal distribution, then ![]() has an approximately normal sampling distribution. The mean of the sampling distribution of
has an approximately normal sampling distribution. The mean of the sampling distribution of ![]() is ¼ . Assume temporarily that ƒ , the standard deviation of X, is known to be 12. Then the standard error of for samples of nine observations is
is ¼ . Assume temporarily that ƒ , the standard deviation of X, is known to be 12. Then the standard error of for samples of nine observations is ![]() .
.
You know that about 95 percent of the values from a normal distribution are within two standard deviations of the mean, so about 95 percent of the possible samples of nine X values have a sample mean iconid=px between 0 ˆ’ 2 (4) and 0 + 2 (4), or between ˆ’ 8 and 8. Consider the chances of making an error with the following decision rule:
-
If
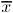 , then decide on H 1 : ¼ < 0.
, then decide on H 1 : ¼ < 0. -
If ˆ’ 8
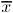 8, then reserve judgment.
8, then reserve judgment. -
If
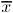 > 8, then decide on H 2 : ¼ > 0 .
> 8, then decide on H 2 : ¼ > 0 .
If H is true, then in about 95 percent of the possible samples ![]() will be between the critical values ˆ’ 8 and 8, so you will reserve judgment. In these cases the statistical evidence is not strong enough to fell the straw man. In the other 5 percent of the samples you will make an error; in 2.5 percent of the samples you will incorrectly choose H 1 , and in 2.5 percent you will incorrectly choose H 2 .
will be between the critical values ˆ’ 8 and 8, so you will reserve judgment. In these cases the statistical evidence is not strong enough to fell the straw man. In the other 5 percent of the samples you will make an error; in 2.5 percent of the samples you will incorrectly choose H 1 , and in 2.5 percent you will incorrectly choose H 2 .
The price you pay for controlling the chances of making an error is the necessity of reserving judgment when there is not sufficient statistical evidence to reject the null hypothesis.
Significance and Power
The probability of rejecting the null hypothesis if it is true is called the Type I error rate of the statistical test and is typically denoted as . In this example, an ![]() value less than ˆ’ 8 or greater than 8 is said to be statistically significant at the 5 percent level. You can adjust the type I error rate according to your needs by choosing different critical values. For example, critical values of ˆ’ 4 and 4 would produce a significance level of about 32 percent, while ˆ’ 12 and 12 would give a type I error rate of about 0.3 percent.
value less than ˆ’ 8 or greater than 8 is said to be statistically significant at the 5 percent level. You can adjust the type I error rate according to your needs by choosing different critical values. For example, critical values of ˆ’ 4 and 4 would produce a significance level of about 32 percent, while ˆ’ 12 and 12 would give a type I error rate of about 0.3 percent.
The decision rule is a two-tailed test because the alternative hypotheses allow for population means either smaller or larger than the value specified in the null hypothesis. If you were interested only in the possibility of the students being overweight on the average, then you could use a one-tailed test :
-
If
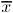 8, then reserve judgment.
8, then reserve judgment. -
If
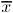 > 8, then decide on H 2 ¼ > 0 .
> 8, then decide on H 2 ¼ > 0 .
For this one-tailed test, the type I error rate is 2.5 percent, half that of the two-tailed test.
The probability of rejecting the null hypothesis if it is false is called the power of the statistical test and is typically denoted as 1 ˆ’ ² . ² is called the Type II error rate , which is the probability of not rejecting a false null hypothesis. The power depends on the true value of the parameter. In the example, assume the population mean is 4. The power for detecting H 2 is the probability of getting a sample mean greater than 8. The critical value 8 is one standard error higher than the population mean 4. The chance of getting a value at least one standard deviation greater than the mean from a normal distribution is about 16 percent, so the power for detecting the alternative hypothesis H 2 is about 16 percent. If the population mean were 8, then the power for H 2 would be 50 percent, whereas a population mean of 12 would yield a power of about 84 percent.
The smaller the type I error rate is, the less the chance of making an incorrect decision, but the higher the chance of having to reserve judgment. In choosing a type I error rate, you should consider the resulting power for various alternatives of interest.
Students t Distribution
In practice, you usually cannot use any decision rule that uses a critical value based on because you do not usually know the value of ƒ . You can, however, use s as an estimate of ƒ . Consider the following t statistic:
This t statistic is the difference between the sample mean and the hypothesized mean ¼ divided by the estimated standard error of the mean.
If the null hypothesis is true and the population is normally distributed, then the t statistic has what is called a Students t distribution with n ˆ’ 1 degrees of freedom. This distribution looks very similar to a normal distribution, but the tails of the Students t distribution are heavier. As the sample size gets larger, the sample standard deviation becomes a better estimator of the population standard deviation, and the t distribution gets closer to a normal distribution.
You can base a decision rule on the t statistic:
-
If t < ˆ’ 2.3, then decide on H 1 : ¼ < 0.
-
If ˆ’ 2.3 t 2.3, then reserve judgment.
-
If t > 2.3, then decide on H : ¼ > 0.
The value 2.3 was obtained from a table of Students t distribution to give a type I error rate of 5 percent for 8 (that is, 9 ˆ’ 1 = 8) degrees of freedom. Most common statistics texts contain a table of Students t distribution. If you do not have a statistics text handy, then you can use the DATA step and the TINV function to print any values from the t distribution.
By default, PROC UNIVARIATE computes a t statistic for the null hypothesis that ¼ = 0, along with related statistics. Use the MU0= option in the PROC statement to specify another value for the null hypothesis.
This example uses the data on deviations from normal weight, which consist of nine observations. First, PROC MEANS computes the t statistic for the null hypothesis that ¼ = 0. Then, the TINV function in a DATA step computes the value of Students t distribution for a two-tailed test at the 5 percent level of significance and 8 degrees of freedom.
data devnorm; title 'Deviations from Normal Weight'; input X @@; datalines; -7 -2 1 3 6 10 15 21 30 ; proc means data=devnorm maxdec=3 n mean std stderr t probt; run; title 'Student''s t Critical Value'; data _null_; file print; t=tinv(.975,8); put t 5.3; run;
Deviations from Normal Weight 1 The MEANS Procedure Analysis Variable : X N Mean Std Dev Std Error t Value Pr > t -------------------------------------------------------------- 9 8.556 11.759 3.920 2.18 0.0606 --------------------------------------------------------------
Student's t Critical Value 2 2.306
In the current example, the value of the t statistic is 2.18, which is less than the critical t value of 2.3 (for a 5 percent significance level and 8 degrees of freedom). Thus, at a 5 percent significance level you must reserve judgment. If you had elected to use a 10 percent significance level, then the critical value of the t distribution would have been 1.86 and you could have rejected the null hypothesis. The sample size is so small, however, that the validity of your conclusion depends strongly on how close the distribution of the population is to a normal distribution.
Probability Values
Another way to report the results of a statistical test is to compute a probability value or p-value . A p -value gives the probability in repeated sampling of obtaining a statistic as far in the direction(s) specified by the alternative hypothesis as is the value actually observed . A two-tailed p -value for a t statistic is the probability of obtaining an absolute t value that is greater than the observed absolute t value. A one-tailed p -value for a t statistic for the alternative hypothesis ¼ > ¼ is the probability of obtaining a t value greater than the observed t value. Once the p -value is computed, you can perform a hypothesis test by comparing the p -value with the desired significance level. If the p -value is less than or equal to the type I error rate of the test, then the null hypothesis can be rejected. The two-tailed p -value, labeled Pr > t in the PROC MEANS output, is .0606, so the null hypothesis could be rejected at the 10 percent significance level but not at the 5 percent level.
A p -value is a measure of the strength of the evidence against the null hypothesis. The smaller the p -value, the stronger the evidence for rejecting the null hypothesis.
Note: For a more thorough discussion, consult an introductory statistics textbook such as Mendenhall and Beaver (1998); Ott and Mendenhall (1994); or Snedecor and Cochran (1989).
EAN: 2147483647
Pages: 260
- Telecommunications and Network Security
- Business Continuity Planning and Disaster Recovery Planning
- The Accreditation Phase
- Appendix C The Information System Security Architecture Professional (ISSAP) Certification
- Appendix D The Information System Security Engineering Professional (ISSEP) Certification