Section 3.4. Small-Scale Channel Modeling
|
3.4. Small-Scale Channel ModelingIn the previous section we concentrated on what is termed statistical modeling of the large-scale characteristics of the received signal. This is primarily concerned with the loss in received signal power versus distance (and possibly frequency) between the transmitter and receiver. It was noted that even when modeling relatively simple signal parameters, UWB presents some interesting challenges, and care must be taken when applying a model to a UWB system. We now turn to a more complex part of channel modeling, the statistical modeling of the small-scale characteristics. The small-scale characteristics include the small-scale fading in a local environment as well as the distortion of the transmitted waveform due to multipath. UWB signals are often proposed for short-range applications (d <10m). As a result, when discussing fading (that is, the loss in received signal power) there is some ambiguity in the definition of large-scale and small-scale. In this text when we discuss signal fading we will typically restrict the term "small-scale" to refer to fading within a 1 m2 area. Large-scale fading will refer to fading over distances much greater than 1 m. Again, in this section we are concerned with statistical modeling of the received signal characteristics. While the statistical properties of the large-scale characteristics are necessary for proper link budget design, the statistical properties of the small-scale characteristics are needed for proper receiver design. Specifically, understanding small-scale fading and signal correlation over a small area aids in the evaluation of the receiver, diversity mechanisms, and potential multiple antenna applications. Additionally, understanding the waveform distortion suffered by a UWB signal is vital in designing the modulation scheme and the signal demodulator, as well as for evaluating receiver structures. The received signal from a UWB transmission can be represented as shown in Chapter 4. Specifically, in (4.44) the received signal is given as Equation 3.41 where Equation 3.42 where the vector nature of the responses is now incorporated into the scalar time domain impulse response of the channel, and ht A direct unobstructed LOS path with no reflectors/diffractors in the environment is very nearly equivalent to free-space. Therefore, if a received pulse from only the LOS path can be isolated from pulses arriving along other paths through time gating, this pulse can be used to determine the channel impulse response. These combined effects can then be removed from the received signal by deconvolving the LOS pulse from the received signal to estimate the channel impulse response where Equation 3.43 It must be noted that the angular dependencies of the antennas, and thus the vector nature of the problem, are subsumed into the channel response. Therefore, the channel impulse response that is calculated is not strictly only due to the channel. The measured channel impulse response for directional antennas, such as TEM horns, would not be influenced significantly by reflectors/diffractors behind the antennas. However, the channel impulse response for omni-directional, in one plane only, antennas would be affected more by reflectors/diffractors in the environment than by directional antennas. Additionally, by only considering the antenna response at the boresite we are assuming that the pulse distortion due to the antenna is the same from all transmit/receive directions. While this is clearly a big assumption, it is justified by the fact that the strongest paths will be those transmitted and received via the boresite. Broadly speaking, all omni-directional antennas will behave in a similar fashion. The same could be said of directional antennas, with the same approximate gain. Thus, the characterizations of the "channel" for antennas such as TEM horns and bicones should be performed separately but may be representative of many antenna structures. Channel modeling thus depends on how the channel parameters are obtained from the measurements, that is, on deconvolution. Deconvolution is the process of separating two signals that have been combined by convolution. Several deconvolution techniques have been developed [52], often for specific types of signals or for use with a specific application. Deconvolution can be performed in the time domain or the frequency domain. Different techniques will emphasize different aspects of the deconvolved signal and can offer different advantages depending on the further analysis desired. In the frequency domain, the most straightforward deconvolution method is known as inverse filtering [53]. Another technique that has been widely used is the Van-Cittert deconvolution technique. This iterative method can be performed in either the time or frequency domain. Reference [54] proposes using this technique in the frequency domain and also proposes criteria to optimize the necessary number of iterations. Regardless of which frequency domain technique is used, such a process results in a bandlimited impulse response. The impact of this will be discussed shortly. A third deconvolution technique often considered is the CLEAN algorithm, which is a time domain technique. The CLEAN algorithm was first introduced in [33] and has been used by many researchers in UWB channel measurement analysis [41,55,72]. The algorithm is important in channel modeling because it assumes that the impulse response being found is not bandlimited but is rather a sum of scaled and time-delayed impulses. This is consistent with classic small-scale channel models and thus makes the CLEAN algorithm very useful. We will discuss the algorithm in more detail in Section 3.6.1. Examples of impulse responses generated by each deconvolution method for a specific measurement set are shown in Figure 3.11 for comparison [41]. The inverse filtering impulse response and the Van-Cittert impulse response are nearly identical, and the CLEAN impulse response shows the same primary features of the channel. Estimates of the received signal can be generated by convolving the impulse response with the LOS pulse used in the deconvolution. The measured signal is plotted with the estimates of this signal using the impulse responses from each of the three deconvolution techniques in Figure 3.12 [41]. Visually, the measured signal, the inverse filter reproduced signal, and the Van-Cittert reproduced signal are nearly identical. Noticeable differences are seen between the measured signal and the CLEAN reproduced signal, but the signals still agree reasonably well. Figure 3.11. Comparison of Example Impulse Responses Generated by the CLEAN Algorithm, Inverse Filtering, and the Van-Cittert Techniques with Bennia-Riad Criteria. (Note: The Latter Two Responses have been Scaled by 10 to Allow for Easier Visual Comparison.)SOURCE: D. McKinstry, "Ultra-Wideband Small-Scale Channel Modeling and its Application to Receiver Design" [41]. © D. McKinstry, 2002. Used by permission. 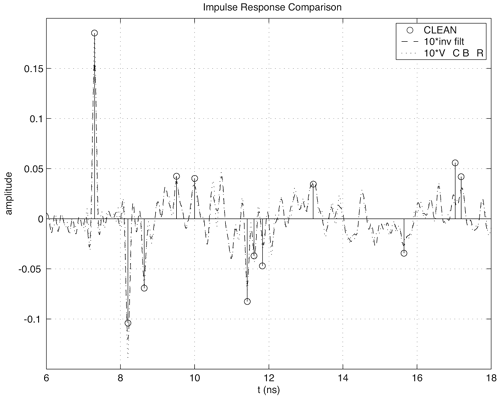 Figure 3.12. Comparison of Measured Signal with Estimates of the Received Signal Based on the Impulse Responses Generated by the CLEAN Algorithm, Inverse Filtering, and the Van-Cittert Techniques with Bennia-Riad Criteria.SOURCE: D. McKinstry, "Ultra-Wideband Small-Scale Channel Modeling and its Application to Receiver Design" [41]. © D. McKinstry, 2002. Used by permission. 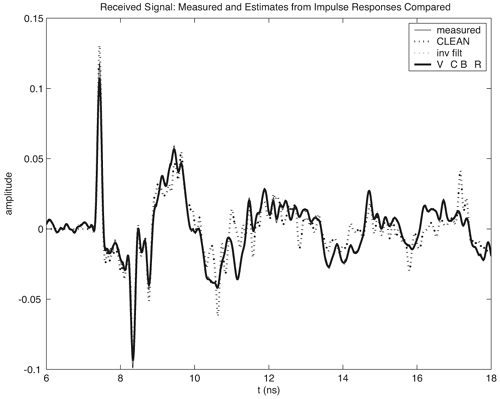 3.4.1. Statistical Modeling of the Channel Impulse ResponseAs discussed previously, the small-scale effects of the wireless channel are commonly described by a simple scalar impulse response as shown in (3.43). More specifically, the small-scale channel is typically modeled as a time-varying linear filter where the received signal is given by [26] Equation 3.44 where s(t) is the transmitted signal that is assumed to be the received LOS pulse in the case of UWB, h(t, t) is the time-varying channel impulse response, and n(t) is additive white Gaussian noise. The impulse response can change as a function of time (or as a function of spatial variation) due to the motion of the transmitter or receiver and/or changes in the channel itself. The channel is typically modeled using a tap-delay line approach [26, 38]. This approach was first proposed in [38], and well-established for indoor channels in [44,45]. Thus, the channel model can be given as Equation 3.45 where bk(t), tk(t), and pk(t) are the time-varying amplitude, delay, and polarity of the kth path respectively. N (t) is the number of multipath components, which is also in general a function of time. Note that for narrowband (or wideband) channels, the polarity, pk, is typically subsumed into a phase term, ejq(t) due to the use of the complex baseband. In UWB modeling researchers often ignore phase since it is assumed that baseband pulses are being sent. If the pulses are upconverted or downconverted, a complex baseband model may be appropriate, and the phase term could be reintroduced. If the channel is assumed to be static over the interval of interest, the time-invariant model of the channel can be used Equation 3.46 The main goal of small-scale channel models is to statistically characterize the amplitudes, delays, and polarities of the multipath components of the channel. We will discuss the standard models shortly. Besides specific statistical characterization of the multipath parameters, the channel can also be characterized by coarse statistics, such as mean excess delay, RMS delay spread, and maximum excess delay, that describe the time dispersive properties of the channel. These are useful as single number descriptions of the channel to estimate the performance and potential for intersymbol interference (ISI). These values tend to increase with greater transmitter/receiver separation [77]. The mean excess delay is defined as [26] Equation 3.47 The RMS delay spread of the channel is defined as Equation 3.48 The number of paths is the number of significant multipath components that form the channel and is also used as a shorthand way of characterizing the time dispersion of the channel. The key to any model that assumes the discrete channel presented previously is the joint statistical characterization of the path amplitudes and delays. Various wireless channel models for doing this are discussed next. The models were originally developed to characterize indoor wideband channels. Researchers have found that the general approaches are also useful for UWB channels. 3.4.2. Saleh-Valenzuela ModelThe most common statistical model for the discrete indoor channel impulse response is the Saleh-Valenzuela model [39]. It should be noted that although the Saleh-Valenzuela model was developed for NLOS channels, it has also been applied to LOS channels where it is perhaps less valid, unless LOS components are specifically added [14]. The Saleh-Valenzuela model is a tapped-delay line model given by Equation 3.49 where L is the number of paths per cluster and K is the number of clusters. The basic assumption behind this model is that the multipath components arrive in clusters. The cluster arrivals are described by a Poisson process, and thus, the cluster interarrival times Tl are described by exponential random variables Equation 3.50 where L is the mean cluster arrival rate. Within a cluster, the path arrivals are also described by a Poisson process, so that the distribution of the interarrival times is described as where l is the mean ray arrival rate. The average power of both the clusters and the rays within the clusters is assumed to decay exponentially such that the average power of a multipath component at a given delay, Tl + tk,l, is given by Equation 3.51 where The amplitude of each path is assumed to be a random variable about an exponential mean. Several distributions have been proposed for the amplitudes, although the original model assumed a Rayleigh distribution. The polarity is assumed to be a binary random variable with equal probability. When a random phase is used, the phase is assumed to be uniformly distributed. The Rayleigh distributed amplitudes and random phase model come from the assumption that several paths arrive at delays that are not resolvable to the measurement system used. This is a more valid assumption for wideband channels but is questionable for UWB channels. As a result, many researchers have found that log-normal or Nakagami distributions provide a better fit [71]. This will be discussed in more detail in Section 3.4.9. The use of log-normal random variables is especially convenient when they are also used for the cluster amplitudes. This suggests two independent log-normal variables to represent the amplitude variations of the clusters and rays. However, these random variables can be combined as a single log-normal random variable. The polarity of the path is represented as an equi-probable binary random variable, pk,l, taking on the values ±1. For log-normal amplitudes, the path amplitudes are given by Equation 3.52 where Equation 3.53 and Equation 3.54 To summarize, this model is described by five parameters:
An example CIR for the Saleh-Valenzuela model is given in Figure 3.13. Figure 3.13. Sample Saleh-Valenzuela Model CIR.SOURCE: S. Venkatesh, J. Ibrahim, and R. M. Buehrer, "A New 2-Cluster Model for Indoor UWB Channel Measurements," IEEE International Symposium on Antennas and Propagation [75]. © IEEE, 2004. Used by permission. 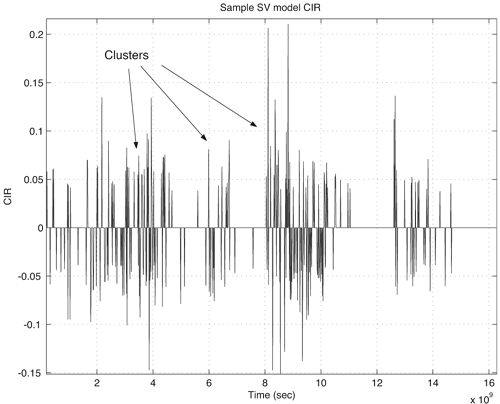 3.4.3. D-K ModelThe D-K model has also been used to model indoor wideband channels, and like the Saleh-Valenzuela model is based on the assumption that multipath components arrive in clusters. The probability that a path arrives at any given delay is higher by a factor of K if a path has arrived within the past D seconds. By increasing the arrival rate when a path has recently arrived, the paths tend to arrive in clusters. The arrival times thus follow a modified, two-state Poisson process, and the inter-arrival times follow an exponential distribution where the arrival rate is based on the state. When in state S-1, the mean arrival rate is given by l. The transition to state S-2 is triggered when a path occurs. In S-2 the mean arrival rate is given by Kl. If after D seconds a path has not arrived, transition back to S-1 occurs. Exponential energy decay is assumed here to describe the expected value of the energy in a path at a given delay. The polarity is assumed to be ±1 with equal likelihood, and amplitude fading is assumed to be log-normal such that the amplitude of a path is given by (3.52)-(3.54). For computer simulation, this model is often implemented using a discrete form. In the discrete version, the time axis is divided into bins, and the probability of a path arriving in a given bin is based on whether a path arrived in the previous bin (the probability being higher by a factor of K if a path was present). 3.4.4. Single Poisson ModelThis is a simplified version of both of the previously introduced models and assumes that only one cluster is present in the impulse response (or equivalently, no clustering of paths). The arrivals of paths are treated as a Poisson process with an arrival rate of l. Also, the decay of the paths is assumed to be exponential, with a decay time constant of g. The amplitudes of the paths are modeled as a log-normal random variable with parameter s. 3.4.5. Modified Poisson ModelA modified version of the single Poisson arrival time model with dominant early multipath components was developed to more accurately represent LOS channels [41]. The model is based on the characteristics observed in the measurement data. The first multipath components have significantly more energy than the later arriving components. The number of dominant components, M, is randomly chosen to be two, three, or four with equal likelihood. This agrees with the trends seen in some measurements. The interarrival times of the dominant components are exponentially distributed and given by Equation 3.55 where l1 is the mean arrival rate of the dominant components. The amplitude of each dominant component is given by a log-normal random variable with unit mean energy and fading parameter s1. The first component arrives at zero delay (t0 = 0) and has a positive polarity (p0 = +1) because this is assumed to be the LOS component, which will not be inverted. All other paths have an equi-probable positive or negative polarity. The interarrival times of the weaker components also follow an exponential interarrival, but with a different mean arrival rate l2. Equation 3.56 The mean energies of the weaker components follow a traditional exponential decay. The first component from this group has mean energy W dB less than the mean of the dominant components, and the respective means of the later components are taken relative to this first weak path. The weak path amplitudes are also log-normal variables with a different fading parameter, s2, such that Equation 3.57 3.4.6. Split-Poisson ModelThe Saleh-Valenzuela model is based on the generation of multiple exponentially decaying clusters. However, much measurement data indicates that very few clusters may exist, perhaps due to the limited range used for UWB systems and measurements. An example taken from [72] is shown in Figure 3.14. The data seems to indicate that the average CIR consists basically of two clusters, the first short cluster containing several strong paths that decay quickly and the longer second cluster containing slowly decaying paths. Based on the previous observation, the Split-Poisson model was proposed in [72, 75, 76]. This model assumes two clusters of Poisson arrivals, one delayed by t1 relative to the other. The first cluster is generated using a set of parameters l1, s1, g1 while the second cluster is generated using a separate set of parameters l2, s2, g1. The overall CIR is created by adding a delayed version of the second cluster to the first cluster. Also, in order to maintain continuity in the decay of energy in the overall CIR the first cluster is weighted higher than the second cluster by a factor a. This is shown in Figure 3.15. Each of these parameters is estimated from the data as described in [75, 76]. Figure 3.14. Average CIR Amplitude Over One Location From Example MeasurementTwo Clusters Can Be Clearly Seen.SOURCE: S. Venkatesh, J. Ibrahim, and R. M. Buehrer, "A New 2-Cluster Model for Indoor UWB Channel Measurements," IEEE International Symposium on Antennas and Propagation [75]. © IEEE, 2004. Used by permission. Figure 3.15. Illustration of the Two Cluster Model.SOURCE: S. Venkatesh, J. Ibrahim, and R. M. Buehrer, "A New 2-Cluster Model for Indoor UWB Channel Measurements," IEEE International Symposium on Antennas and Propagation [75]. © IEEE, 2004. Used by permission. 3.4.7. Effect of Model ParametersWe now illustrate how different model parameters affect the RMS delay spread and mean excess delay of the generated channel impulse response. For simplicity we consider the single Poisson model and begin with the parameters shown in Table 3.9. To examine the parameter impact we consider the measured cumulative histogram of the RMS delay spread, mean excess delay, and number of multipath components when the parameters l, g, and s, are (respectively) doubled, keeping the rest of the parameters fixed. Note that only paths within 20 dB of the strongest path are considered. Figures 3.16, 3.17, and 3.18 show the effect of doubling these parameters individually. We observe the following trends:
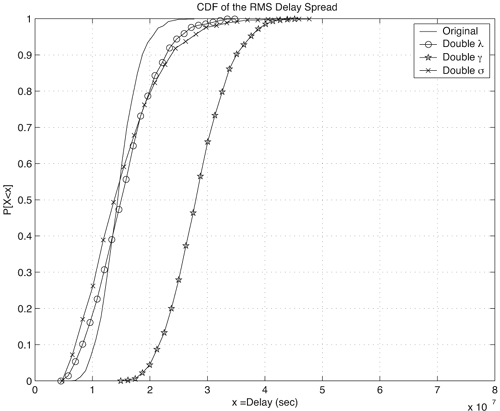
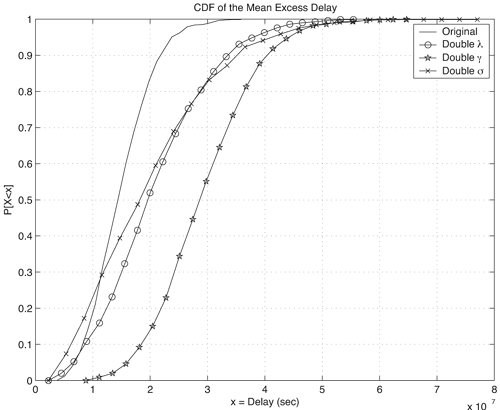
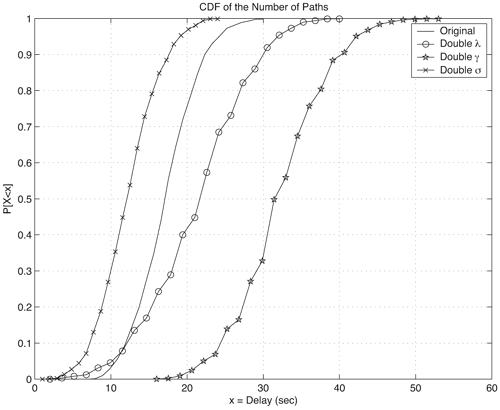
We can also examine the impact that the parameters of the Saleh-Valenzuela model have on the same statistics. For the Saleh-Valenzuela model, the parameters that may be varied are {l, L, g, G, s}. Figures 3.19, 3.20, and 3.21 show the effect of doubling the parameters {g, G, s} individually from the "original" parameters given in Table 3.10. We observe the following trends:
Figure 3.19. Effect of Doubling Saleh-Valenzuela Parameters {g, G, s} on CIR RMS Delay Spread.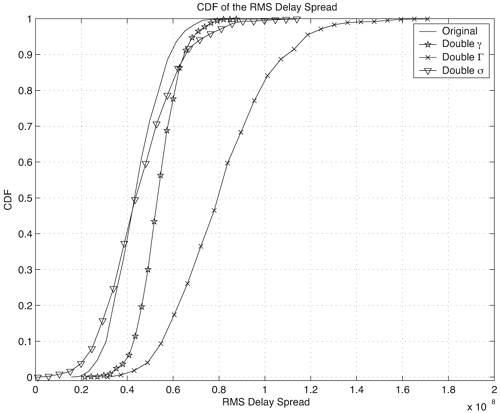 Figure 3.20. Effect of Doubling Saleh-Valenzuela Parameters {g, G, s} on CIR Mean Excess Delay.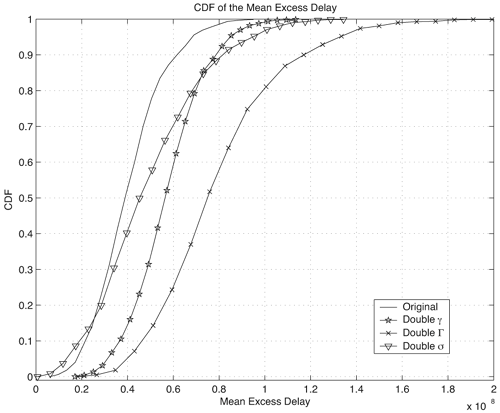 Figure 3.21. Effect of Doubling Saleh-Valenzuela Parameters {g, G, s} on CIR Number of Paths.
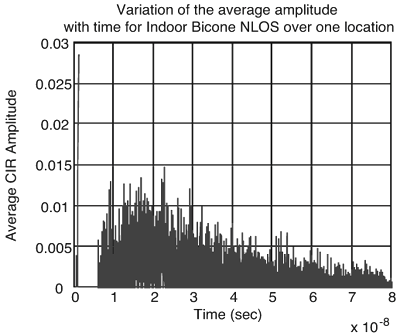
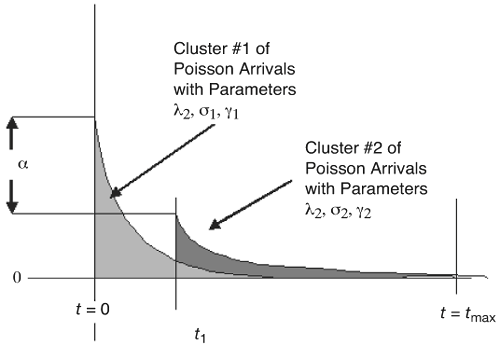
Figures 3.22, 3.23, and 3.24 show the effect of doubling the parameters {l, L} individually from the original parameters shown in Table 3.10. We observe the following trends:
Figure 3.22. Effect of Doubling Saleh-Valenzuela Parameters {l, L} on CIR EMS Delay Spread.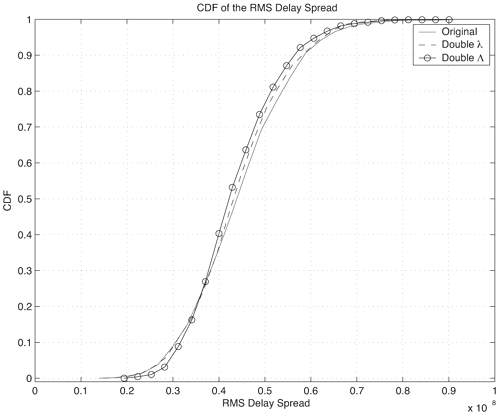 Figure 3.23. Effect of Doubling Saleh-Valenzuela Parameters {l, L} on CIR Mean Excess Delay.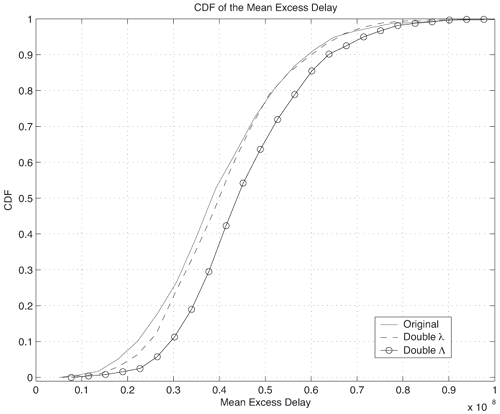 Figure 3.24. Effect of Doubling Saleh-Valenzuela Parameters {g, G, s} on CIR Number of Paths.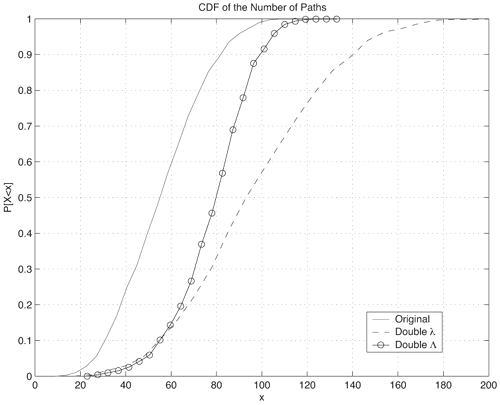 3.4.8. Stochastic Tapped-Delay Line ModelA similar model that has been proposed in the literature is termed a stochastic tapped-delay line (STDL) model [10]. Specifically, the approach is derived from measurements in an indoor environment and assumes that the average energy follows a single exponential decay. The power delay profile is written as Equation 3.61 The variable r is the power ratio of the second path to the first and is random following a log-normal distribution. The decay constant e is also modeled as a log-normal random variable. The previous expression provides the average power gains for each delay. The specific gain value is selected from a Gamma distribution with a mean energy that follows the exponential distribution given previously and an m value that is selected from a truncated Gaussian distribution. The model was used to compare total signal energy with measurements in [10], and good agreement was found. 3.4.9. Amplitude StatisticsIt is important to estimate the distribution of the path amplitudes while fitting the empirical data to a specific channel model. For example, the original Saleh-Valenzuela model assumed that the path amplitudes follow a Rayleigh distribution. This is due to the fact that a large number of multipath components combined in each resolvable path, resulting in a complex Gaussian random variable. However for the case of UWB baseband pulses, this cannot necessarily be assumed. The following path amplitudes can be defined from two different perspectives: global[4] amplitude distributions at different excess delays can be examined and local[5] amplitude distributions at different excess delays can be examined. Note that the amplitude distribution describes the variation of the received amplitude from the average delay profile. As mentioned earlier, the average power delay profile is commonly modeled as an exponential decay. Four probability distributions have been discussed in the literature to represent these local variations: (1) the log-normal distribution, (2) the Weibull distribution, (3) the Nakagami distribution, and (4) the Rayleigh distribution.
Log-normal variables are convenient because large-scale fading is also modeled as log-normal. The log-normal cumulative distribution function (CDF) can be written as Equation 3.62 This is equivalent to the normal distribution when the amplitudes are expressed in a log scale 20 log 10 (A). The received signal amplitudes are expressed in dB and the mean and the standard deviation is calculated using dB values. In [7], a Weibull distribution was found to represent the data best. The Weibull CDF is given as Equation 3.63 The Weibull parameters a and b are known as the normalization factor and the shape factor, respectively. The Weibull distribution simplifies to the Rayleigh distribution when b = 1. The amplitudes in this case are linear and not expressed in dB. The Weibull distribution is also sometimes used to fit the variation of the power of the channel impulse response about a decaying exponential mean [8]. The Rayleigh CDF is common for narrowband systems and is also used to model late arriving path amplitudes in UWB models. This represents the observed phenomenon that later arriving paths are more numerous, causing more fading. The Rayleigh CDF is given as Equation 3.64 where b Equation 3.65 where Equation 3.66 and Equation 3.67 where K is the Rice factor of the Rician distribution. As an example, consider Figure 3.25, which plots data taken from [72]. Global amplitude statistics are plotted for various delays for an indoor office environment. The measured cumulative histograms are compared with three distributions. In this example, the data is found to match a log-normal distribution. Figure 3.25. Global Amplitude Statistics Matched to Three Different Distributions at Different Excess Delays for the Gaussian Pulse. (It is Seen that the Log-Normal is the Best Fit in Most Cases.)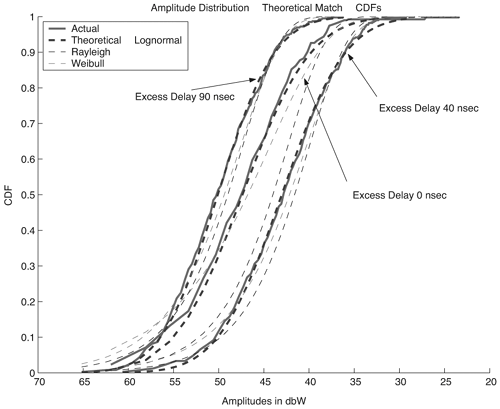 As mentioned, a unique feature of UWB channels is the large degree of time dispersion. This leads to an important metric for UWB receiver design: energy capture. The large amount of time dispersion makes high energy capture challenging. Thus, we want our channel model to reflect this behavior to allow for proper receiver design. Figure 3.26 illustrates example energy capture statistics for a RAKE receiver with a varying number of correlators corresponding to measurements of several channels [73]. It can be seen that the type of channel and the type of antenna has a large impact on energy capture. Channels with greater time dispersion require significantly more correlator resources (that is, RAKE fingers) in order to achieve the same energy capture. This must be reflected in the channel model that is used. As an example, consider a comparison of four different channel models for an NLOS channel using the bicone antennas shown in Figure 3.27. The figure plots energy capture versus the number of fingers for the Saleh-Valenzuela, Single Poisson, Split-Possion, and D-K models. Each of the models is parameterized such that they have the same average rms delay spread and mean excess delay. However, they have different energy capture statistics. For this particular data set, the Split-Poisson model matches the measurement data better than the other models. Such statistics should be considered when choosing a model, especially if a RAKE receiver architecture is being used. Figure 3.26. Total Energy Capture with Increasing Number of Rake Fingers for Example Data Sets.SOURCE: B. Donlan and R. M. Buehrer, "The UWB Indoor Channel: Large and Small-Scale Modeling," submitted to IEEE Transactions on Wireless Communications [73]. © IEEE, 2004. Used by permission. 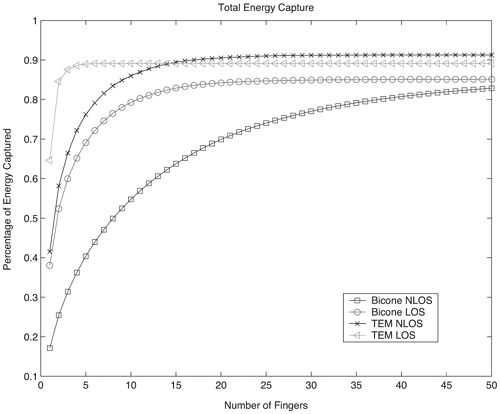 Figure 3.27. Average Cumulative Rake Finger Energy Capture for Measured Indoor Bicone NLOS Data and Various Models for Different Numbers of RAKE Fingers.SOURCE: S. Venkatesh, J. Ibrahim, and R. M. Buehrer, "A New 2-Cluster Model for Indoor UWB Channel Measurements," submitted to IEEE Transactions on Communications [76]. © IEEE, 2004. Used by permission.  3.4.10. Summary of Measurement Campaigns and Modeling EffortsA growing number of measurement campaigns and channel modeling efforts has been carried out to characterize the UWB channel. This work includes time domain and direct pulse measurements as well as frequency domain measurements using vector network analyzers. The results from the only known published measurement campaign taken in an outdoor environment are given in [48] by researchers originally at the University of Southern California and the Time Domain Corporation. The measurements were taken in a dense forest environment using a digital sampling oscilloscope as the receiver. The transmitter contains a pulse generator that creates UWB pulses with an approximate bandwidth of 1.3 GHz every 500 nanoseconds. The sampling rate of the receiver was 20.48 GHz (48.828 ps time resolution). A pulse repetition time of 500 ns was deemed sufficiently long to ensure that the multipath response of the previous pulse had decayed. Values for the mean excess delay, RMS delay spread, path loss exponents, and forestation losses are given. Outdoor results are also presented in [72]. Indoor measurements in a modern office building were taken by the same researchers using basically the same measurement system [49, 50]. Data was collected in 14 different rooms and hallways at 49 locations on a 7 x 7 square grid measuring 3 feet by 3 feet. The receive antenna was located 120 cm from the floor and 150 cm from the ceiling. Some initial analysis of the basic parameters of the channel was presented along with the measurement results. The authors and others use these results to further analyze and propose more specific channel models in several subsequent publications. Several papers [11-13] have been published offering analysis of this measurement campaign. Researchers from AT&T Labs used this data to create a model that treats channel parameters as random variables [9, 10]. The underlying model is similar to those described previously, but the variation in the model parameters from environment to environment is captured through random variables. A TH-PPM-based channel sounder developed by Time Domain Corporation was introduced in [37]. The instrument was intended to be used to develop channel models that describe large-scale attenuation (that is, path loss), the number of time resolvable multipath components, their arrival times and amplitude statistics, and the variability of propagation paths as a function of distance. The implementation described involves transmitting a 500 ps pulse (1.5 GHz bandwidth centered at 2 GHz) at a 10 MHz repetition frequency. Reference [37] uses measurements taken with this system to calculate specific channel impulse responses, path loss values, and RMS delay spread values. From their measurements, it was found that path loss and RMS delay spread both increase with distance, and the two channel metrics are highly linearly correlated (RMS delay spread was found to be more linearly correlated to path loss than distance). Intel researchers performed measurements from 2-8 GHz in residential environments. Reference [25] reports some of the results of these measurements. Some of the measurement work (performed in a townhouse) is also described in [30]. Both a time domain measurement system (digital sampling oscilloscope) and a frequency domain measurement system using a Vector Network Analyzer (VNA) were used. Researchers at IMST in Germany [51] measured office scenarios including corridor, in-office, and between offices using a VNA. The frequency sweep of the VNA was from 1 to 11 GHz. Biconical horn antennas at 1.5 m above the floor were positioned on a 150 x 30 grid (with 1 cm separation between grid points) at each measurement location. Researchers at CEA-LETI in France performed frequency domain measurements from 2-6 GHz in an office scenario for ranges up to 10 meters [3,22]. Omni-directional, conical monopole antennas were used, and the receive antenna was placed at locations on a 10 x 10 grid (with 10 cm separation between grid points) for each measurement location. Other researchers at AT&T Labs [17] report the results of measurements taken in 23 different homes using a VNA yielding over 300,000 collected power delay profiles from 712 locations in 23 homes at distances from 1 to 15 meters. Identical conical monopole antennas were used over the frequency range 4.375-5.625 GHz. Researchers at the University of Oulu in Finland [20] used a VNA to make channel measurements in a university building. Measurements were made over 2-8 GHz using conical antennas at three heights and three horizontal positions at each location. The different measurement campaigns are summarized in Table 3.11.[6]
A large set of indoor and outdoor measurements was taken by Virginia Tech as part of the DARPA NETEX program [5-7, 61, 72]. The measurements taken were both in the time domain and the frequency domain, and two types of antennas were used (bicones and TEM horns). The measurements characterized large-scale fading (discussed in Section 3.5) as well as small-scale behavior. A more detailed summary of this campaign is presented in Table 3.12.[7]
Table 3.12. Small-Scale Channel Characteristics From [72] Using 15 and 20 dB Thresholds. [View Full Width] |
|
EAN: 2147483647
Pages: 110
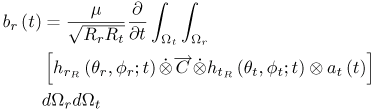

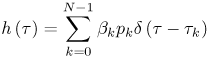
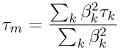

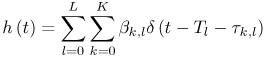
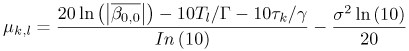


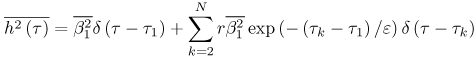
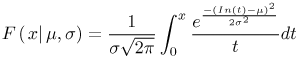
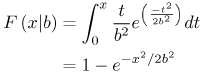
 0. The Rayleigh distribution is popular in discussing pure scattering models in the absence of a strong LOS component. It has one parameter (
0. The Rayleigh distribution is popular in discussing pure scattering models in the absence of a strong LOS component. It has one parameter (
 0 are shape and scale parameters given by
0 are shape and scale parameters given by 