40. | C++ Neural Networks and Fuzzy Logic

C++ Neural Networks and Fuzzy Logic
by Valluru B. Rao
M&T Books, IDG Books Worldwide, Inc.
ISBN: 1558515526 Pub Date: 06/01/95

Table of Contents

Outputs

The output from some neural networks is a spatial pattern that can include a bit pattern, in some a binary function value, and in some others an analog signal. The type of mapping intended for the inputs determines the type of outputs, naturally. The output could be one of classifying the input data, or finding associations between patterns of the same dimension as the input.

The threshold functions do the final mapping of the activations of the output neurons into the network outputs. But the outputs from a single cycle of operation of a neural network may not be the final outputs, since you would iterate the network into further cycles of operation until you see convergence. If convergence seems possible, but is taking an awful lot of time and effort, that is, if it is too slow to learn, you may assign a tolerance level and settle for the network to achieve near convergence.

The Threshold Function

The output of any neuron is the result of thresholding, if any, of its internal activation, which, in turn, is the weighted sum of the neuron’s inputs. Thresholding sometimes is done for the sake of scaling down the activation and mapping it into a meaningful output for the problem, and sometimes for adding a bias. Thresholding (scaling) is important for multilayer networks to preserve a meaningful range across each layer’s operations. The most often used threshold function is the sigmoid function. A step function or a ramp function or just a linear function can be used, as when you simply add the bias to the activation. The sigmoid function accomplishes mapping the activation into the interval [0, 1]. The equations are given as follows for the different threshold functions just mentioned.

The Sigmoid Function

More than one function goes by the name sigmoid function. They differ in their formulas and in their ranges. They all have a graph similar to a stretched letter s. We give below two such functions. The first is the hyperbolic tangent function with values in (–1, 1). The second is the logistic function and has values between 0 and 1. You therefore choose the one that fits the range you want. The graph of the sigmoid logistic function is given in Fig. 5.3.

1. f(x) = tanh(x) = ( e^x - e^-x) / (e^x + e^-x)

2. f(x) = 1 / (1+ e^-x)

Note that the first function here, the hyperbolic tangent function, can also be written, as 1 - 2e^-x / (e^x + e^-x ) after adding and also subtracting e^-x to the numerator, and then simplifying. If now you multiply in the second term both numerator and denominator by e^x, you get 1 - 2/ (e^2x + 1). As x approaches -∞, this function goes to -1, and as x approaches +∞, it goes to +1. On the other hand, the second function here, the sigmoid logistic function, goes to 0 as x approaches -∞, and to +1 as x approaches +∞. You can see this if you rewrite 1 / (1+ e^-x) as 1 - 1 / (1+ e^x), after manipulations similar to those above.

You can think of equation 1 as the bipolar equivalent of binary equation 2. Both functions have the same shape.

Figure 5.3 is the graph of the sigmoid logistic function (number 2 of the preceding list).

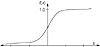
Figure 5.3 The sigmoid function.

The Step Function

The step function is also frequently used as a threshold function. The function is 0 to start with and remains so to the left of some threshold value θ. A jump to 1 occurs for the value of the function to the right of θ, and the function then remains at the level 1. In general, a step function can have a finite number of points at which jumps of equal or unequal size occur. When the jumps are equal and at many points, the graph will resemble a staircase. We are interested in a step function that goes from 0 to 1 in one step, as soon as the argument exceeds the threshold value θ. You could also have two values other than 0 and 1 in defining the range of values of such a step function. A graph of the step function follows in Figure 5.4.

Figure 5.4 The step function.

Note: You can think of a sigmoid function as a fuzzy step function.

The Ramp Function

To describe the ramp function simply, first consider a step function that makes a jump from 0 to 1 at some point. Instead of letting it take a sudden jump like that at one point, let it gradually gain in value, along a straight line (looks like a ramp), over a finite interval reaching from an initial 0 to a final 1. Thus, you get a ramp function. You can think of a ramp function as a piecewise linear approximation of a sigmoid. The graph of a ramp function is illustrated in Figure 5.5.

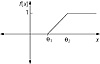
Figure 5.5 Graph of a ramp function.

Linear Function

A linear function is a simple one given by an equation of the form:

f(x) = αx + β

When α = 1, the application of this threshold function amounts to simply adding a bias equal to β to the sum of the inputs.

Applications

As briefly indicated before, the areas of application generally include auto- and heteroassociation, pattern recognition, data compression, data completion, signal filtering, image processing, forecasting, handwriting recognition, and optimization. The type of connections in the network, and the type of learning algorithm used must be chosen appropriate to the application. For example, a network with lateral connections can do autoassociation, while a feed-forward type can do forecasting.

Some Neural Network Models

Adaline and Madaline

Adaline is the acronym for adaptive linear element, due to Bernard Widrow and Marcian Hoff. It is similar to a Perceptron. Inputs are real numbers in the interval [–1,+1], and learning is based on the criterion of minimizing the average squared error. Adaline has a high capacity to store patterns. Madaline stands for many Adalines and is a neural network that is widely used. It is composed of field A and field B neurons, and there is one connection from each field A neuron to each field B neuron. Figure 5.6 shows a diagram of the Madaline.

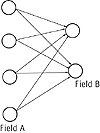
Figure 5.6 The Madaline model.

Table of Contents