DATA CUBES FOR INVERTIBLE AGGREGATE OPERATORS

Our research is mainly concerned with invertible aggregate operators, i.e., where the inverse of a value is well defined and unique. More precisely, an operator is invertible if the domain of the measure attribute forms an abelian group under the operator. Popular examples are important SQL operators like SUM, COUNT, and AVG (when expressing it with SUM and COUNT). The existence of inverse operations enables the construction of elegant techniques for speeding up queries on MOLAP data cubes that do not require additional storage compared to materializing the original cube.

We will also explain the techniques for the operator SUM. Other invertible operators are handled in a similar way. Let A denote the original data cube. The unit of cost used is the number of cells accessed by an operation. Hence, updating a single cell in A results in a cost of 1. A range query Q that selects range r_i of size |r_i| in dimension i has a cost of , i.e., a worst-case cost of . Using A for OLAP represents a perfectly dynamic solution, but incurs high query costs.

Achieving Constant Query Costs

In a query-dominated environment, simply storing A is not the best choice. In the worst case all the cells of A have to be accessed in order to answer a range query. On the other hand the query only outputs a single aggregate value, the sum over all selected cells.

Ho et al. (1997) addressed this issue with their Prefix Sum (PS) technique. The main idea is to use a prefix sum cube PS instead of A. Each cell PS[c₁, …, c_d] contains the corresponding prefix sum Based on the principle of inclusion-exclusion, each range sum query on A can be computed from up to 2^d corresponding prefix sums. Figure 2 shows an original data cube A and the corresponding PS cube. The cells accessed by query SUM(A[4, 2] : A[6, 5]) are shaded. Consider the lower right corner PS[6, 5] in PS. The value represents the sum over all cells in A that are dominated by, i.e., to the upper left of, cell A[6, 5]. Hence, to answer the range query, the upper right (PS[3, 5]) and lower left (PS[6,1]) cells need to be subtracted. This causes the cells in A[0, 0] : A[3,1] to be removed twice, therefore the upper left cell PS[3, 1] must be added. This approach can be easily generalized to higher dimensionality (see Ho et al., 1997). Consequently, the worst-case query cost using PS is reduced to 2^d which is independent of the size of the data cube and the size of the query region. At the same time the update cost increases dramatically. An update to a cell A[c] affects all cells PS[x] that dominate c, i.e., all cells x where x_i ≥ c_i for all dimensions i. In the worst case the whole PS cube could be affected.

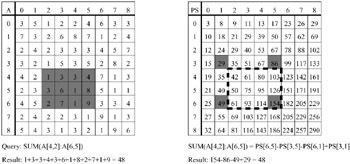
Figure 2: Original Data Cube A and Corresponding Prefix Cube PS with Range Sum Query

To avoid PS's expensive cascading updates, Geffner et al. (in Geffner, Agrawal, El Abbadi, & Smith, 1999, and in Geffner, Riedewald, Agrawal, & El Abbadi, 1999), introduced the Relative Prefix Sum (RPS). In this chapter we present a later version of RPS which removed RPS's initial unnecessary storage overhead and appeared in Riedewald, Agrawal, El Abbadi, and Rajarola (2000). RPS retains the constant query time but considerably reduces the update cost by removing some of the dependencies of the pre-aggregated values. The technique conceptually partitions A into smaller hyper-rectangular chunks, called boxes. Essentially inner cells of a box store prefix sums local to the box, while the border cells in selected surfaces also aggregate outside values. Figure 3 shows examples for aggregation regions of box cells. Note that any prefix range query can be answered by accessing up to 2^d cells (2^d − 1 border cells, 1 inner cell) in the box the endpoint of the query-region falls into.

Figure 3: Aggregation Regions of Cells for RPS

Figure 4 shows an example for an RPS cube and how a prefix sum can be partitioned such that the corresponding box values provide the result. Compared to the PS technique, more values are accessed to obtain a prefix sum, but it is still much less costly than adding the values of the original data cube on-the-fly. Arbitrary range sum queries are answered by combining up to 2^d prefix sums as for the PS technique. The cascading updates are restricted to the box that contains the updated cell. Outside the box only some of the border cells of other boxes are affected, as shown for an example in Figure 4. It can be shown analytically that the optimal tradeoff between query and update costs occurs when the side-length of a box is chosen to be in dimension i. Then the worst-case costs are 4^d for queries and for updates. Note that PS is a special case of RPS when boxes of size 1 are selected.

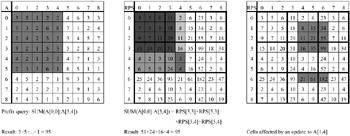
Figure 4: Original Data Cube A and Corresponding RPS Cube with Range Sum Query (Middle) and Update (Right)

Making the Cubes More Dynamic

For environments with high update volumes, Geffner, Agrawal and El Abbadi (2000) propose a technique that balances query and update costs such that they are both polylogarithmic in the data size. However, the original proposal resulted in considerable storage overhead. This overhead was removed by Riedewald, Agrawal, El Abbadi, and Pajarola (2000). We present an overview of the latter approach which will be referred to as the Dynamic Data Cube (DDC).

Like RPS, DDC conceptually partitions the original cube into boxes and uses the same aggregation regions for a box's border cells. However, the number of boxes is bounded by a constant (e.g., divide each dimension in half). Hence the side-length of a box is linear in the domain size. For inner box cells a recursive approach is taken. To be more specific, the same partitioning into boxes is recursively applied to the region of inner box cells. As defined so far, the cumulative nature of the border cells in a box would still lead to high update costs. Interestingly, a recursive encoding similar to the inner cells solves the problem.

The recursive DDC approach defines a hierarchy. Queries and updates are processed by conceptually descending this tree. If the recursive box partitioning always divides boxes in half, then the technique guarantees worst-case costs of and for queries and updates, respectively. The main disadvantage is that, due to its recursive nature, the technique is not easy to analyze (e.g., for average costs) and to implement. Figure 5 shows a DDC cube; in Figure 6 the tree structure is illustrated, along with how a query is processed.

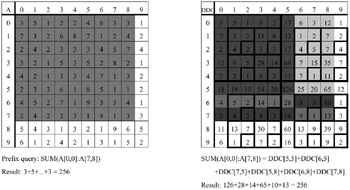
Figure 5: Original Data Cube A and Corresponding DDC Cube with Range Sum Query

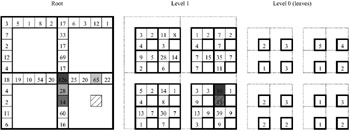
Figure 6: Tree Structure of the DDC Cube (Query Endpoint Hatched, Accessed Cells Shaded)

Offering Multiple Query-Update Tradeoffs

Chan and Ioannidis (1999) are the first to explicitly explore the possibility of letting the user choose a query-update tradeoff by parameterizing the construction of the pre-aggregated cube. They apply ideas from bitmap index design and define an interesting class of so-called Hierarchical Cubes (HCs). Like for DDC the data cube is hierarchically partitioned into smaller boxes of equal size. According to the partitioning, the cells are assigned to classes. Two techniques, Hierarchical Rectangle Cubes (HRCs) and Hierarchical Band Cubes (HBCs) are proposed that define aggregation regions for the cells depending on their classes. Having different hierarchical partitionings and different ways of assigning aggregation regions, a variety of tradeoffs between query and update cost can be generated. Figure 7 shows an example for HBC when each dimension is recursively split in half. The shading in the middle cube indicates the level of each cell (darkest at root level). The right cube indicates how the query result is obtained as the sum of two pre-computed values that are the range sums for the corresponding regions. Explicit cost formulas enable an analyst to choose the right HBC or HRC parameter setting for an application. However, the formulas are quite complex (cf., Chan & Ioannidis, 1999). Finding good configurations therefore requires an experimental evaluation.

Figure 7: Original Data Cube A and a Possible HBC Cube

Combining Efficiency, Flexibility, and Simplicity

RPS, DDC, and HC are sophisticated multidimensional pre-aggregation techniques. Hence the corresponding algorithms are typically complex (cf., Chan & Ioannidis, 1999; Geffner, Agrawal, & El Abbadi, 2000), and it is difficult to prove their correctness and to analyze their performance. The different dimensions of a data cube are treated uniformly in the sense that even though box sizes might vary, the same general scheme is used for each dimension. However, in practice attributes have very diverse characteristics. For instance, the gender attribute of a census data set has only two possible values, while income covers a large range. For some attributes a priori semantic information makes one aggregation technique preferable over another. For instance, when a natural hierarchy exists for an attribute, users typically query according to this hierarchy (e.g., it is more likely that a query aggregates monthly sales figures than sales figures for some 30-day period that starts on the third of a month). For such dimension attributes DDC with its hierarchical aggregation structure could be the technique of choice. For another attribute PS or HBC might be better.

This is the motivation behind the iterative data cubes (IDCs) proposed by Riedewald et al. (2001). The approach provides a modular framework for combining one-dimensional pre-aggregation techniques to create space-optimal multidimensional pre-aggregated data cubes. By selecting the appropriate one-dimensional techniques, the specific properties of the dimensions can be taken into account. Not only can the advantages of different pre-aggregation schemes be combined within a single cube, also the overall cost functions can easily be obtained based on the corresponding one-dimensional costs. Hence, analyzing and implementing a d-dimensional IDC is essentially reduced to the one-dimensional case. When a new dimension attribute with specific properties is to be included into the framework, all one has to do is develop a new one-dimensional pre-aggregation approach for it.

For the following discussion let Θ be a one-dimensional pre-aggregation technique and A be a one-dimensional array with N cells. Technique Θ generates a pre-aggregated array A_Θ of size N, such that each cell of A_Θ stores a linear combination of the cells of A:

The values of the variables α_j,k are determined by the pre-aggregation technique. Figure 8 shows an example. The array RPS is the result of applying the RPS technique with block size 3 to the original array A. RPS pre-aggregates a one-dimensional array as follows. A is partitioned into blocks of equal size. The anchor of a block a : e (its leftmost cell) contains the corresponding prefix sum of A, i.e., RPS[a] = SUM (A[0] : A[a]). Any other cell c of the block stores the "local prefix sum" RPS[c] = SUM(A[a + 1] : A[c]). Consequently, the coefficients α_j,k in the example are α _0,0 = 1, α_1,1 = 1, α _2,1 = 1, α_3,k = 1 for 0 ≤ k ≤ 3, α _4,4 = 1, α_5,4 = α_5,5 = 1, α_6,k = 1 for 0 ≤ k ≤ 6, and α_j,k, = 1 for all other combinations of j and k.

Figure 8: Original Array A and Corresponding RPS (Block Size 3) and PS Arrays (Query Range and Updated Cell in A Are Framed, Accessed Cells Are Shaded)

To construct an IDC for a d-dimensional original data cube A, a pre-aggregation technique Θ_i is selected for each dimension i. First each one-dimensional vector A[0, x₂, x₃,…, x_d] : A [N₁, x₂, x₃,..., x_d], x_i ∊ {0, 1,..., N_i} for 2 ≤ i ≤ d, is processed with technique Θ₁. Let the result be cube A₁.A₁ is then processed similarly, applying technique Θ₂ to all vectors along dimension 2, and so on. Interestingly, if PS is selected for each dimension, the final IDC cube is identical to the d-dimensional PS cube. The same holds for using RPS and DDC for all dimensions. However, IDC can also combine these and other techniques. For example for a three-dimensional data set, one could select PS for the first, DDC for the second, and HBC for the third dimension. Figure 9 shows how the RPS cube from Figure 4 is constructed using the IDC approach. First A's rows are processed using one-dimensional RPS, then the columns of the intermediate result are processed with RPS as well.

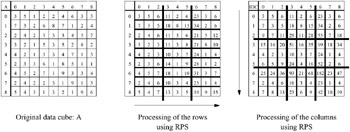
Figure 9: Original Data Cube A, Intermediate Result, and Final IDC Cube (Fat Lines Indicate Partitioning into Blocks by RPS)

A nice property of IDC is that the query and update algorithms for a d-dimensional data cube also can be obtained as a simple combination of the one-dimensional algorithms. The designer of a one-dimensional pre-aggregation technique only has to ensure that the technique is reversible. Let A be a one-dimensional array, Θ be a one-dimensional pre-aggregation technique, and A_Θ be the resulting pre-aggregated array. Θ is reversible if and only if for each range r = A[i] :A[j], 0 ≤ i ≤ j ≤ N, there are variables β_r,l such that SUM (A[i] : In other words, the pre-aggregation technique has to guarantee that each range sum on A can still be computed on A_Θ. A range query on a d-dimensional original data cube A is then translated to a query on the IDC cube by determining the relevant cells (those with non-zero betas) for each dimension. Note, that there are no inter-dimensional dependencies, i.e., the betas in a dimension only depend on the technique used and the range selected in this dimension. The update process is similar.

Figure 10 shows an example for a query that computes SUM(A[4, 2] : A[6,6]) on the IDC cube from Figure 9. For range 4 : 6 in dimension 1 and range 2 : 6 in dimension 2, the indices with non-zero beta values are obtained together with the betas. For instance for range 2 : 6 in dimension 2, the relevant indices are 0, 1, and 6 with beta values of -1, -1, and 1, respectively (see also RPS query translation in Figure 8). Similarly, for dimension 1 the indices 3 and 6 with beta values of -1 and 1 are obtained. Note that selecting a different pre-aggregation technique or query range in dimension 2 would not affect the indices or beta values in dimension 1, and vice versa. Combining the one-dimensional results is straightforward. The relevant indices in the d-dimensional cube are the combinations of the one-dimensional result sets. The beta values are multiplied (for details see Riedewald, Agrawal, & El Abbadi, 2001).

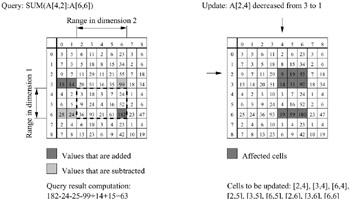
Figure 10: Processing Queries and Updates on an Iterative Data Cube (RPS Technique Used for Both Dimensions)

The query and update costs for a d-dimensional IDC cube are the product of the numbers of non-zero betas in each dimension. Hence, for example, the worst-case query cost of an IDC cube is the product of the worst-case query costs of the one-dimensional pre-aggregation techniques used for its dimensions. Table 1 shows a selection of techniques with their respective worst-case costs for vectors with N_i elements.

Table 1: Query-Update Cost Tradeoffs for Selected One-Dimensional Techniques

One-dimensional technique	Query cost (worst case)	Update cost (worst case)
Original Array	Ni	1
Prefix Sum (PS)	2	Ni
Relative Prefix Sum (RPS)	4
Dynamic Data Cube (DDC)	2log2Ni	log2Ni

The possibility of combining arbitrary, one-dimensional pre-aggregation techniques allows users to generate a great variety of IDC instances. Their query and update characteristics are given by simple formulas. For instance, if PS and RPS are used for dimensions 1 and 2 of a two-dimensional data cube, the worst-case query and update costs are 8 and , respectively. If DDC and PS are used, the costs are 4log₂N₁ and log₂N₁, respectively.

Note that this simplicity and flexibility comes at the cost of a restriction of the solution space compared to arbitrary multidimensional pre-aggregation techniques. However, it can be shown that IDC either matches or improves the query-update tradeoffs of previously proposed techniques. PS, RPS, and DDC are special cases of IDC.