BACKGROUND

The term "data cube" is not used consistently in the data warehousing research literature. We will use the following rather general definition. A data set is conceptually modeled as a multidimensional hyper-rectangle, or data cube for short. The d functional attributes that describe a data item in the set are the dimensions. Some of them are hierarchical, e.g., year-quarter-month-day for the time dimension (sometimes multiple hierarchies for an attribute exist, e.g., week-day is another hierarchy for the time dimension). A d-tuple of dimension values defines a cell of the data cube, similar to a multidimensional array. Cells contain the values of additional attributes, the measure attributes. For simplicity and without loss of generality, we will further on assume that the cube has only a single measure attribute.

Note that we do not advocate any particular implementation for data cubes. Possible solutions were examined elsewhere, e.g., in Goil & Choudhary (1997), Roussopoulos, Kotidis, & Roussopoulos (1997), and Sarawagi & Stonebraker (1994). The model is also not restricted to a certain OLAP architecture like Multidimensional OLAP (MOLAP) or Relational OLAP (ROLAP) (for a discussion of ROLAP and MOLAP, see Pendse & Creeth, 2001). However, our discussion will mainly focus on MOLAP techniques.

A simple example is a sales data cube with dimensions product, time (date of sale), and location (place of sale), and the measure attribute amount (value of sales transaction). Hence for each product, time, and location, the corresponding amount of sales is stored. Figure 1 shows a possible instance with dimension hierarchies indicated (ALL represents the whole domain of an attribute). If there is no sales transaction for a certain combination of dimension values, the corresponding cell is empty. In the figure empty cells contain the value 0.

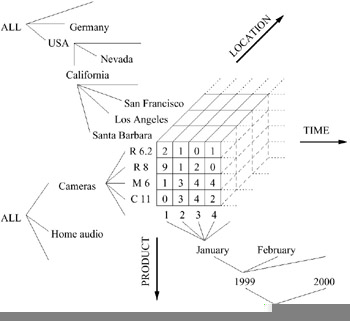
Figure 1: Data Cube Example

As summarized in Chaudhuri & Dayal (1997), dominant aggregate query types on data cubes are roll-up/drill-down (increases, respectively decreases, level of aggregation along one or more attribute hierarchies) and slice-and-dice (selects attributes and cells of interest).

These queries are typically range queries or sequences of related range queries (e.g., hierarchical range queries as discussed in Koudas, Muthukrishnan, & Srivastava, 2000). Hence, we are mainly concerned with support for aggregate range queries which select a hyper-rectangular region of the data cube and return an aggregate, e.g., SUM or COUNT, of the measure values of the selected cells. A formal definition is given below.

Let A denote a d-dimensional data cube such that dimension i (1 ≤ i ≤ d) has N_i cells. Without loss of generality, let the domain of dimension i be {0,1,…, N_i -1}. A cell c = [c_l,…, c_d], where each c_i is an element of the domain of the corresponding dimension, contains the measure value A[c]. With e:f we denote a hyper-rectangular region of the data cube, more precisely the set of all cells c that satisfy e_i ≤ c_i ≤ f_i for all 1 ≤ i ≤ d. Cell e is the anchor and cell f the endpoint of the region. The anchor and endpoint of the entire data cube hence are [0,…, 0] and [N₁ - 1,…, N_d- 1], respectively. The term op(A[e] : A[f]) denotes the result of applying the aggregate operator op to the measure values in region e : f, i.e., it defines an aggregate range query. For example, SUM(A[e] : A[f]) is a range sum. The range sum SUM(A[0,…, 0] : A[f]) will be referred to as a prefix sum.

The term original cube denotes a data cube which is obtained as the straightforward projection of a data set to the d-dimensional space defined by the cube's dimensions. If any of the cube's cells contain values which are aggregates of multiple cells of an original cube (e.g., sub-totals), it will be referred to as a preaggregated cube.