Bayesian Approach

---

Given a set of forecasts from different methods, we regard the values as sample points from a density. Since at each time we only have a few forecast values, therefore a classical approach for mode estimate seems to be inappropriate. A Bayesian approach is therefore considered. Here we assume that the forecast values do not follow a Gaussian distribution and we assume that it follows the Weibull distribution. This assumption is supported by the empirical evidence. The Weibull distribution is a commonly used distribution in many applications when the density is assumed to be non-Gaussian (see Kotz and Johnson [1988] and the references therein).

We say that a random variable X follows the two-parameter Weibull distribution, denoted as We(a,b), if the density function and the cumulative distribution function are:

(14)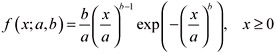 

(15)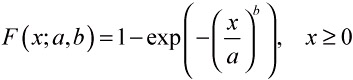 

The log-likelihood function is given by

(16)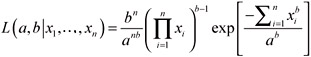 

The parameter b(b > 0) is a dimensionless shape parameter and a(a > 0) is a scale parameter with the same dimension as X. For a Bayesian approach, we need to choose a joint prior distribution for parameter a and b. As we lack information about this density, we choose the joint prior distribution inversely proportional to the scale parameter a. That is, the joint prior distribution . Then the joint posterior is

(17)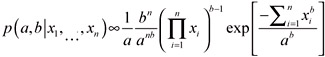 

It can be shown that the joint posterior distribution and the marginal posterior distribution a and b are proper posterior densities. Therefore important statistics about the parameters such as the posterior mode can be obtained by using the proper joint posterior distribution in equation (17).

---