Recipe 6.34. Solving Simultaneous Equations

Problem

You want to solve a set of n simultaneous equations containing n unknowns.

Solution

Sample code folder: Chapter 06\Matrix

Use the matrix operations presented in the MatrixHelper module to solve the equation.

Discussion

Matrices are useful in solving simultaneous equations. The solution is defined in Cramer's Rule, a theorem of linear algebra named after mathematician Gabriel Cramer. (A full description of matrices and their operations is beyond the scope of this book.)

The MatrixHelper module contains a special-purpose function that solves simultaneous equations by calling several matrix-analysis functions. You pass a square matrix of size n containing the coefficients of the unknowns from the equations, along with a one-dimensional array containing the equation constants. The MatrixHelper.SimultEq() function then returns a one-dimensional array containing the solution values for the equation's unknowns. Here is the code listing for the MatrixHelper.SimultEq() function:

 Public Function SimultEq( _      ByVal sourceEquations(,) As Double, _      ByVal sourceRHS() As Double) As Double()    ' ----- Use matrices to solve simultaneous equations.    Dim rowsAndCols As Integer    ' ----- The matrix must be square and the array size    '       must match.    Dim rank As Integer = UBound(sourceEquations, 1)    If (UBound(sourceEquations, 2) <> rank) Or _          (UBound(sourceRHS, 1) <> rank) Then       Throw New Exception( _          "Size problem for simultaneous equations.")    End If    ' ----- Create some arrays for doing all of the work.    Dim coefficientMatrix(rank, rank) As Double    Dim rightHandSide(rank) As Double    Dim solutions(rank) As Double    Dim rowPivots(rank) As Integer    Dim colPivots(rank) As Integer    ' ----- Make copies of the original matrices so we don't    '       mess them up.    Array.Copy(sourceEquations, coefficientMatrix, _       sourceEquations.Length)    Array.Copy(sourceRHS, rightHandSide, sourceRHS.Length)    ' ----- Use LU decomposition to form a triangular matrix.    coefficientMatrix = FormLU(coefficientMatrix, _       rowPivots, colPivots, rowsAndCols)    ' ----- Find the unique solution for the upper-triangle.    BackSolve(coefficientMatrix, rightHandSide, solutions, _       rowPivots, colPivots)    ' ----- Return the simultaneous equations result in    '       an array.    Return solutions End Function 

For example, say you have a pile of 18 coins comprised of pennies, nickels, dimes, and quarters totaling $2.23. The nickels and dimes total $.70, and the dimes and quarters total $2.00. The unknowns are the numbers of each of the four types of coins. The given information provides all you need to solve a set of four equations with four unknowns:

P + N + D + Q + = 18

P + 5N + 10D + 25Q = 223

0P + 5N + 10D + 0Q= 70

0P + 0N + 10D + 25Q= 200

The following code sets up the 4 x 4 matrix of coefficients and the array of constants, then passes these two arrays to MatrixHelper.SimultEq() to solve for the four unknowns:

 Dim matrixA(,) As Double = { _    {1, 1, 1, 1}, _    {1, 5, 10, 25}, _    {0, 5, 10, 0}, _    {0, 0, 10, 25}} Dim arrayB() As Double = {18, 223, 70, 200} Dim arrayC() As Double = _    MatrixHelper.SimultEq(matrixA, arrayB) MsgBox(MatrixHelper.MakeDisplayable(matrixA) & vbNewLine & _    vbNewLine & MatrixHelper.MakeDisplayable(arrayB) & _    vbNewLine & vbNewLine & _    "Simultaneous Equations Solution:" & _    vbNewLine & MatrixHelper.MakeDisplayable(arrayC)) 

As shown by the results displayed in Figure 6-34, there are three pennies, four nickels, five dimes, and six quarters in the pile.

Figure 6-34. Solving a set of four equations with four unknowns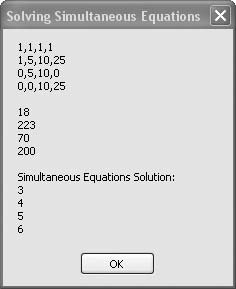

The MatrixHelper.SimultEq() function is listed in the MatrixHelper module code, presented in the next recipe.

See Also

See the full MatrixHelper.vb listing in Recipe 6.35.