Brainteaser Problems

Brainteasers draw from a much broader and more diverse body of knowledge than programming and technical problems, so a comprehensive review isn’t possible here. The following brainteasers will hone your problem-solving skills in preparation for an interview.

Count Open Lockers

Important 

Suppose you are in a hallway lined with 100 closed lockers. You begin by opening all 100 lockers. Next, you close every second locker. Then you go to every third locker and close it if it is open or open it if it is closed (call this toggling the locker). You continue toggling every nth locker on pass number n. After your hundredth pass of the hallway, in which you toggle only locker number 100, how many lockers are open?

In a hall with k lockers, how many lockers remain open after pass k?

This problem is designed to seem overwhelming. You don’t have time to draw a diagram of 100 lockers and count 100 passes through them. Even if you did, solving the problem that way wouldn’t illustrate any skill or intuition, so there must be some trick that can be used to determine how many doors will be open. You just have to figure out what that trick is.

It’s unlikely that you’re going to be able to intuit the solution to this problem by just staring at it. What can you do? Although it’s not practical to solve the entire problem by brute force, solving a few lockers in this manner is reasonable. Perhaps you’ll notice some patterns you can apply to the larger problem.

Start by choosing an arbitrary locker, 12, and determining whether it will end open or closed. On which passes will you toggle locker 12? Obviously on the first pass, when you toggle every locker, and on the twelfth pass when you start with 12. You don’t need to consider any pass after 12 because those will all start farther down the hall. This leaves passes 2 through 11. You can count these out: 2, 4, 6, 8, 10, 12 (you toggle on pass 2); 3, 6, 9, 12 (on 3); 4, 8, 12 (on 4); 5, 10, 15 (not on 5); 6, 12 (on 6); 7, 14 (not on 7), and so on. Somewhere in the middle of this process, you will probably notice that you toggle locker 12 only when the number of the pass you’re on is a factor of 12. If you think about this, it makes sense: When counting by n, you hit 12 only when some integer number of n’s add to 12, which is another way of saying that n is a factor of 12. Though it seems simple in retrospect, this probably wasn’t obvious before you worked out an example.

The factors of 12 are 1, 2, 3, 4, 6, and 12. Correspondingly, the operations on the locker door are open, close, open, close, open, close. So locker 12 will end closed. The solution seems to have something to do with factors. Primes are numbers with unique factor properties. Perhaps it would be instructive to investigate a prime numbered locker. You might select 17 as a representative prime. The factors are 1 and 17, so the operations are open, close. It ends closed just like 12. Apparently primes are not necessarily different from nonprimes for the purposes of this problem.

What generalizations can you make about whether a locker ends open or closed? All lockers start closed and alternate between being open and closed. So lockers are closed after the second, fourth, sixth, and so on, times they are toggled - in other words, if a locker is toggled an even number of times, then it ends closed; otherwise, it ends open. You know that a locker is toggled once for every factor of the locker number, so you can say that a locker ends open only if it has an odd number of factors.

The task has now been reduced to finding how many numbers between 1 and 100 have an odd number of factors. The two you’ve examined (and most others, if you try a few more examples) have even numbers of factors. Why is that? If a number i is a factor of n, what does that mean? It means that i times some other number j is equal to n. Of course, because multiplication is commutative (i × j = j × i), that means that j is a factor of n, too, so the number of factors is usually even because factors tend to come in pairs. If you can find the numbers that have unpaired factors, you will know which lockers will be open. Multiplication is a binary operation, so two numbers will always be involved, but what if they are both the same number (that is, i = j)? In that case, a single number would effectively form both halves of the pair and there would be an odd number of factors. When this is the case, i × i = n. Therefore, n would have to be a perfect square. Try a perfect square to check this solution. For example, for 16, the factors are 1, 2, 4, 8, 16; operations are open, close, open, close, open - as expected, it ends open.

Based on this reasoning, you can conclude that only lockers with numbers that are perfect squares end open. The perfect squares between 1 and 100 (inclusive) are 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100. So 10 lockers would remain open.

Similarly, for the general case of k lockers, the number of open lockers is the number of perfect squares between 1 and k, inclusive. How can you best count these? The perfect squares themselves are inconvenient to count because they’re unevenly spaced. However, the square roots of the perfect squares greater than zero are the positive integers. These are very easy to count: The last number in the list of square roots gives the number of items in each list. For example, the square roots of 1, 4, 9, 16, and 25 are 1, 2, 3, 4, and 5; the last number in the list of square roots is the square root of the largest perfect square and is equal to the number of perfect squares. You need to find the square root of the largest perfect square less than or equal to k.

This task is trivial when k is a perfect square, but most of the time it won’t be. In these cases, the square root of k will be a noninteger. If you round this square root down to the nearest integer, then its square is the largest perfect square less than k-just what you were looking for. The operation of rounding to the largest integer less than or equal to a given number is often called floor. Thus, in the general case of k lockers, there will be floor(sqrt(k)) lockers remaining open.

The key to solving this problem is trying strategies to solve parts of the problem even when it isn’t clear how these parts will contribute to the overall solution. Although some attempts, such as the investigation of prime numbered lockers, may not be fruitful, others are likely to lead to greater insight about how to attack the problem, such as the strategy of calculating the result for a single locker. Even in the worst case, where none of the things you try lead you closer to the final solution, you show the interviewer that you aren’t intimidated by difficult problems with no clear solution and that you are willing to keep trying different approaches until you find one that works.

Three Switches

Important 

You are standing in a hallway next to three light switches, all of which are off. Each switch operates a different incandescent light bulb in the room at the end of the hall. You cannot see the lights from where the switches are. Determine which light corresponds to each switch. You may go into the room with the lights only once.

The crux of this problem comes quickly to the fore: There are only two possible positions for each switch (on or off) but there are three lights to identify. You can easily identify one light, by setting one switch differently than the other two, but this leaves you no way to distinguish the two left in the same position.

When confronted with a seemingly impossible task, you should go back to basics. The two key objects in this problem seem to be the switches and the lights. What do you know about switches and light bulbs? Switches make or break an electrical connection. When a switch is on, current flows through it. A light bulb consists of a resistive filament inside an evacuated glass bulb. When current flows through the filament, it consumes power, producing light and heat.

How can these properties help you solve the problem? Which of them can you detect or measure? The properties of a switch don’t seem too useful. It’s much easier to look at the switch to see whether it’s off or on than to measure current. The light bulbs sound a little more promising. You can detect light by looking at the bulbs, and you can detect heat by touching them. Whether there is light coming from a bulb is determined entirely by its switch - when the switch is on, there is light; when it’s off, there isn’t. What about heat? It takes some time for a light to heat up after it’s been switched on, and some time for it to cool after it’s switched off, so you could use heat to determine whether a bulb had been on, even if it were off when you walked into the room.

You can determine which switch goes with each bulb by turning the first switch on and the second and third off. After ten minutes, turn the first switch off, leave the second off, and turn the third on. When you go into the room, the hot dark bulb corresponds to the first switch, the cold dark bulb to the second, and the lit bulb to the third.

Although there’s nothing truly outlandish about this question - it’s not just a stupid play on words, for instance - it is arguably a trick question. The solution involves coming up with something somewhat outside the definition of the problem. Some interviewers believe that questions like this will help them identify people who can “think outside the box” and develop nontraditional, innovative solutions to difficult problems. In the authors’ opinion, these problems are cheap shots that don’t prove much of anything. Nevertheless, these problems do appear in interviews, and you should be prepared for them.

Bridge Crossing

Important 

A party of four travelers comes to a rickety bridge at night. The bridge can hold the weight of at most two of the travelers at a time, and it cannot be crossed without using a flashlight. The travelers have one flashlight among them. Each traveler walks at a different speed: The first can cross the bridge in 1 minute, the second in 2 minutes, the third in 5 minutes, and the fourth takes 10 minutes to cross the bridge. If two travelers cross together, they walk at the speed of the slower traveler.

What is the least amount of time in which all the travelers can cross from one side of the bridge to the other?

Because there is only one flashlight, each trip to the far side of the bridge (except the last trip) must be followed by a trip coming back. Each of these trips consists of either one or two travelers crossing the bridge. To get a net movement of travelers to the far side of the bridge, you probably want to have two travelers on each outbound trip and one on each inbound trip. This strategy gives you a total of five trips, three outbound and two inbound. Your task is to assign travelers to the trips so that you minimize the total time for the five trips. For clarity, you can refer to each traveler by the number of minutes it takes him to cross the bridge.

Number 1 can cross the bridge at least twice as fast as any of the other travelers, so you can minimize the time of the return trips by always having 1 bring the flashlight back. This suggests a strategy whereby 1 escorts each of the other travelers across the bridge one by one.

One possible arrangement of trips using this strategy is illustrated in Figure 12-1. The order in which 1 escorts the other travelers doesn’t change the total time: The three outbound trips have times of 2, 5, and 10 minutes, and the two inbound trips are 1 minute each, for a total of 19 minutes.

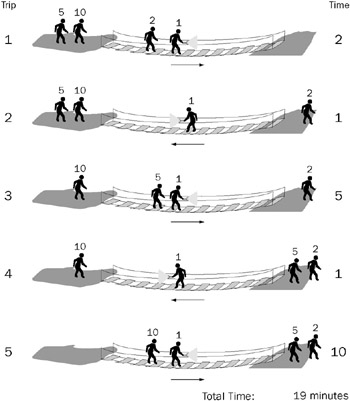
Figure 12-1

This solution is logical, obvious, and doesn’t take long to discover. In short, it can’t possibly be the best solution to an interview problem. Your interviewer would tell you that you can do better than 19 minutes, but even without that hint you should guess you arrived at the preceding solution too easily.

This puts you in an uncomfortable, but unfortunately not unusual, position. You know your answer is wrong, yet based on the assumptions you made, it’s the only reasonable answer. It’s easy to get frustrated at this point. You may wonder if this is a trick question: Perhaps you’re supposed to throw the flashlight back or have the second pair use a lantern. No such tricks are necessary here. A more-efficient arrangement of trips exists. Because the only solution that seems logical is wrong, you must have made a false assumption.

Consider your assumptions, checking each one to see if it might be false. First among your assumptions was that outbound and inbound trips must alternate. This seems correct - there’s no way to have an outbound trip followed by another outbound trip because the flashlight would be on the wrong side of the bridge.

Next, you assumed that there would be two travelers on each outbound trip and one on each return trip. This seems logical, but it’s harder to prove. Putting two travelers on an inbound trip seems terribly counterproductive; after all, you’re trying to get them to the far side of the bridge. An outbound trip with only one traveler is potentially more worthwhile, but coupled with the requisite return trip all it really accomplishes is exchanging the positions of two travelers. Exchanging two travelers might be useful, but it will probably waste too much time to be worth it. Because this possibility doesn’t look promising, try looking for a false assumption elsewhere and reconsider this one if necessary.

You also assumed that 1 should always bring the flashlight back. What basis do you have for this assumption? It minimizes the time for the return trips, but the goal is to minimize total time, not return trip time. Perhaps the best overall solution does not involve minimized return trip times. The assumption that 1 should always return the flashlight seems hard to support, so it probably merits further examination.

If you’re not going to have 1 make all the return trips, then how will you arrange the trips? You might try a process of elimination. You obviously can’t have 10 make a return trip, because then he’d have at least three trips, which would take 30 minutes. Even without getting the remaining travelers across, this is already worse than your previous solution. Similarly, if 5 makes a return trip then you have two trips that are at least 5 minutes, plus one that takes 10 minutes (when 10 crosses). Just those three trips total 20 minutes, so you won’t find a better solution by having 5 make a return trip.

You might also try analyzing some of the individual trips from your previous solution. Because 1 escorted everyone else, there was a trip with 1 and 10. In a sense, when you send 1 with 10, 1’s speed is wasted on that trip because the crossing still takes 10 minutes. Looking at that from a different perspective, any trip that includes 10 always takes 10 minutes, no matter which other traveler goes along. Therefore, if you’re going to have to spend 10 minutes on a trip, you might as well take advantage of it and get another slow traveler across. This reasoning indicates that 10 should cross with 5, rather than with 1.

Using this strategy, you might begin by sending 10 and 5 across. However, one of them has to bring the flashlight back, which you already know isn’t the right solution. You’ll want to already have someone faster than 5 waiting on the far side. Try starting by sending 1 and 2 across. Then have 1 bring the flash-light back. Now that there’s someone reasonably fast (2) on the far side, you can send 5 and 10 across together. Then 2 returns the flashlight. Finally, 1 and 2 cross the bridge again. This scheme is illustrated in Figure 12-2.

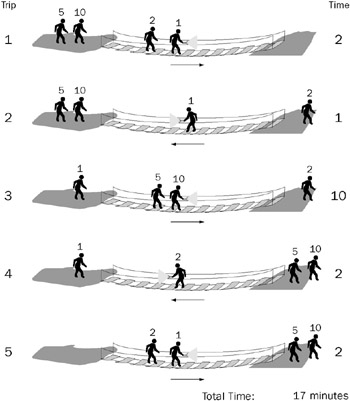
Figure 12-2

The times for the respective trips under this strategy are 2, 1, 10, 2, and 2, for a total of 17 minutes. Identifying the false assumption improved your solution by 2 minutes.

This problem is a slightly unusual example of a class of problems involving optimizing the process of moving a group of items a few at a time from one place to another. More commonly, the goal is to minimize the total number of trips, and there are often restrictions on which items can be left together. This particular problem is difficult because it suggests a false assumption (that 1 should escort each of the other travelers) that seems so obvious you may not even realize you’re making an assumption.

Heavy Marble

Important 

You have eight marbles and a two-pan balance. All the marbles weigh the same, except for one, which is heavier than all the others. The marbles are otherwise indistinguishable. You may make no assumptions about how much heavier the heavy marble is. What is the minimum number of weighings needed to be certain of identifying the heavy marble?

The first step in solving this problem is to realize that you can put more than one marble in each pan of the balance. If you have equal numbers of marbles in each pan, then the heavy marble must be in the group on the heavy side of the balance. This saves you from having to weigh each marble individually, and it enables you to eliminate many marbles in a single weighing.

Once you realize this, you are likely to devise a binary search-based strategy for finding the heavy marble. In this method, you begin by putting half of the marbles on each side of the balance. Then you eliminate the marbles from the light side of the balance and divide the marbles from the heavy side of the balance between the two pans. As shown in Figure 12-3, you continue this process until each pan holds only one marble, at which point the heavy marble is the only marble on the heavy side of the balance. Using this process you can always identify the heavy marble in three weighings.

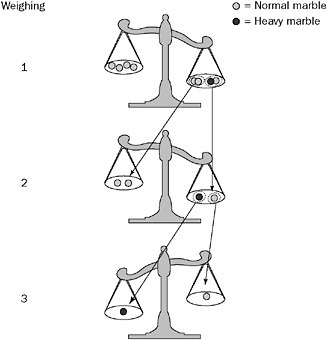
Figure 12-3

This may seem to be the correct answer. The solution wasn’t completely obvious, and it’s an improvement over weighing the marbles one by one. If you’re telling yourself that this seemed too easy, you’re right. The method described so far is a good start, but it’s not the best you can do.

How can you find the heavy marble in fewer than three weighings? Obviously, you’ll have to eliminate more than half the marbles at each weighing, but how can you do that?

Try looking at this problem from an information flow perspective. Information about the marbles comes from the balance, and you use this information to identify the heavy marble. The more information you derive from each weighing, the more efficient your search for the marble will be. Think about how you get information from the balance: You place marbles on it and then look at the result. What are all the possible results? The left pan side could be heavier, the right side could be heavier, or both sides could weigh exactly the same. So there are three possible results, but so far you’ve been using only two of them. In effect, you’re only using 2/3 of the information that each weighing provides. Perhaps if you alter your method so that you use all of the information from each weighing you will be able to find the heavy marble in fewer weighings.

Using the binary search strategy, the heavy marble is always in one of the two pans, so there will always be a heavy side of the balance. In other words, you can’t take advantage of all the information the balance can provide if the heavy marble is always on the balance. What if you divided the marbles into three equal-sized groups, and weighed two of the groups on the balance? Just as before, if either side of the balance is heavier, you know that the heavy marble is in the group on that side. But now it’s also possible that the two groups of marbles on the balance will weigh the same - in this case, the heavy marble must be in the third group that’s not on the balance. Because you divided the marbles into three groups, keeping just the group with the heavy marble eliminates 2/3 of the marbles instead of half of them. This seems promising.

There’s still a minor wrinkle to work out before you can apply this process to the problem at hand. Eight isn’t evenly divisible by three, so you can’t divide the eight marbles into three equal groups. Why do you need the same number of marbles in each group? You need the same number of marbles so that when you put the groups on the balance the result doesn’t have anything to do with differing numbers of marbles on each side. Really, you need only two of the groups to be the same size. You’ll still want all three groups to be approximately the same size so you can eliminate approximately ⅔ of the marbles after each weighing no matter which pile has the heavy marble.

Now you can apply the three-group technique to the problem you were given. Begin by dividing the marbles into two groups of three, which you put on the balance, and one group of two, which you leave off. If the two sides weigh the same, the heavy marble is in the group of two, and you can find it with one more weighing, for a total of two weighings. On the other hand, if either side of the balance is heavier, the heavy marble must be in that group of three. You can eliminate all the other marbles, and place one marble from this group on either side of the balance, leaving the third marble aside. If one side is heavier, it contains the heavy marble; if neither side is heavier, the heavy marble is the one you didn’t place on the balance. This is also a total of two weighings, so you can always find the heavy marble in a group of eight using two weighings. An example of this process is illustrated in Figure 12-4.

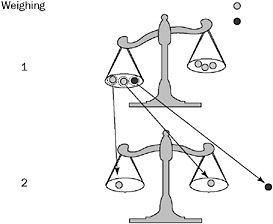
Figure 12-4

Important 

Generalize your solution. What is the minimum number of weighings to find a heavy marble among n marbles?

This is the part where the interviewer determines whether you hit on the preceding solution by luck or because you really understand it. Think about what happens after each weighing. You eliminate 2/3 of the marbles and keep 1/3. After each weighing you have 1/3 as many marbles as you did before. When you get down to one marble, you’ve found the heavy marble.

Based on this reasoning, you can reformulate the question as, “How many times do you have to divide the number of marbles by 3 before you end up with 1?” If you start with 3 marbles, you divide by 3 once to get 1, so it takes one weighing. If you start with 9 marbles you divide by 3 twice, so it takes two weighings. Similarly, 27 marbles require three weighings. What mathematical operation can you use to represent this “How many times do you divide by 3 to get to 1” process?

Because multiplication and division are inverse operations, the number of times you have to divide the number of marbles by 3 before you end up with 1 is the same as the number of times you have to multiply by 3 (starting at 1) before you get to the number of marbles. Repeated multiplication is expressed using exponents. If you want to express multiplying by 3 twice, you can write 3², which is equal to 9. When you multiply twice by 3 you get 9 - it takes two weighings to find the heavy marble among 9 marbles. In more general terms, it takes i weighings to find the heavy marble from among n marbles, where 3ⁱ = n. You know the value of n and want to calculate i, so you need to solve this for i. You can solve for i using logarithms, the inverse operation of exponentiation. If you take log₃ of both sides of the preceding equation you get i = log₃ n.

This works fine as long as n is a power of 3. However, if n isn’t a power of 3, then this equation calculates a noninteger value for i, which doesn’t make much sense, given that it’s extremely difficult to perform a fractional weighing. For example, if n = 8, as in the previous part of the problem, log₃ 8 is some number between 1 and 2 (1.893 … to be a little more precise). From your previous experience, you know it actually takes two weighings when you have eight marbles. This seems to indicate that if you calculate a fractional number of weighings you should round it up to the nearest integer.

Does this make sense? Try applying it to n = 10 and see whether you can justify always rounding up. log₃ 9 is 2, so log₃ 10 will be a little more than two, or three if you round up to the nearest integer. Is that the correct number of weighings for 10 marbles? For 10 marbles, you would start out with two groups of 3 and one group of 4. If the heavy marble were in either of the groups of 3, you could find it with just one more weighing, but if it turned out to be in the group of 4 you might need as many as two more weighings for a total of 3, just as you calculated. In this case the fractional weighing seems to represent a weighing that you might need to make under some circumstances (if the heavy marble happens to be in the larger group) but not others. Because you’re trying to calculate the number of weighings needed to guarantee you’ll find the heavy marble, you have to count that fractional weighing as a full weighing even though you won’t always perform it, so it makes sense to always round up to the nearest integer. In programming, the function that rounds up to the nearest integer is often called ceiling, so you might express the minimum number of weighings needed to guarantee you’ll find the heavy marble among n marbles as ceiling(log₃(n)).

Tip 

For the group of 4 (out of the total of 10 marbles), you would divide the 4 marbles into two groups of 1 and one group of 2. If the heavy marble happened to be in the group of 2, you would need one more weighing (the third weighing) to determine which was the heavy marble. A fractional weighing may also represent a weighing that will always be performed but won’t eliminate a full 2 2/3 of the remaining marbles. For example, when n = 8, the fractional weighing represents the weighing needed to determine which marble is heavier in the case where the heavy marble is known to be in the group of two after the first weighing. In any case, it must be counted as a full weighing, so rounding up is appropriate.

This is another example of a problem designed such that the wrong solution occurs first to most intelligent, logically thinking people. Most people find it quite difficult to come up with the idea of using three groups, but relatively easy to solve the problem after that leap. It’s not an accident that this problem begins by asking you to solve the case of eight marbles. As a power of 2, it works very cleanly for the incorrect solution, but because it’s not a power (or multiple, for that matter) of 3 it’s a little messy for the correct solution. People generally get the correct answer more quickly when asked to solve the problem for nine marbles. Look out for details like this that may steer your thinking in a particular (and often incorrect) direction.

This problem is a relatively easy example of a whole class of tricky problems involving weighing items with a two-pan balance. For more practice with these, you might want to try working out the solution to the preceding problem for a group of marbles in which one marble has a different weight, but you don’t know whether it’s heavier or lighter.