Transforms

Page units are useful for conveniently specifying things and letting the Graphics object sort it out, but there are all kinds of effects that can't be achieved with such a simple transform. A transform is a mathematical function by which units are specified and then transformed into other units. So far, we've talked about transforming from page units to device units, but a more general-purpose transform facility is provided via the Transform property of the Graphics object, which is an instance of the Matrix class:

namespace System.Drawing.Drawing2D {    sealed class Matrix : IDisposable, ... {      // Contructors      public Matrix( ... );      // Properties      public float[] Elements { get; }      public bool IsIdentity { get; }      public bool IsInvertible { get; }      public float OffsetX { get; }      public float OffsetY { get; }      // Methods      public void Invert();      public void Multiply( ... );      public void Reset();      public void Rotate( ... );      public void RotateAt( ... );      public void Scale( ... );      public void Shear( ... );      public void TransformPoints( ... );      public void TransformVectors( ... );      public void Translate( ... );      public void VectorTransformPoints(Point[] pts);    } }

The Matrix class provides an implementation of a 3x3 mathematical matrix, which is a rectangular array of numbers. The specifics of what make up a matrix in math are beyond the scope of this book, but the Matrix class provides all kinds of interesting methods that let you use a matrix without doing any of the math.^[4]

^[4] As with all technology, understanding the underlying principles is always helpful. Martin Heller recommends Introduction to Computer Graphics, by James D. Foley, Andries Van Dam, and Steven K. Feiner (Addison-Wesley, 1993), for the details of matrix math as related to graphics programming.

The graphics transformation matrix is used to transform world coordinates, which is what units involved with graphics operations are really specified in. Graphical units are passed as world coordinates, transformed by the transformation matrix into page units, and finally transformed again from page units to display units. As you've seen, the default page units for the screen are pixels, and that's why no page unit conversion happens without our changing the page unit or the scale or both. Similarly, the default transformation matrix is the identity matrix, which means that it doesn't actually do any conversions.

Scaling

Using an instance of a Matrix object instead of page units, we could perform the simple scaling we did in the preceding example:

// Set units to inches using a transform Matrix matrix = new Matrix(); matrix.Scale(g.DpiX, g.DpiY); g.Transform = matrix; using( Font rulerFont = new Font("MS Sans Serif", 8.25f / g.DpiY) ) using( Pen blackPen = new Pen(Color.Black, 0) ) {   float rulerFontHeight = rulerFont.GetHeight(g); // Inches   // Specify units in inches   RectangleF rulerRect =     new RectangleF(0, 0, 6.5f, rulerFontHeight * 1.5f);   // Draw in inches   g.DrawRectangle(     blackPen,     rulerRect.X,     rulerRect.Y,     rulerRect.Width,     rulerRect.Height);   ... }

This code creates a new instance of the Matrix class, which defaults to the identity matrix.^[5] Instead of directly manipulating the underlying 3x3 matrix numbers, the code uses the Scale method to put the numbers in the right place to scale from inches to pixels using the dpi settings for the current Graphics object. This transformation is exactly the same result that we got by setting the page unit to inches and the page scale to 1, except for one detail: the font. Although the page unit and scale do not affect the size of fonts, the current transform affects everything, including fonts. This is why the point size being passed to the Font's constructor in the sample code is first scaled back by the current dpi setting, causing it to come out right after the transformation has occurred. I'd show you the result of using the transform instead of page units, but because it looks just like Figure 7.1, it'd be pretty boring.

^[5] Also demonstrated is a technique that allows you to tie multiple using statements to the life of a single block, a practice that makes for neater code.

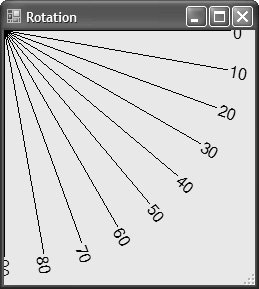
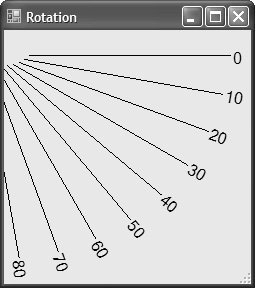
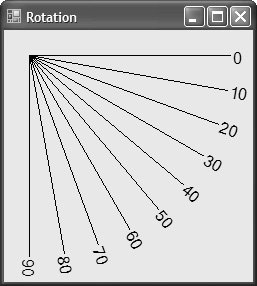
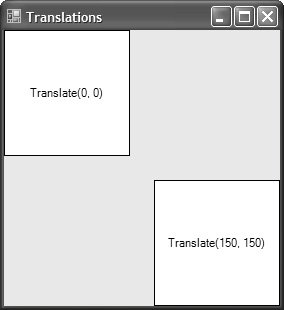
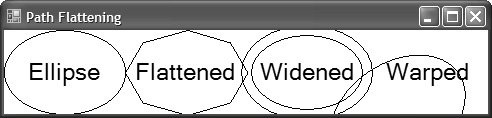
Scaling Fonts

Because the world transform works with fonts as well as everything else, scaling fonts is an interesting use of the world transform all by itself. Usually, fonts are specified by height only, but using transforms allows us to adjust a font's height and width independently of each other, as shown in Figure 7.2.

Figure 7.2. Scaling Font Height Independently of Font Width

Notice that scaling can even be used in the negative direction, as shown on the far right of Figure 7.2, although you must specify the rectangle appropriately:

Matrix matrix = new Matrix(); matrix.Scale(-1, -1); g.Transform = matrix; g.DrawString(   "Scale(-1, -1)",   this.Font,   Brushes.Black,   new RectangleF(-x - width, -y - height, width, height),   ...);

Because scaling by 1 in both dimensions causes all coordinates to be multiplied by 1, we use negative coordinates to get a rectangle at the appropriate place in the window. Notice that the width and height are still positive, however, because a rectangle needs positive dimensions to have positive area.

Rotation

Scaling by a negative amount can look very much like rotation, but only in a limited way. Luckily, matrices support rotation directly, as in this code sample, which draws a line rotated along a number of degrees (see Figure 7.3):

Figure 7.3. Line from (0, 0) to (250, 0) Rotated by Degrees 090

for( int i = 0; i <= 90; i += 10 ) {   Matrix matrix = new Matrix();   matrix.Rotate(i);   g.Transform = matrix;   g.DrawLine(Pens.Black, 0, 0, 250, 0);   g.DrawString(i.ToString(), ... ); }

Notice that rotation takes place starting to the right horizontally and proceeding clockwise. Both shapes and text are rotated, as would anything else drawn into the rotated Graphics object.

Rotate works well if you're rotating around graphical elements with origins at (0, 0), but if you're drawing multiple lines originating at a different origin, the results may prove unintuitive (although mathematically sound), as shown in Figure 7.4.

Figure 7.4. Line from (25, 25) to (275, 25) Rotated by Degrees 090

To rotate more intuitively around a point other than (0, 0), use the RotateAt method (as shown in Figure 7.5):

Figure 7.5. Line from (25, 25) to (275, 25) Rotated by Degrees 090 at (25, 25)

for( int i = 0; i <= 90; i += 10 ) {    Matrix matrix = new Matrix();    matrix.RotateAt(i, new PointF(25, 25));    g.Transform = matrix;    g.DrawLine(Pens.Black, 25, 25, 275, 25);    g.DrawString(      i.ToString(), this.Font, Brushes.Black, textRect, format); }

Translation

Instead of moving our shapes relative to the origin, as we did when drawing the lines, it's often handy to move the origin itself by translating the matrix (as demonstrated in Figure 7.6).

Figure 7.6. Rectangle (0, 0, 125, 125) Drawn at Two Origins

Translation is very handy when you have a figure to draw that can take on several positions around the display area. You can always draw starting from the origin and let the translation decide where the figure actually ends up:

void DrawLabeledRect(Graphics g, string label) {    // Always draw at (0, 0) and let the client    // set the position using a transform    RectangleF rect = new RectangleF(0, 0, 125, 125);    StringFormat format = new StringFormat();    format.Alignment = StringAlignment.Center;    format.LineAlignment = StringAlignment.Center;    g.FillRectangle(Brushes.White, rect);    g.DrawRectangle(Pens.Black, rect.X, rect.Y, rect.Width, rect.Height);    g.DrawString(label, this.Font, Brushes.Black, rect, format); } void TranslationForm_Paint(object sender, PaintEventArgs e) {   Graphics g = e.Graphics;   // Origin at (0, 0)   DrawLabeledRect(g, "Translate(0, 0)");   // Move origin to (150, 150)   Matrix matrix = new Matrix();   matrix.Translate(150, 150);   g.Transform = matrix;   DrawLabeledRect(g, "Translate(150, 150)"); }

In fact, you can use this technique for any of the matrix transformation effects covered so far, in addition to the one yet to be covered: shearing.

Shearing

Shearing is like drawing on a rectangle and then pulling along an edge while holding the opposite edge down. Shearing can happen in both directions independently. A shear of zero represents no shear, and the "pull" is increased as the shear increases. The shear is the proportion of the opposite dimension from one corner to another.

For example, the rectangle (0, 0, 200, 50) sheared 0.5 along the x dimension has its topleft edge at (0, 0) but its bottom-left edge at (25, 50). Because the shear dimension is x, the top edge follows the coordinates of the rectangle, but the bottom edge is offset by the height of the rectangle multiplied by the shear value:

bottomLeftX = height * xShear = 50 * 0.5 = 25

Here's the code that results in the middle sheared rectangle and text in Figure 7.7:

Figure 7.7. Drawing a Constant-Size Rectangle at Various Shearing Values

RectangleF rect = new RectangleF(0, 0, 200, 50); Matrix matrix = new Matrix(); matrix.Shear(.5f, 0f); // Shear in x dimension only matrix.Translate(200, 0); g.Transform = matrix; g.DrawString("Shear(.5, 0)", this.Font, Brushes.Black, rect, format); g.DrawRectangle(Pens.Black, rect.X, rect.Y, rect.Width, rect.Height);

Combining Transforms

In addition to a demonstration of shearing, the preceding code snippet offers another interesting thing to notice: the use of two operationsa translation and a shearon the matrix. Multiple operations on a matrix are cumulative. This is useful because the translation allows you to draw the sheared rectangle in the middle at a translated (0, 0) without stepping on the rectangle at the right (and the rectangle at the right is further translated out of the way of the rectangle in the middle).

It's a common desire to combine effects in a matrix, but be careful, because order matters. In this case, because translation works on coordinates and shear works on sizes, the two operations can come in any order. However, because scaling works on coordinates as well as sizes, the order in which scaling and translation are performed matters very much. For example, this code results in Figure 7.8:

Figure 7.8. Scale Before Translate

Matrix matrix = new Matrix(); matrix.Scale(2, 3); // Scale x/width and y/width by 2 and 3 matrix.Translate(10, 20); // Move origin to (20, 60)

However, swapping the Translate and Scale method calls produces a different result, shown in Figure 7.9:

Figure 7.9. Translate Before Scale

Matrix matrix = new Matrix(); matrix.Translate(10, 20); // Move origin to (10, 20) matrix.Scale(2, 3); // Scale x/width and y/width by 2 and 3

If you'd like to reuse a Matrix object but don't want to undo all the operations you've done so far, you can use the Reset method to set it back to the identity matrix. Similarly, you can check whether it's already the identity matrix:

Matrix matrix = new Matrix(); // Starts as identity matrix.Rotate( ... ); // Touched by inhuman hands if( !matrix.IsIdentity ) matrix.Reset(); // Back to identity

Transformation Helpers

If you've been following along with this section on transformations, you may have been tempted to reach into the Graphics object's Transform property and call Matrix methods directly:

Matrix matrix = new Matrix(); matrix.Shear(.5f, .5f); g.Transform = matrix; // works g.Transform.Shear(.5f, .5f); // compiles, but doesn't work

Although the Transform property returns its Matrix object, it's returning a copy, so performing operations on the copy has no effect on the transformation matrix of the Graphics object. However, instead of creating Matrix objects and setting the Transform property all the time, you can use several helper methods of the Graphics class that affect the transformation matrix directly:

namespace System.Drawing {    sealed class Graphics : IDisposable, ... {      ...      // Transformation methods of the Graphics class      public void ResetTransform();      public void RotateTransform( ... );      public void ScaleTransform( ... );      public void TranslateTransform( ... );    } }

These methods are handy for simplifying transformation code because each call is cumulative (although there's no ShearTransform method):

// No new Matrix object required g.TranslateTransform(200, 0); g.DrawString("(0, 0)", this.Font, Brushes.Black, 0, 0);

Path Transformations

As you've seen in previous chapters, GraphicsPath objects are very similar to Graphics objects, and the similarity extends to transformations. A GraphicsPath object can be transformed just as a Graphics object can, and that's handy when you'd like some parts of a drawing, as specified in paths, to be transformed but not others.

Because a path is a collection of figures to be drawn as a group, a transformation isn't a property to be set and changed; instead, it is an operation that is applied. To transform a GraphicsPath, you use the Transform method:

GraphicsPath CreateLabeledRectPath(string label) {    GraphicsPath path = new GraphicsPath();    // Add rectangle and string    ...    return path; } void PathTranslationForm_Paint(object sender, PaintEventArgs e) { Graphics g = e.Graphics; using( GraphicsPath path = CreateLabeledRectPath("My Path") ) {   // Draw at (0, 0)   g.DrawPath(Pens.Black, path);   // Translate all points in path by (150, 150)   Matrix matrix = new Matrix();   matrix.Translate(150, 150);   path.Transform(matrix);   g.DrawPath(Pens.Black, path); }

In addition, GraphicsPath provides transformations that do flattening, widening, and warping via the Flatten, Widen, and Warp methods, respectively (as shown in Figure 7.10).

Figure 7.10. Path Flattening, Widening, and Warping

Each of these methods takes a Matrix object in case you'd like to, for example, translate and widen at the same time. Passing the identity matrix allows each of the specific operations to happen without an additional transformation. The Flatten method takes a flatness value; the larger the value, the fewer the number of points used along a curve and, therefore, the flatter the curve. Figure 7.10 shows an ellipse flattened by 10:

// Pass the identity matrix as the first argument to // stop any transformation except for the flattening path.Flatten(new Matrix(), 10); g.DrawPath(Pens.Black, path);

The Widen method takes a Pen whose width is used to widen the lines and curves along the path. Figure 7.10 shows an ellipse widened by a pen of width 10:

using( Pen widenPen = new Pen(Color.Empty /* ignored */, 10) ) {   path.Widen(widenPen);   g.DrawPath(Pens.Black, path); }

One of the overloads of the Widen method takes a flatness value, in case you'd like to widen and flatten simultaneously, in addition to the matrix that it also takes for translation.

The Warp method acts like the skewing of an image discussed in Chapter 5. Warp takes, at a minimum, a set of points that defines a parallelogram that describes the target, and a rectangle that describes a chunk of the source. It uses these arguments to skew the source chunk to the destination parallelogram. Figure 7.10 shows the top half of an ellipse skewed left:

// Draw warped PointF[] destPoints = new PointF[3]; destPoints[0] = new PointF(width / 2, 0); destPoints[1] = new PointF(width, height); destPoints[2] = new PointF(0, height / 2); RectangleF srcRect = new RectangleF(0, 0, width, height / 2); path.Warp(destPoints, srcRect); g.DrawPath(Pens.Black, path);