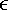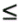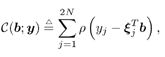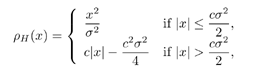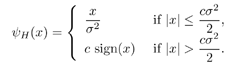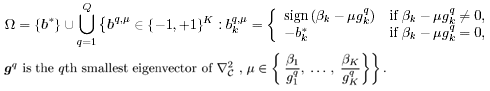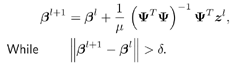4.6 Robust Multiuser Detection Based on Local Likelihood Search

4.6 Robust Multiuser Detection Based on Local Likelihood Search

Recall that in Section 3.4 we introduced a nonlinear multiuser detection method based on local likelihood search, which offers significant performance improvement over linear multiuser detection methods with comparable computational complexity. When combined with the subspace technique, this method also leads to a nonlinear group-blind multiuser detector. In this section we discuss the application of such a local likelihood search method in robust multiuser detection and group -blind robust multiuser detection. The materials in this section were developed in [455, 456].

4.6.1 Exhaustive-Search and Decorrelative Detection

Consider the following complex-valued discrete-time synchronous CDMA signal model . At any time instant, the received signal is the superposition of K users' signals, plus the ambient noise, given by

Equation 4.96

Equation 4.97

where, as before, , c _i,k {+1, -1}, is the normalized signature sequence of the k th user ; N is the processing gain; b _k {+1, -1} and A k are, respectively, the data symbol and the complex amplitude of the k th user; ; and is a complex vector of i.i.d. ambient noise samples with independent real and imaginary components . Denote

where u is a real noise vector consisting of 2 N i.i.d. samples. Then (4.97) can be written as

Equation 4.98

It is assumed that each element u _j of u follows a two- term Gaussian mixture distribution:

Equation 4.99

with 0 < 1 and k > 1. Note that the overall variance of the noise sample u _j is

Equation 4.100

We have Cov ( u ) = ( s ² /2) I _2N and Cov ( n ) = s ² I _N .

Recall from the preceding sections that there are primarily two categories of multiuser detectors for estimating b from y in (4.98), all based on minimizing the sum of a certain function r ( ·) of the chip residuals

Equation 4.101

where denotes the j th row of the matrix Y . These are as follows.

• Exhaustive-search detectors:

  Equation 4.102

  

  
  

• Decorrelative detectors:

  Equation 4.103

  

  
  

  Equation 4.104

  

  
  

Note that exhaustive-search detection is based on the discrete minimization of the cost function C ( b;y ), over 2 ^K candidate points, whereas decorrelative detection is based on the continuous minimization of the same cost function. As before, let y = r ' be the derivative of the penalty function r . In general, the optimization problem (4.103) can be solved iteratively according to the following steps [553]:

Equation 4.105

Equation 4.106

Recall further from Section 4.2 the following three choices of the penalty function r ( ·) in (4.101), corresponding to different forms of detectors:

• Log-likelihood penalty function:

  Equation 4.107

  

  
  

  Equation 4.108

  

  
  

  where f ( ·) denotes the pdf of the noise sample u _j . In this case, the exhaustive-search detector (4.102) corresponds to the ML detector, and the decorrelative detector (4.104) corresponds to the ML decorrelator.

• Least-squares penalty function:

  Equation 4.109

  

  
  

  Equation 4.110

  

  
  

  In this case, the exhaustive-search detector (4.102) corresponds to the ML detector based on a Gaussian noise assumption, and the decorrelative detector (4.104) corresponds to the linear decorrelator.

• Huber penalty function:

  Equation 4.111

  

  
  

  Equation 4.112

  

  
  

  where s ² /2 is the noise variance given by (4.100) and

  Equation 4.113

  

  
  

  is a constant. In this case, the exhaustive-search detector (4.102) corresponds to the discrete minimizer of the Huber cost function, and the decorrelative detector (4.104) corresponds to the robust decorrelator.

4.6.2 Local-Search Detection

Clearly, the optimal performance is achieved by the exhaustive-search detector with the log-likelihood penalty function (i.e., the ML detector). As will be seen later, the performance of the exhaustive-search detector with the Huber penalty function is close to that of the ML detector, while this detector does not require knowledge of the exact noise pdf. However, the computational complexity of the exhaustive-search detector (4.102) is on the order of (2 ^K ). We next discuss a local-search approach to approximating the solution to (4.102), based on the slowest-descent search method discussed in Section 3.4. The basic idea is to minimize the cost function C ( b;y ) over a subset W of the discrete parameter set {+1, -1} ^K that is close to the continuous stationary point b given by (4.103). More precisely, we approximate the solution to (4.102) by a local one:

Equation 4.114

In the slowest-descent-search method, the candidate set W consists of the discrete parameters chosen such that they are in the neighborhood of Q ( Q K ) lines in , which are defined by the stationary point b and the Q eigenvectors of the Hessian matrix of C ( b;y ) at b corresponding to the Q smallest eigenvalues.

For the three types of penalty functions, the Hessian matrix at the stationary points are given, respectively, by

Equation 4.115

Equation 4.116

Equation 4.117

where, in (4.115),

Equation 4.118

and in (4.117) the indicator function I ( y a ) = 1 if y a and 0 otherwise ; hence in this case those rows of Y with large residual signals as a possible result of impulsive noise are nullified, whereas other rows Y of are not affected.

Denote b ^* sign( b ). In general, the slowest-descent-search method chooses the candidate set W in (4.114) as follows:

Equation 4.119

Hence, { b ^{q, m} } m contains the K closest neighbours of b in {-1, +1} ^K along the direction of g ^q Note that { g ^q } represent the Q mutualy orthogonal directions where the cost function C ( b;y ) grows the slowest from the minimum point b .

Finally, we summarize the slowest-descent-search algorithm for robust multiuser detection in non-Gaussian noise. Given a penalty function r ( ·), this algorithm solves the discrete optimization problem (4.114) according to the following steps.

Algorithm 4.4: [Robust multiuser detector based on slowest-descent-search ”synchronous CDMA]

• Compute the continuous stationary point b in (4.103):

  Equation 4.120

  

  
  

  Equation 4.121

  

  
  

  Equation 4.122

  

  
  

  Set and b ^* = sign ( ).

• Compute the Hessian matrix given by (4.115) or (4.116) or (4.117), and its Q smallest eigenvectors g ¹ , . . . , g ^Q .

• Solve the discrete optimization problem defined by (4.114) and (4.119) by an exhaustive search [over (KQ+1) points].

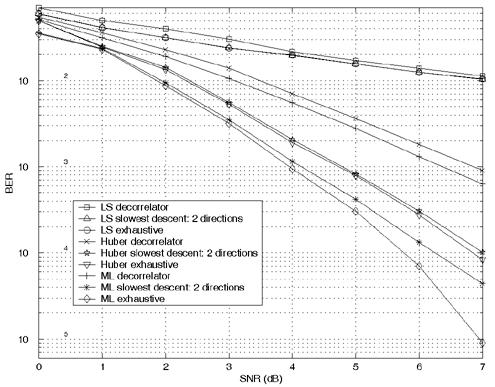
Simulation Results

For simulations, we consider a synchronous CDMA system with a processing gain N = 15, number of users K = 6, and no phase offset and equal amplitudes of user signals (i.e., a _k = 1, k = 1, . . . , K ). The signature sequence s ₁ of user 1 is generated randomly and kept fixed throughout simulations. The signature sequences of other users are generated by circularly shifting the sequence of user 1.

For each of the three penalty functions, Fig. 4.12 presents the BER performance of the decorrelative detector, slowest-descent-search detector with two search directions, and exhaustive-search detector. Searching further slowest-descent directions does not improve the performance in this case. We observe that for all three criteria, the performance of the slowest-descent-search detector is close to that of its respective exhaustive-search version. Moreover, the LS-based detectors have the worst performance. Note that the detector based on the Huber penalty function and the slowest-descent search offers significant performance gain over the robust decorrelator developed in Section 4.4 (Algorithm 4.1). For example, at the BER of 10 ^-3 , it is only less than 1 dB from the ML detector, whereas the robust decorrelator is about 3 dB from the ML detector.

Figure 4.12. BER performance of various detectors in a DS-CDMA system with non-Gaussian ambient noise. N = 15, K = 8 = 0.01, k = 100.