4.3 Asymptotic Performance of Robust Multiuser Detection
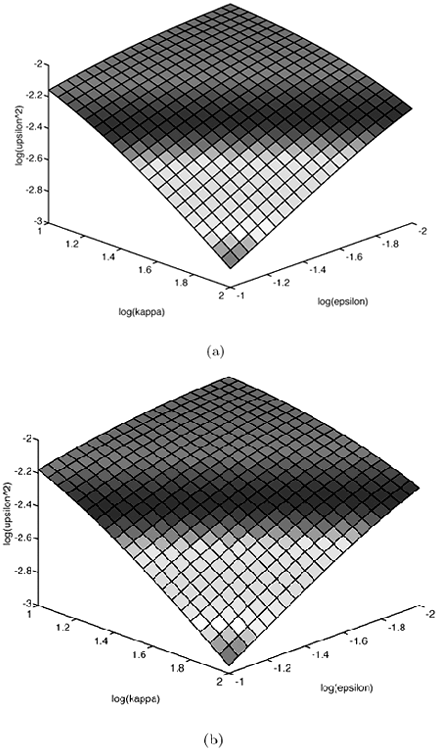
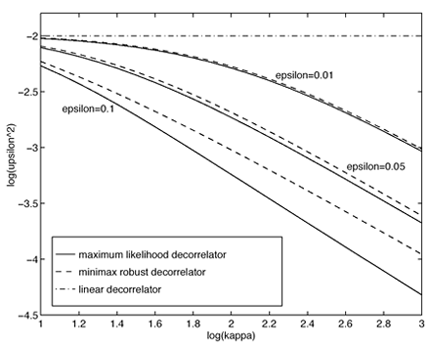
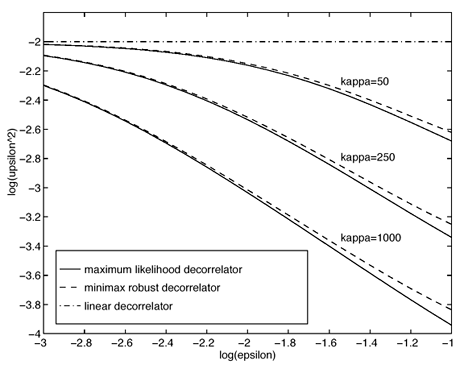
4.3 Asymptotic Performance of Robust Multiuser Detection4.3.1 Influence Function The influence function (IF) introduced by Hampel [170, 203], is an important tool used to study robust estimators. It measures the influence of a vanishingly small contamination of the underlying distribution on the estimator. It is assumed that the estimator can be defined as a functional T , operating on the empirical distribution function of the observation F n , [i.e., T = T ( F n )] and that the estimator is consistent as n Equation 4.31 where D x is the distribution that puts a unit mass at x . Roughly speaking, the influence function IF ( x; T, F ) is the first derivative of the statistic T at an underlying distribution F and at the coordinate x . We next compute the influence function of the nonlinear decorrelating multiuser detectors defined by (4.15). Denote the j th row of the matrix S by Equation 4.32 If G n is the empirical distribution function generated by the signal samples { r j , x j } Equation 4.33 for all distributions G for which the integral is defined. Let the distribution be Equation 4.34 Substituting this distribution into (4.33), differentiating with respect to t , and evaluating the derivative at t = 0, we get Equation 4.35 where by definition, Equation 4.36 Note that by (4.33) the second term on the right-hand side of (4.35) equals zero: Equation 4.37 Now assume that the functional Equation 4.38 where Equation 4.39 is the cross-correlation matrix of the random infinite-length signature waveforms of the K users. From (4.38) we obtain the influence function of the nonlinear decorrelating multiuser detectors determined by (4.15) as Equation 4.40 The influence function above is instrumental to deriving the asymptotic performance of the robust multiuser detectors, as explained below. 4.3.2 Asymptotic Probability of Error Under certain regularity conditions, the M -estimators defined by (4.14) or (4.15) are consistent and asymptotically Gaussian [170]; that is (here we denote Equation 4.41 where the asymptotic covariance matrix is given by Equation 4.42 and where (4.42) follows from (4.32) and (4.40). We can also compute the Fisher information matrix for the parameters q at the underlying noise distribution. Define the likelihood score vector as Equation 4.43 The Fisher information matrix is then given by Equation 4.44 It is known that the maximum likelihood estimate based on i.i.d. samples is asymptotically unbiased and the asymptotic covariance matrix is J ( q ) “1 [377]. As discussed earlier, the maximum likelihood estimate of q corresponds to having y ( x ) = “ f '( x )/ f ( x ). Hence we can deduce that the asymptotic covariance matrix Equation 4.45 where we have assumed that f '( “ Next we consider the asymptotic probability of error for the class of decorrelating detectors defined by (4.15) as the processing gain N Equation 4.46 where u is the asymptotic variance given by Equation 4.47 Hence for the class of M -decorrelators defined by (4.15), their asymptotic probabilities of detection error are determined by the parameter u . We next compute u for the three decorrelating detectors discussed in Section 4.2.3, under the Gaussian mixture noise model (4.3). Linear Decorrelating DetectorThe asymptotic variance for the linear decorrelator is given by Equation 4.48 That is, asymptotically, the performance of the linear decorrelating detector is determined completely by the noise variance, independent of the noise distribution. However, as will be seen later, the noise distribution does affect substantially the finite sample performance of the linear decorrelating detector. Maximum-Likelihood Decorrelating DetectorThe variance of the estimate used in the maximum-likelihood decorrelating detector achieves the Fisher information covariance matrix, and we have Equation 4.49 In fact, (4.49) gives the minimum achievable u 2 . To see this, we use the Cauchy “Schwarz inequality, to yield Equation 4.50 where the last equality follows from the fact that y ( u ) f ( u ) Equation 4.51 Hence it follows from (4.50) that Equation 4.52 Minimax Decorrelating DetectorFor the minimax decorrelating detector, we have Equation 4.53 Equation 4.54 where 1 W ( x ) denotes the indicator function of the set W , and d x denotes the Dirac delta function at x . After some algebra, we obtain Equation 4.55 Equation 4.56 The asymptotic variance In Fig. 4.2 we plot the asymptotic variance u 2 of the maximum-likelihood decorrelator and the minimax robust decorrelator as a function of Figure 4.2. Asymptotic variance u 2 of (a) a minimax robust decorrelating detector, and (b) a maximum-likelihood decorrelating detector, as a function of |
EAN: 2147483647
Pages: 91
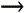
 [i.e.,
[i.e., 

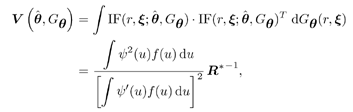
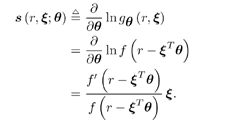
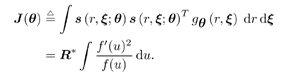

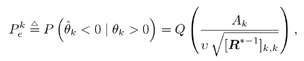
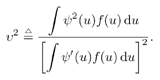
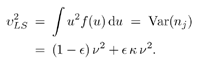
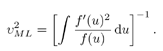

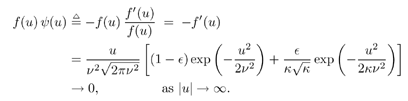

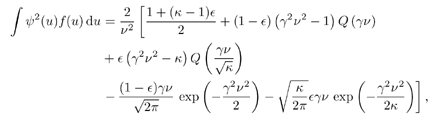
 0.1), while both of the detectors can outperform the linear detector by a substantial margin.
0.1), while both of the detectors can outperform the linear detector by a substantial margin.