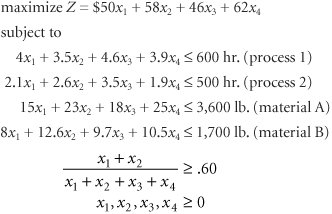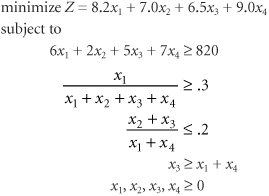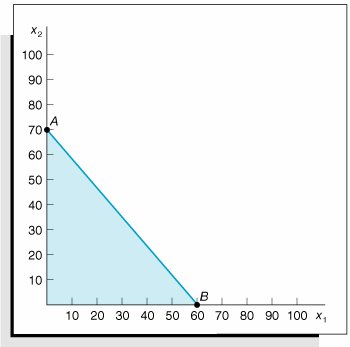
Problems | Introduction to Management Science (10th Edition)

[Page 95]

Given the following QM for Windows computer solution of a linear programming model, graph the problem and identify the solution point, including variable values and slack , from the computer output: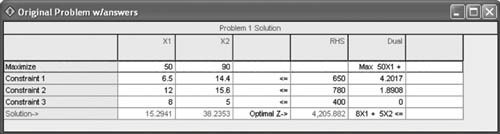

Explain the primary differences between a software package such as QM for Windows and Excel spreadsheets for solving linear programming problems.

Given the following Excel spreadsheet for a linear programming model and Solver window, indicate the formula for cell B13 and fill in the Solver window with the appropriate information to solve the problem:

[Page 96]

Given the following graph of a linear programming model with a single constraint and the objective function maximize Z = 30 x ₁ + 50 x ₂ , determine the optimal solution point:

Determine the values by which c ₁ and c ₂ must decrease or increase in order to change the current solution point to the other extreme point.

Southern Sporting Goods Company makes basketballs and footballs. Each product is produced from two resourcesrubber and leather. The resource requirements for each product and the total resources available are as follows :

	Resource Requirements per Unit
Product	Rubber (lb.)	Leather (ft. ² )
Basketball	3	4
Football	2	5
Total resources available	500 lb.	800 ft. ²

[Page 97]

Each basketball produced results in a profit of $12, and each football earns $16 in profit.

Formulate a linear programming model to determine the number of basketballs and footballs to produce in order to maximize profit.
Transform this model into standard form.

Solve the model formulated in Problem 5 for Southern Sporting Goods Company graphically.

Identify the amount of unused resources (i.e., slack) at each of the graphical extreme points.
What would be the effect on the optimal solution if the profit for a basketball changed from $12 to $13? What would be the effect if the profit for a football changed from $16 to $15?
What would be the effect on the optimal solution if 500 additional pounds of rubber could be obtained? What would be the effect if 500 additional square feet of leather could be obtained?

For the linear programming model for Southern Sporting Goods Company, formulated in Problem 5 and solved graphically in Problem 6:

Determine the sensitivity ranges for the objective function coefficients and constraint quantity values, using graphical analysis.
Verify the sensitivity ranges determined in (a) by using the computer.
Using the computer, determine the shadow prices for the resources and explain their meaning.

A company produces two products, A and B, which have profits of $9 and $7, respectively. Each unit of product must be processed on two assembly lines, where the required production times are as follows.

	Hours/Unit
Product	Line 1	Line 2
A	12	4
B	4	8
Total hours	60	40

Formulate a linear programming model to determine the optimal product mix that will maximize profit.
Transform this model into standard form.

Solve Problem 8 graphically.

Identify the amount of unused resources (i.e., slack) at each of the graphical extreme points.
What would be the effect on the optimal solution if the production time on line 1 were reduced to 40 hours?
What would be the effect on the optimal solution if the profit for product B were increased from $7 to $15? to $20?

10.

For the linear programming model formulated in Problem 8 and solved graphically in Problem 9:

Determine the sensitivity ranges for the objective function coefficients, using graphical analysis.
Verify the sensitivity ranges determined in (a) by using the computer.
Using the computer, determine the shadow prices for additional hours of production time on line 1 and line 2 and indicate whether the company would prefer additional line 1 or line 2 hours.

[Page 98]

11.

Irwin Textile Mills produces two types of cotton clothdenim and corduroy. Corduroy is a heavier grade of cotton cloth and, as such, requires 7.5 pounds of raw cotton per yard, whereas denim requires 5 pounds of raw cotton per yard. A yard of corduroy requires 3.2 hours of processing time; a yard of denim requires 3.0 hours. Although the demand for denim is practically unlimited, the maximum demand for corduroy is 510 yards per month. The manufacturer has 6,500 pounds of cotton and 3,000 hours of processing time available each month. The manufacturer makes a profit of $2.25 per yard of denim and $3.10 per yard of corduroy. The manufacturer wants to know how many yards of each type of cloth to produce to maximize profit.

Formulate a linear programming model for this problem.
Transform this model into standard form.

12.

Solve the model formulated in Problem 11 for Irwin Textile Mills graphically.

How much extra cotton and processing time are left over at the optimal solution? Is the demand for corduroy met?
What is the effect on the optimal solution if the profit per yard of denim is increased from $2.25 to $3.00? What is the effect if the profit per yard of corduroy is increased from $3.10 to $4.00?
What would be the effect on the optimal solution if Irwin Mills could obtain only 6,000 pounds of cotton per month?

13.

Solve the linear programming model formulated in Problem 11 for Irwin Mills by using the computer.

If Irwin Mills can obtain additional cotton or processing time, but not both, which should it select? How much? Explain your answer.
Identify the sensitivity ranges for the objective function coefficients and for the constraint quantity values. Then explain the sensitivity range for the demand for corduroy.

14.

United Aluminum Company of Cincinnati produces three grades (high, medium, and low) of aluminum at two mills. Each mill has a different production capacity (in tons per day) for each grade, as follows:

	Mill
Aluminum Grade	1	2
High	6	2
Medium	2	2
Low	4	10

The company has contracted with a manufacturing firm to supply at least 12 tons of high-grade aluminum, 8 tons of medium-grade aluminum, and 5 tons of low-grade aluminum. It costs United $6,000 per day to operate mill 1 and $7,000 per day to operate mill 2. The company wants to know the number of days to operate each mill in order to meet the contract at the minimum cost.

Formulate a linear programming model for this problem.

15.

Solve the linear programming model formulated in Problem 14 for United Aluminum Company graphically.

How much extra (i.e., surplus ) high-, medium-, and low-grade aluminum does the company produce at the optimal solution?
What would be the effect on the optimal solution if the cost of operating mill 1 increased from $6,000 to $7,500 per day?

[Page 99]
What would be the effect on the optimal solution if the company could supply only 10 tons of high-grade aluminum?

16.

Solve the linear programming model formulated in Problem 14 for United Aluminum Company by using the computer.

Identify and explain the shadow prices for each of the aluminum grade contract requirements.
Identify the sensitivity ranges for the objective function coefficients and the constraint quantity values.
Would the solution values change if the contract requirements for high-grade aluminum were increased from 12 tons to 20 tons? If yes, what would the new solution values be?

17.

The Bradley family owns 410 acres of farmland in North Carolina on which they grow corn and tobacco. Each acre of corn costs $105 to plant, cultivate, and harvest; each acre of tobacco costs $210. The Bradleys have a budget of $52,500 for next year. The government limits the number of acres of tobacco that can be planted to 100. The profit from each acre of corn is $300; the profit from each acre of tobacco is $520. The Bradleys want to know how many acres of each crop to plant in order to maximize their profit.

Formulate a linear programming model for this problem.

18.

Solve the linear programming model formulated in Problem 17 for the Bradley family farm graphically.

How many acres of farmland will not be cultivated at the optimal solution? Do the Bradleys use the entire 100-acre tobacco allotment?
What would the profit for corn have to be for the Bradleys to plant only corn?
If the Bradleys can obtain an additional 100 acres of land, will the number of acres of corn and tobacco they plan to grow change?
If the Bradleys decide not to cultivate a 50-acre section as part of a crop recovery program, how will it affect their crop plans?

19.

Solve the linear programming model formulated in Problem 17 for the Bradley farm by using the computer.

The Bradleys have an opportunity to lease some extra land from a neighbor. The neighbor is offering the land to them for $110 per acre. Should the Bradleys lease the land at that price? What is the maximum price the Bradleys should pay their neighbor for the land, and how much land should they lease at that price?
The Bradleys are considering taking out a loan to increase their budget. For each dollar they borrow , how much additional profit would they make? If they borrowed an additional $1,000, would the number of acres of corn and tobacco they plant change?

20.

The manager of a Burger Doodle franchise wants to determine how many sausage biscuits and ham biscuits to prepare each morning for breakfast customers. The two types of biscuits require the following resources:

Biscuit	Labor (hr.)	Sausage (lb.)	Ham (lb.)	Flour (lb.)
Sausage	0.010	0.10		0.04
Ham	0.024		0.15	0.04

The franchise has 6 hours of labor available each morning. The manager has a contract with a local grocer for 30 pounds of sausage and 30 pounds of ham each morning. The manager also purchases 16 pounds of flour. The profit for a sausage biscuit is $0.60; the profit for a ham biscuit is $0.50. The manager wants to know the number of each type of biscuit to prepare each morning in order to maximize profit.

[Page 100]

Formulate a linear programming model for this problem.

21.

Solve the linear programming model formulated in Problem 20 for the Burger Doodle restaurant graphically.

How much extra sausage and ham is left over at the optimal solution point? Is there any idle labor time?
What would the solution be if the profit for a ham biscuit were increased from $0.50 to $0.60?
What would be the effect on the optimal solution if the manager could obtain 2 more pounds of flour?

22.

Solve the linear programming model developed in Problem 20 for the Burger Doodle restaurant by using the computer.

Identify and explain the shadow prices for each of the resource constraints.
Which of the resources constraints profit the most?
Identify the sensitivity ranges for the profit of a sausage biscuit and the amount of sausage available. Explain these sensitivity ranges.

23.

Rucklehouse Public Relations has been contracted to do a survey following an election primary in New Hampshire. The firm must assign interviewers to conduct the survey by telephone or in person. One person can conduct 80 telephone interviews or 40 personal interviews in a single day. The following criteria have been established by the firm to ensure a representative survey:

At least 3,000 interviews must be conducted .
At least 1,000 interviews must be by telephone.
At least 800 interviews must be personal.

An interviewer conducts only one type of interview each day. The cost is $50 per day for a telephone interviewer and $70 per day for a personal interviewer. The firm wants to know the minimum number of interviewers to hire in order to minimize the total cost of the survey.

Formulate a linear programming model for this problem.

24.

Solve the linear programming model formulated in Problem 23 for Rucklehouse Public Relations graphically.

Determine the sensitivity ranges for the daily cost of a telephone interviewer and the number of personal interviews required.
Does the firm conduct any more telephone and personal interviews than are required, and if so, how many more?
What would be the effect on the optimal solution if the firm were required by the client to increase the number of personal interviews conducted from 800 to a total of 1,200?

25.

Solve the linear programming model formulated in Problem 23 for Rucklehouse Public Relations by using the computer.

If the firm could reduce the minimum interview requirement for either telephone or personal interviews, which should the firm select? How much would a reduction of one interview in the requirement you selected reduce total cost? Solve the model again, using the computer, with the reduction of this one interview in the constraint requirement to verify your answer.
Identify the sensitivity ranges for the cost of a personal interview and the number of total interviews required.

26.

The Bluegrass Distillery produces custom-blended whiskey. A particular blend consists of rye and bourbon whiskey. The company has received an order for a minimum of 400 gallons of the custom blend. The customer specified that the order must contain at least 40% rye and not more than 250 gallons of bourbon. The customer also specified that the blend should be mixed in the ratio of two parts rye to one part bourbon. The distillery can produce 500 gallons per week, regardless of the blend. The production manager wants to complete the order in 1 week. The blend is sold for $5 per gallon.

[Page 101]

The distillery company's cost per gallon is $2 for rye and $1 for bourbon. The company wants to determine the blend mix that will meet customer requirements and maximize profits.

Formulate a linear programming model for this problem.

27.

Solve the linear programming model formulated in Problem 26 for the Bluegrass Distillery graphically.

Indicate the slack and surplus available at the optimal solution point and explain their meanings.
What increase in the objective function coefficients in this model would change the optimal solution point? Explain your answer.

28.

Solve the linear programming model formulated in Problem 26 for the Bluegrass Distillery by using the computer.

Identify the sensitivity ranges for the objective function coefficients and explain what the upper and lower limits are.
How much would it be worth to the distillery to obtain additional production capacity?
If the customer decided to change the blend requirement for its custom-made whiskey to a mix of three parts rye to one part bourbon, how would this change the optimal solution?

29.

Alexis Harrington received an inheritance of $95,000, and she is considering two speculative investmentsthe purchase of land and the purchase of cattle. Each investment would be for 1 year. Under the present (normal) economic conditions, each dollar invested in land will return the principal plus 20% of the principal; each dollar invested in cattle will return the principal plus 30%. However, both investments are relatively risky. If economic conditions were to deteriorate, there is an 18% chance she would lose everything she invested in land and a 30% chance she would lose everything she invested in cattle. Alexis does not want to lose more than $20,000 (on average). She wants to know how much to invest in each alternative to maximize the cash value of the investments at the end of 1 year.

Formulate a linear programming model for this problem.

30.

Solve the linear programming model formulated in Problem 29 for Alexis Harrington graphically.

How much would the return for cattle have to increase in order for Alexis to invest only in cattle?
Should all of Alexis's inheritance be invested according to the optimal solution?
How much "profit" would the optimal solution earn Alexis over and above her investment?

31.

Solve the linear programming model formulated in Problem 29 for Alexis Harrington by using the computer.

If Alexis decided to invest some of her own savings along with the money from her inheritance, what return would she realize for each dollar of her own money that she invested? How much of her own savings could she invest before this return would change?
If the risk of losing the investment in land increased to 30%, how would this change the optimal investment mix?

[Page 102]

32.

Transform the following linear programming model into standard form and solve by using the computer:

33.

Chemco Corporation produces a chemical mixture for a specific customer in 1,000- pound batches. The mixture contains three ingredientszinc, mercury , and potassium. The mixture must conform to formula specifications that are supplied by the customer. The company wants to know the amount of each ingredient it needs to put in the mixture that will meet all the requirements of the mix and minimize total cost.

The customer has supplied the following formula specifications for each batch of mixture:

The mixture must contain at least 200 pounds of mercury.
The mixture must contain at least 300 pounds of zinc.
The mixture must contain at least 100 pounds of potassium.
The ratio of potassium to the other two ingredients cannot exceed 1 to 4.

The cost per pound of mercury is $400; the cost per pound of zinc, $180; and the cost per pound of potassium, $90.

Formulate a linear programming model for this problem.
Solve the model formulated in (a) by using the computer.

34.

The following linear programming model formulation is used for the production of four different products, with two different manufacturing processes and two different material requirements:

Solve this problem by using the computer.
Identify the sensitivity ranges for the objective function coefficients and the constraint quantity values.
Which is the most valuable resource to the firm?
One of the four products is not produced in the optimal solution. How much would the profit for this product have to be for it to be produced?

35.

Island Publishing Company publishes two types of magazines on a monthly basis: a restaurant and entertainment guide and a real estate guide. The company distributes the magazines free to businesses, hotels, and stores on Hilton Head Island in South Carolina. The company's profits come exclusively from the paid advertising in the magazines. Each of the restaurant and entertainment guides distributed generates $0.50 per magazine in advertising revenue, whereas the real estate guide generates $0.75 per magazine. The real estate magazine is a more sophisticated publication that includes color photos, and accordingly it costs $0.25 per magazine to print, compared with only $0.17 for the restaurant and entertainment guide. The publishing company has a printing budget of $4,000 per month. There is enough rack space to distribute at most 18,000 magazines each month. In order to entice businesses to place advertisements, Island Publishing promises to distribute at least 8,000 copies of each magazine. The company wants to determine the number of copies of each magazine it should print each month in order to maximize advertising revenue.

[Page 103]

Formulate a linear programming model for this problem.

36.

Solve the linear programming model formulation in Problem 35 for Island Publishing Company graphically.

Determine the sensitivity range for the advertising revenue generated by the real estate guide.
Does the company spend all of its printing budget? If not, how much slack is left over?
What would be the effect on the optimal solution if the local real estate agents insisted that 12,000 copies of the real estate guide be distributed instead of the current 8,000 copies, or they would withdraw their advertising?

37.

Solve the linear programming model formulated in Problem 35 for Island Publishing Company by using the computer.

How much would it be worth to Island Publishing Company to obtain enough additional rack space to distribute 18,500 copies instead of the current 18,000 copies? 20,000 copies?
How much would it be worth to Island Publishing to reduce the requirement to distribute the entertainment guide from 8,000 to 7,000 copies?

38.

Mega-Mart, a discount store chain, is to build a new store in Rock Springs. The parcel of land the company has purchased is large enough to accommodate a store with 140,000 square feet of floor space. Based on marketing and demographic surveys of the area and historical data from its other stores, Mega-Mart estimates its annual profit per square foot for each of the store's departments to be as shown in the following table:

Department	Profit per ft. ²
Men's clothing	$4.25
Women's clothing	5.10
Children's clothing	4.50
Toys	5.20
Housewares	4.10
Electronics	4.90
Auto supplies	3.80

Each department must have at least 15,000 ft. ² of floor space, and no department can have more than 20% of the total retail floor space. Men's, women's, and children's clothing plus housewares keep all their stock on the retail floor; however, toys, electronics, and auto supplies keep some items (such as bicycles, televisions , and tires) in inventory. Thus, 10% of the total retail floor space devoted to these three departments must be set aside outside the retail area for stocking inventory. Mega-Mart wants to know the floor space that should be devoted to each department in order to maximize profit.

Formulate a linear programming model for this problem.
Solve this model by using the computer.

[Page 104]

39.

In Problem 38 Mega-Mart is considering purchasing a parcel of land adjacent to the current site on which it plans to build its store. The cost of the parcel is $190,000, and it would enable Mega-Mart to increase the size of its store to 160,000 ft. ² Discuss whether Mega-Mart should purchase the land and increase the planned size of the store.
Suppose that the profit per ft. ² will decline in all departments by 20% if the store size increases to 160,000 ft. ² (If the stock does not turn over as fast, increasing inventory costs will reduce profit.) How might this affect Mega-Mart's decision in (a)?

40.

The Food Max grocery store sells three brands of milk in half-gallon cartonsits own brand, a local dairy brand, and a national brand. The profit from its own brand is $0.97 per carton, the profit from the local dairy brand is $0.83 per carton, and the profit from the national brand is $0.69 per carton. The total refrigerated shelf space allotted to half-gallon cartons of milk is 36 square feet per week. A half-gallon carton takes up 16 square inches of shelf space. The store manager knows that each week Food Max always sells more of the national brand than of the local dairy brand and its own brand combined and at least three times as much of the national brand as its own brand. In addition, the local dairy can supply only 10 dozen cartons per week. The store manager wants to know how many half-gallon cartons of each brand to stock each week in order to maximize profit.

Formulate a linear programming model for this problem.
Solve this model by using the computer.

41.

If Food Max in Problem 40 could increase its shelf space for half-gallon cartons of milk, how much would profit increase per carton?
If Food Max could get the local dairy to increase the amount of milk it could supply each week, would it increase profit?
Food Max is considering discounting its own brand in order to increase sales. If it were to do so, it would decrease the profit margin for its own brand to $0.86 per carton, but it would cut the demand for the national brand relative to its own brand in half. Discuss whether the store should implement the price discount.

42.

John Hoke owns Hoke's Spokes, a bicycle shop. Most of John's bicycle sales are customer orders; however, he also stocks bicycles for walk-in customers. He stocks three types of bicyclesroad-racing, cross-country, and mountain. A road-racing bike costs $1,200, a cross-country bike costs $1,700, and a mountain bike costs $900. He sells road-racing bikes for $1,800, cross-country bikes for $2,100, and mountain bikes for $1,200. He has $12,000 available this month to purchase bikes. Each bike must be assembled ; a road-racing bike requires 8 hours to assemble, a cross-country bike requires 12 hours, and a mountain bike requires 16 hours. He estimates that he and his employees have 120 hours available to assemble bikes. He has enough space in his store to order 20 bikes this month. Based on past sales, John wants to stock at least twice as many mountain bikes as the other two combined because mountain bikes sell better.

Formulate a linear programming model for this problem.

43.

Solve the linear programming model formulated in Problem 42 for Hoke's Spokes by using the computer.

Should John Hoke try to increase his budget for purchasing bikes, increase space to stock bikes, or increase labor hours to assemble bikes? Why?
If John were to hire an additional worker for 30 hours at $10 per hour , how much additional profit would he make, if any?
If John were to purchase a cheaper cross-country bike for $1,200 and sell it for $1,900, would this affect the original solution?

44.

Metro Food Services Company delivers fresh sandwiches each morning to vending machines throughout the city. The company makes three kinds of sandwichesham and cheese, bologna, and chicken salad. A ham and cheese sandwich requires a worker 0.45 minutes to assemble, a bologna sandwich requires 0.41 minutes, and a chicken salad sandwich requires 0.50 minutes to make. The company has 960 available minutes each night for sandwich assembly. Vending machine capacity is available for 2,000 sandwiches each day. The profit for a ham and cheese sandwich is $0.35, the profit for a bologna sandwich is $0.42, and the profit for a chicken salad sandwich is $0.37. The company knows from past sales records that its customers buy as many or more of the ham and cheese sandwiches than the other two sandwiches combined, but customers need a variety of sandwiches available, so Metro stocks at least 200 of each. Metro management wants to know how many of each sandwich it should stock to maximize profit.

[Page 105]

Formulate a linear programming model for this problem.

45.

Solve the linear programming problem formulated in Problem 44 for Metro Food Services Company by using the computer.

If Metro Food Services could hire another worker and increase its available assembly time by 480 minutes or increase its vending machine capacity by 100 sandwiches, which should it do? Why? How much additional profit would your decision result in?
What would the effect be on the optimal solution if the requirement that at least 200 sandwiches of each kind be stocked were eliminated? Compare the profit between the optimal solution and this solution. Which solution would you recommend?
What would the effect be on the optimal solution if the profit for a ham and cheese sandwich were increased to $0.40? to $0.45?

46.

Mountain Laurel Vineyards produces three kinds of wineMountain Blanc, Mountain Red, and Mountain Blush. The company has 17 tons of grapes available to produce wine this season . A cask of Blanc requires 0.21 tons of grapes, a cask of Red requires 0.24 tons, and a cask of Blush requires 0.18 tons. The vineyard has enough storage space in its aging room to store 80 casks of wine.

The vineyard has 2,500 hours of production capacity, and it requires 12 hours to produce a cask of Blanc, 14.5 hours to produce a cask of Red, and 16 hours to produce a cask of Blush. From past sales the vineyard knows that demand for the Blush will be no more than half of the sales of the other two wines combined. The profit for a cask of Blanc is $7,500, the profit for a cask of Red is $8,200, and the profit for a cask of Blush is $10,500.

Formulate a linear programming model for this problem.

47.

Solve the linear programming model formulated in Problem 46 for Mountain Laurel Vineyards by using the computer.

If the vineyard were to determine that the profit from Red was $7,600 instead of $8,200, how would that affect the optimal solution?
If the vineyard could secure one additional unit of any of the resources used in the production of wine, which one should it select?
If the vineyard could obtain 0.5 more tons of grapes, 500 more hours of production capacity, or enough storage capacity to store 4 more casks of wine, which should it choose?
All three wines are produced in the optimal solution. How little would the profit for Blanc have to be for it to no longer be produced?

48.

Exeter Mines produces iron ore at four different mines; however, the ores extracted at each mine are different in their iron content. Mine 1 produces magnetite ore, which has a 70% iron content; mine 2 produces limonite ore, which has a 60% iron content; mine 3 produces pyrite ore, which has a 50% iron content; and mine 4 produces taconite ore, which has only a 30% iron content. Exeter has three customers that produce steelArmco, Best, and Corcom. Armco needs 400 tons of pure (100%) iron, Best requires 250 tons of pure iron, and Corcom requires 290 tons. It costs $37 to extract and process 1 ton of magnetite ore at mine 1, $46 to produce 1 ton of limonite ore at mine 2, $50 per ton of pyrite ore at mine 3, and $42 per ton of taconite ore at mine 4. Exeter can extract 350 tons of ore at mine 1; 530 tons at mine 2; 610 tons at mine 3; and 490 tons at mine 4. The company wants to know how much ore to produce at each mine in order to minimize cost and meet its customers' demand for pure (100%) iron.

[Page 106]

Formulate a linear programming model for this problem

49.

Solve the linear programming problem formulated in Problem 48 for Exeter Mines by using the computer.

Do any of the mines have slack capacity? If yes, which one(s)?
If Exeter Mines could increase production capacity at any one of its mines, which should it be? Why?
If Exeter were to decide to increase capacity at the mine identified in (b), how much could it increase capacity before the optimal solution point (i.e., the optimal set of variables ) would change?
If Exeter were to determine that it could increase production capacity at mine 1 from 350 tons to 500 tons, at an increase in production costs to $43 per ton, should it do so?

50.

Given the following linear programming model:

transform the model into standard form and solve by using the computer.

51.

Marie McCoy has committed to the local PTA to make some items for a bake sale on Saturday. She has decided to make some combination of chocolate cakes, loaves of white bread, custard pies, and sugar cookies. Thursday evening she went to the store and purchased 20 pounds of flour, 10 pounds of sugar, and 3 dozen eggs, which are the three main ingredients in all the baked goods she is thinking about making. The following table shows how much of each of the main ingredients is required for each baked good:

	Ingredient
	Flour (cups)	Sugar (cups)	Eggs	Baking Time (min.)
Cake	2.5	2	2	45
Bread	9	0.25		35
Pie	1.3	1	5	50
Cookies	2.5	1	2	16

There are 18.5 cups in a 5 pound bag of flour and 12 cups in a 5 pound bag of sugar. Marie plans to get up and start baking on Friday morning after her kids leave for school and finish before they return after soccer practice (8 hours). She knows that the PTA will sell a chocolate cake for $12, a loaf of bread for $8, a custard pie for $10, and a batch of cookies for $6. Marie wants to decide how many of each type of baked good she should make in order for the PTA to make the most money possible.

[Page 107]

Formulate a linear programming model for this problem.

52.

Solve the linear programming model formulated in Problem 51 for Marie McCoy.

Are any of the ingredients left over?
If Marie could get more of any ingredient, which should it be? Why?
If Marie could get 6 more eggs, 20 more cups of flour, or 30 more minutes of oven time, which should she choose? Why?
The solution values for this problem should logically be integers. If the solution values are not integers, discuss how Marie should decide how many of each item to bake. How do total sales for this integer solution compare with those in the original, non-integer solution?