Appendix Cubic Spline Interpolation
Given a continuous function f on interval [ a, b ] with nodes x i ,i = 0, , n such that a = x < x 1 < · · · < x n = b , a cubic spline interpolant S , is a function such that:
-
The cubic polynomial on the subinterval [ x j ,x j +1 ], j = 0, 1, , n ˆ’ 1 is denoted S ( x ) = S j ( x );
-
S ( x j ) = f ( x j ) for all j = 0, 1, , n ;
-
S j +1 ( x j +1 ) = S j ( x j +1 ) for all j = 0, 1, , n ˆ’ 2;
-
S ² j +1 ( x j +1 ) = S ² j ( x j +1 ) for all j = 0, 1, , n ˆ’ 2;
-
S ³ j +1 ( x j +1 ) = S ³ j ( x j +1 ) for all j = 0, 1, , n ˆ’ 2;
-
Since we have no conclusive information about the second derivative of function f at the boundary nodes, we fit a free or natural cubic spline by imposing the condition:
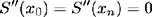
Here, the cubic polynomials take the form:
Applying conditions (1) ˆ’ (5) to the set of polynomials in (A.1.), we arrive at a linear system of equations:
where
and condition (6) gives:
The above equations form a tridiagonal linear system, which may be solved for a unique solution (see [ 13 ]).
EAN: 2147483647
Pages: 132