6.3 Option valuation
6.3 Option valuation
We now examine the equilibrium pricing of a European call option where the underlying is the risk-free zero coupon bond described by (6.7). Without loss of generality, the following assumptions can be made:
-
bond matures as time 1,
-
option expiry is at time where ‰ 1,
-
option exercise price is k ‰ 1.
Further we assume:
-
Markets are frictionless. That is:
-
no transaction costs, no taxes,
-
continuous trading,
-
unlimited lending and borrowing ,
-
unlimited short sales.
-
-
The dynamics of the underlying risk-free zero coupon bond are described by (6.7), which is a non-standard Brownian Bridge process.
-
There exists a risk-free discount bond maturing at time , also described by (6.7). Assume that:

where is the instantaneous correlation between the unexpected returns on bonds maturing at time 1 and respectively. An initial upward sloping yield curve is assumed, that is P (0, ) > P (0, 1), which implies that initial forward rates are positive.
-
Investors are assumed to be rational and to have consensus views on the instantaneous standard deviations of bond returns and their distributions. They need not have the same views of the term structure or expected returns on bonds of various maturities.
By forming a hedge portfolio in bonds and the call, the equilibrium value of a European call may be calculated. The time t price of a European call on a discount bond with maturity 1, expiry and strike k is:
where
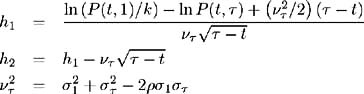
and N ( ·) is the cumulative normal distribution. Here ½ is the volatility, at time of the price of the bond with maturity time 1, i.e. it is the forward bond volatility. Consider the forward bond price P ( , 1) = P ( t, 1)/ P ( t , ). Its volatility may be calculated as:
where ƒ 1 and ƒ are the current (time t ) volatilities of the bonds with maturity time 1 and respectively.
EAN: 2147483647
Pages: 132