6.2 Brownian bridge process
6.2 Brownian bridge process
Let
where { µ ( s ): s ˆˆ [0, 1]} is a Brownian Bridge process and ƒ is the instantaneous standard deviation of the excess return.
{ µ ( s ): s ˆˆ [0, 1]} is a standardised Brownian Bridge process if:
-
P ( µ (0) = 0) = 1,
-
the process is Gaussian, where

and

-
P ( µ (1) = 0) = 1.
Hence the standardised Brownian Bridge process is an augmented standardised Brownian motion [1] with the added requirement that it takes on the value zero at time s = 1. The definition of · ( t, m ) in (6.3) satisfies the requirements that · (0, m )= · ( m, m ) = 0 and hence it may be specified as a Brownian Bridge process.
Our assumption that markets are efficient implies that all currently known information is included in current market prices, or market yields. Under this assumption, the return on the bond can only vary from the deterministic return ¼ ( m ) t , by unanticipated information becoming known. Had this unanticipated information been known, market yields would have adjusted to accommodate it. Hence we may conclude that:
It is appropriate to represent the unexpected returns by means of a Gaussian process, since they are a result of random economic events.
Let { Z ( s ): s ˆˆ [0, ˆ )} be a standardised Brownian motion. The properties of a standardised Brownian motion process, for t 0 and ” 0 where 0 t + ” < 1, imply [2] :
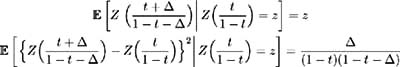
Define a diffusion process W ( t ), as follows :
Hence:
-
P ( W (0) = 0) = 1,
-
P ( W (1) = 0) = 1
-
and
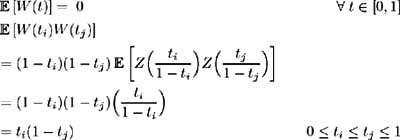
which implies that { W ( t ): t ˆˆ [0, 1]} is a standardised Brownian Bridge process.
If { X ( t ): t ˆˆ T } is a diffusion process, where T is some index set, it may be represented as
where ¼ X ( x, t ) and ƒ X ( x, t ) are respectively, the instantaneous mean and variance of the diffusion process. More specifically , we have:
Hence to determine the process describing the evolution of the Brownian Bridge we need to calculate the instantaneous mean and variance, ¼ W ( w,t ) and ƒ 2 W ( w,t ) respectively. Using the specifications in (6.5) above, we have:

and
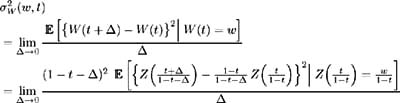
Now:
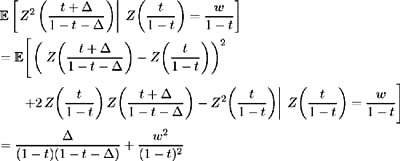
and so:
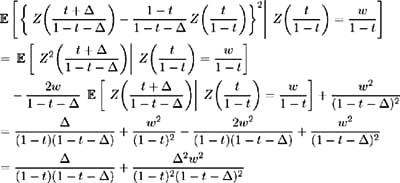
Hence:
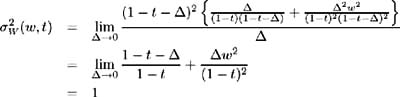
We have determined the instantaneous mean and variance of the standardised Brownian Bridge process to be ![]() and ƒ 2 W ( w,t ) = 1 respectively. Hence the standardised Brownian Bridge process is characterised as:
and ƒ 2 W ( w,t ) = 1 respectively. Hence the standardised Brownian Bridge process is characterised as:
The standardised Brownian Bridge is subject to a restoring force, pulling it back towards zero. The instantaneous variance remains constant, but the total variance, as at time t , is non-stationary and expressed as ![]() [ W 2 ( t )] = t (1 ˆ’ t ). This non-stationarity is due to the imposed terminal constraint. Since the excess return is assumed to have the functional form of (6.3), it is modelled as:
[ W 2 ( t )] = t (1 ˆ’ t ). This non-stationarity is due to the imposed terminal constraint. Since the excess return is assumed to have the functional form of (6.3), it is modelled as:
The economic interpretation of the time t return ¾ ( t, m ), is given by (6.1) and (6.2); hence:

The discount bond price dynamics are determined by application of Ito's Lemma:
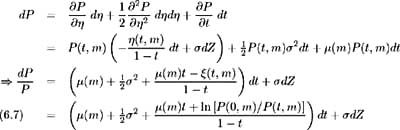
[1] The stochastic process { Z ( s ): s ˆˆ [0, ˆ )} is a standardised Brownian motion if:
-
P ( Z (0) = 0) = 1,
-
the process is Gaussian with

and

[2] Consider a Brownian motion B t starting at x ,thatis P ( B = x ) = 1. Then the following are true [ 43 ]:
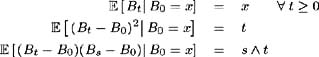
Hence:

and translating this analysis into the required notation, we may calculate
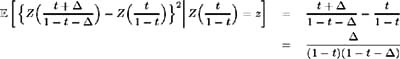
EAN: 2147483647
Pages: 132