CALCULATING A CONFIDENCE INTERVAL

You have spent a lot of time reading about sample means and how they vary. At this stage you may wonder why this is necessary. The reason is very simple. You have to understand these things in order to use statistics for testing hypotheses about the population. If you know how much the means vary from sample to sample, you can draw conclusions about the population by looking at just a single sample. Watch.

Take a well-defined population ” the owners of a particular product X. Suppose that you want to estimate the average satisfaction with that purchase. You randomly select 25 individuals who have returned their registration cards and send them a questionnaire. The average satisfaction response of these 25 customers turns out to be 112, and the standard deviation of their response scores is close to 15, the value for the population. Based on this sample, what can you conclude about all of the customers who have purchased product X?

The sample you selected is one of many possible samples. So the mean you calculated is one of many possible means. In particular, it is one of the means in the distribution of means for samples of size 25. The problem is that you do not know where your sample falls in the distribution of means. Is it close to the true population value? Is it one of the extreme means? Since you do not know the true value for the response of people who have purchased the product, you cannot tell if your sample value is too high, too low, or right on target. You never know the true value in the population, because if you did you would not do the study.

You do not know the population mean, and therefore you do not know the mean of the distribution of sample means. Nevertheless, you can estimate the standard error of the mean from your observed standard deviation. Remember, the standard error of the mean is the standard deviation of the distribution of sample means. The estimated standard error is the standard deviation (15) divided by the square root of the sample size (25), which makes 15 divided by 5, or 3. Using this piece of information, you can visualize the sampling distribution of means, as shown in Figure 4.3.

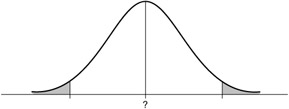
Figure 4.3: The sampling distribution of means.

Based on the Central Limit Theorem, you can assume that the distribution is normal. That is what the Central Limit Theorem says: for a sufficiently large sample size, sample means are normally distributed whether the original variable (safisfaction in this case) is normally distributed or not. Since you do not know the mean satisfaction for the population of owners of the product X, it is labeled with a question mark in the figure. Because the distribution is normal, you know that 95% of all sample means should fall within two standard errors of the mean. The standard error of the mean was found to equal three. So 95% of all sample means should fall within six of the question mark. The values falling outside of this interval are shaded in the figure. (We can do this for any level of standard error.)

Where is your sample mean in this distribution? Sorry ” you cannot figure that out. If you knew the population value (at the question mark), then you could mark the location of the mean; but, of course, you do not. Based on this picture, what can you say about the value of the population mean? Although you cannot give an exact value, you can calculate a range of values ” an interval that should include the population mean 95% of the time. You calculate the lower limit of this interval by subtracting two times the standard error from your mean. The lower limit is therefore 112 - 6 = 106. You calculate the upper limit by adding two times the standard error to your mean. This is 112 + 6 = 118. The interval is from 106 to 118. Now you have what is known as a confidence interval, extending from two standard errors below the sample mean to two standard errors above the sample mean.

Think of what the diagram shows. You can imagine your sample mean somewhere in the distribution and see what happens. Figure 4.4 shows the sample mean at 1.5 standard errors above the population mean (the question mark). The confidence interval is marked off. Does the interval include the unknown population value? Sure ” because it reaches out two standard errors, and the difference between your sample mean and the population mean is only 1.5 standard errors.

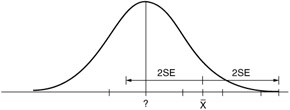
Figure 4.4: The sample mean 1.5 standard errors above the population mean.

Now imagine your sample value at one standard error unit below the mean, as in Figure 4.5. Does the confidence interval still include the population value? Yes. Once again, your sample mean is within two standard errors of the population mean, so the population mean lies within the confidence interval. The only time your interval would not include the population value is when your sample mean falls in the shaded area of Figure 4.3. The shaded region corresponds to the 5% of the distribution that is more than two standard error units from the population mean. (This is the region most often used for analysis. However, in some cases this is not good enough and we have to go out to three even to six standard error units.)

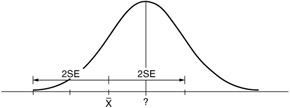
Figure 4.5: The sample mean 1 standard error below the population mean.

You do not know the exact value for the population mean. But as shown here, you can calculate an interval around your sample mean that will include the true, unknown population mean 95% of the time. This is called a 95% confidence interval. Of course, you can never tell whether your particular sample mean is one of the unlikely ones in the shaded region. All you can do is calculate the interval and hope that you have one of the 95-out-of-a-100 times that the interval includes the population value. By the way, there is nothing sacred about the 95% confidence. A given confidence is determined a priori by the experimenter and depends on the practicality of the study. So it is not unusual to see a 90%, 99%, 99.9% or any other confidence.