SUCCESS TESTING
Success testing is a special case of binomial attributes testing for large populations where no failures are allowed. Success testing is the simplest method for demonstrating a required reliability level at a specified confidence level. In this test case, n items are subjected to a test for the specified time of interest, and the specified reliability and confidence levels are demonstrated if no failures occur. The method uses the following relationship:
R = (1 - C) 1/n = ( ² ) 1/n
where R = reliability required; n = number of units tested ; C = confidence level; and ² = consumer's risk.
The necessary sample size to demonstrate the required reliability at a given confidence level is:
n = ![]()
SEQUENTIAL TEST PLAN FOR THE BINOMIAL DISTRIBUTION
The sequential test is a hypothesis testing method in which a decision is made after each sample is tested. When sufficient information is gathered, the testing is discontinued. In this type of testing, sample size is not fixed in advance but depends upon the observations. Sequential tests should not be used when the exact time or cost of the test must be known beforehand or is specified. This type of test plan may be useful when the:
-
Accept/reject criterion for the parts on test is based on attributes
-
Exact test time available and sample size to be used are not known or specified
The test procedure consists of testing parts one at a time and classifying the tested parts as good or defective. After each part is tested, calculations are made based on the test data generated to that point. The decision is made as to whether the test has been passed or failed or if another observation should be made. A sequential test will result in a smaller average number of parts tested when the population tested has a reliability close to either the specified or design reliability. The method to use is described below:
Determine R s , R d , ± . ²
Calculate the accept/reject decision points using:
As each part is tested, classify it as either a failure or success. Evaluate the following expression for the binomial distribution,
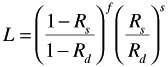
where F = total number of failures and S = total number of successes.
If L > ![]() , the test is failed.
, the test is failed.
If L < ![]() , the test is passed.
, the test is passed.
If ![]() , the test should be continued .
, the test should be continued .
GRAPHICAL SOLUTION
A graphical solution for critical values of f and s is possible by solving the following equations:
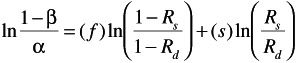
and
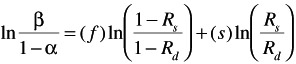
EAN: 2147483647
Pages: 235