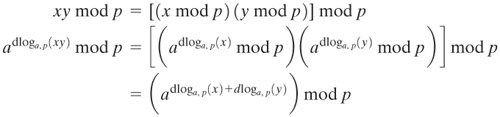Section 8.5. Discrete Logarithms

[Page 247 (continued)]

8.5. Discrete Logarithms

Discrete logarithms are fundamental to a number of public-key algorithms, including Diffie-Hellman key exchange and the digital signature algorithm (DSA). This section provides a brief overview of discrete logarithms. For the interested reader, more detailed developments of this topic can be found in [ORE67] and [LEVE90].

---

[Page 248]

The Powers of an Integer, Modulo n

Recall from Euler's theorem [Equation (8.4)] that, for every a and n that are relatively prime:

af(n) 1(mod where f(n), Euler's totient function, is the number of positive integers less than n and relatively prime to n. Now consider the more general expression:

Equation 8-10

If a and n are relatively prime, then there is at least one integer m that satisfies Equation (8.10), namely, m = f(n). The least positive exponent m for which Equation (8.10) holds is referred to in several ways:

• the order of a (mod n)

• the exponent to which a belongs (mod n)

• the length of the period generated by a

To see this last point, consider the powers of 7, modulo 19:

71		7(mod 19)
72	= 49 = 2 x 19 + 11	11(mod 19)
73	= 343 = 18 x 19 + 1	1(mod 19)
74	= 2401 = 126 x 19 + 7	7(mod 19)
75	= 16807 = 884 x 19 + 11	11(mod 19)

There is no point in continuing because the sequence is repeating. This can be proven by noting that 7³ 1(mod 19) and therefore 7^{3+ 737 7m such that 7m 1(mod 19).}

Table 8.3 shows all the powers of a, modulo 19 for all positive a < 19. The length of the sequence for each base value is indicated by shading. Note the following:

1. All sequences end in 1. This is consistent with the reasoning of the preceding few paragraphs.

2. The length of a sequence divides f(19) = 18. That is, an integral number of sequences occur in each row of the table.

3. Some of the sequences are of length 18. In this case, it is said that the base integer a generates (via powers) the set of nonzero integers modulo 19. Each such integer is called a primitive root of the modulus 19.

---

[Page 249]

Table 8.3. Powers of Integers, Modulo 19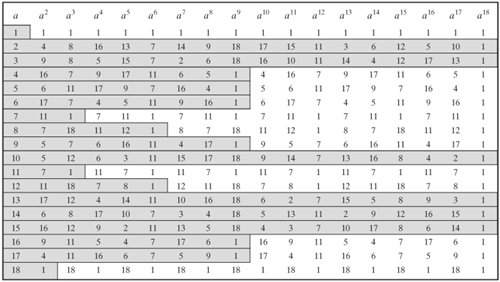

---

[Page 250]

More generally, we can say that the highest possible exponent to which a number can belong (mod n) is f(n). If a number is of this order, it is referred to as a primitive root of n. The importance of this notion is that if a is a primitive root of n, then its powers

a, a²,..., a^f(n)

are distinct (mod n) and are all relatively prime to n. In particular, for a prime number p, if a is a primitive root of p, then

a, a²,..., a^p1

are distinct (mod p). For the prime number 19, its primitive roots are 2, 3, 10, 13, 14, and 15.

Not all integers have primitive roots. In fact, the only integers with primitive roots are those of the form 2, 4, p^a, and 2p^a, where p is any odd prime and a is a positive integer. The proof is not simple but can be found in many number theory books, including [ORE76].

Logarithms for Modular Arithmetic

With ordinary positive real numbers, the logarithm function is the inverse of exponentiation. An analogous function exists for modular arithmetic.

Let us briefly review the properties of ordinary logarithms. The logarithm of a number is defined to be the power to which some positive base (except 1) must be raised in order to equal the number. That is, for base x and for a value y:

y = x^logx(y)

The properties of logarithms include the following:

log_x(1) = 0

log_x(x) = 1

Equation 8-11

Equation 8-12

Consider a primitive root a for some prime number p (the argument can be developed for nonprimes as well). Then we know that the powers of a from 1 through (p 1) produce each integer from 1 through (p 1) exactly once. We also know that any integer b satisfies

b p) for some r, where 0 (by the definition of modular arithmetic. It follows that for any integer b and a primitive root a of prime number p, we can find a unique exponent i such that

b p) where 0 (

---

[Page 251]

This exponent i is referred to as the discrete logarithm of the number b for the base a (mod p). We denote this value as dlog_a.p(b).^[9]

^[9] Many texts refer to the discrete logarithm as the index. There is no generally agreed notation for this concept, much less an agreed name.

Note the following:

Equation 8-13

Equation 8-14

Here is an example using a nonprime modulus, n = 9. Here f(n) = 6 and a = 2 is a primitive root. We compute the various powers of a and find

20 = 1	24 7(mod 9)
21 = 2	25 5(mod 9)
22 = 4	26 1(mod 9)
23 = 8

This gives us the following table of the numbers with given discrete logarithms (mod 9) for the root a = 2:

Logarithm	0	1	2	3	4	5
Number	1	2	4	8	7	5

To make it easy to obtain the discrete logarithms of a given number, we rearrange the table:

Number	1	2	4	5	7	8
Logarithm	0	1	2	5	4	3

Now consider

x	= adloga,p(x) mod p	y = adloga,p(y) mod p
xy	= adloga,p(xy) mod p

Using the rules of modular multiplication,

But now consider Euler's theorem, which states that, for every a and n that are relatively prime:

a^f(n) 1(mod

---

[Page 253]

Any positive integer z can be expressed in the form z = q + kf(n), with 0 f(n). Therefore, by Euler's theorem,

a^z n) if z f(n)

Applying this to the foregoing equality, we have

dlog_a,p(xy) [dlog_{x) + dloga,p(y)] (mod f(p))}

and generalizing,

dlog_a,p(y^r) [a.p(y)] (mod f(n))

This demonstrates the analogy between true logarithms and discrete logarithms.

Keep in mind that unique discrete logarithms mod m to some base a exist only if a is a primitive root of m.

Table 8.4, which is directly derived from Table 8.3, shows the sets of discrete logarithms that can be defined for modulus 19.

Table 8.4. Tables of Discrete Logarithms, Modulo 19 (This item is displayed on page 252 in the print version)

Calculation of Discrete Logarithms

Consider the equation

y = g^x mod p

Given g, x, and p, it is a straightforward matter to calculate y. At the worst, we must perform x repeated multiplications, and algorithms exist for achieving greater efficiency (see Chapter 9).

However, given y, g, and p, it is, in general, very difficult to calculate x (take the discrete logarithm). The difficulty seems to be on the same order of magnitude as that of factoring primes required for RSA. At the time of this writing, the asymptotically fastest known algorithm for taking discrete logarithms modulo a prime number is on the order of [BETH91]:

_e((ln p)^1/3(ln(ln p))^2/3)

which is not feasible for large primes.