[Page 358 (continued)]12.2. Whirlpool[1] [1] Most of the material in this section originally appeared in [STAL O6].
In this section, we examine the hash function Whirlpool [BARR03], one of whose designers is also co-inventor of Rijndael, adopted as the Advanced Encryption Standard (AES). Whirlpool is one of only two hash functions endorsed by NESSIE (New European Schemes for Signatures, Integrity, and Encryption).[2] The NESSIE project is a European Unionsponsored effort to put forward a portfolio of strong cryptographic primitives of various types. [2] The other endorsed scheme consists of three variants of SHA: SHA-256, SHA-384, and SHA-512.
Whirlpool is based on the use of a block cipher for the compression function. As was mentioned in Chapter 11, there has traditionally been little interest in the use of block-cipher-based hash functions because of the demonstrated security vulnerabilities of the structure. The following are potential drawbacks: Block ciphers do not possess the properties of randomizing functions. For example, they are invertible. This lack of randomness may lead to weaknesses that can be exploited. Block ciphers typically exhibit other regularities or weaknesses. For example, [MIYA90] demonstrates how to compromise many hash schemes based on properties of the underlying block cipher. Typically, block-cipher-based hash functions are significantly slower than hash functions based on a compression function specifically designed for the hash function. A principal measure of the strength of a hash function is the length of the hash code in bits. For block-cipher-based hash codes, proposed designs have a hash code length equal to either the cipher block length or twice the cipher block length. Traditionally, cipher block length has been limited to 64 bits (e.g., DES, triple DES), resulting in a hash code of questionable strength.
[Page 359]
However, since the adoption of AES, there has been renewed interested in developing a secure hash function based on a strong block cipher and exhibiting good performance. Whirlpool is a block-cipher-based hash function intended to provide security and performance that is comparable, if not better, than that found in non-block-cipher based hash functions, such as SHA. Whirlpool has the following features: The hash code length is 512 bits, equaling the longest hash code available with SHA. The overall structure of the hash function is one that has been shown to be resistant to the usual attacks on block-cipher-based hash codes. The underlying block cipher is based on AES and is designed to provide for implementation in both software and hardware that is both compact and exhibits good performance.
The design of Whirlpool sets the following security goals: Assume we take as hash result the value of any n-bit substring of the full Whirlpool output. The expected workload of generating a collision is of the order of 2n/2 executions of Whirlpool. Given an n-bit value, the expected workload of finding a message that hashes to that value is of the order of 2n executions of Whirlpool. Given a message and its n-bit hash result, the expected workload of finding a second message that hashes to the same value is of the order of 2n executions of Whirlpool. It is infeasible to detect systematic correlations between any linear combination of input bits and any linear combination of bits of the hash result, or to predict what bits of the hash result will change value when certain input bits are flipped (this means resistance against linear and differential attacks).
The designers assert their confidence that these goals have been met with a considerable safety margin. However, the goals are not susceptible to a formal proof. We begin with a discussion of the structure of the overall hash function, and then examine the block cipher used as the basic building block. Whirlpool Hash Structure Background The general iterated hash structure proposed by Merkle (Figure 11.9) is used in virtually all secure hash functions. However, as was pointed out, there are difficulties in designing a truly secure iterated hash function when the compression function is a block cipher. Preneel [PREN93a, PREN93b] performed a systematic analysis of block-cipher-based hash functions, using the model depicted in Figure 12.5. In this model, the hash code length equals the cipher block length. Additional security problems are introduced and the analysis is more difficult if the hash code length exceeds the cipher block length. Preneel devised 64 possible permutations of the basic model, based on which input served as the encryption key and which served as plaintext and on what input, if any, was combined with the ciphertext to produce the intermediate hash code. Based on his analysis, he concluded that only schemes in which the plaintext was fed forward and combined with the ciphertext were secure. Such an arrangement makes the compression function difficult to invert. [BLAC02] confirmed these results, but pointed out the security problem of using an established block cipher such as AES: The 128-bit hash code value resulting from the use of AES or another scheme with the same block size may be inadequate for security.
[Page 360] Figure 12.5. Model of Single Iteration of Hash Function (hash code equals block length)
Note: Triangular hatch indicates encryption key input. 
Whirlpool Logic Given a message consisting of a sequence of blocks m1, m2,..., mt the Whirlpool hash function is expressed as follows: H0 | = initial value | Hi | = E(Hi-1, mi)  i-1 i-1  i = intermediate value i = intermediate value | Ht | = hash code value |
In terms of the model of Figure 12.5, the encryption key input for each iteration is the intermediate hash value from the previous iteration; the plaintext is the current message block; and the feedforward value is the bitwise XOR of the current message block and the intermediate hash value from the previous iteration. The algorithm takes as input a message with a maximum length of less than 2256 bits and produces as output a 512-bit message digest. The input is processed in 512-bit blocks. Figure 12.6 depicts the overall processing of a message to produce a digest. This follows the general structure depicted in Figure 11.9. The processing consists of the following steps: - Step 1: Append padding bits. The message is padded so that its length in bits is an odd multiple of 256. Padding is always added, even if the message is already of the desired length. For example, if the message is 256 x 3 = 768 bits long, it is padded by 512 bits to a length of 256 x 5 = 1280 bits. Thus, the number of padding bits is in the range of 1 to 512.
Figure 12.6. Message Digest Generation Using Whirlpool (This item is displayed on page 361 in the print version)
Note: Triangular hatch marks key input. 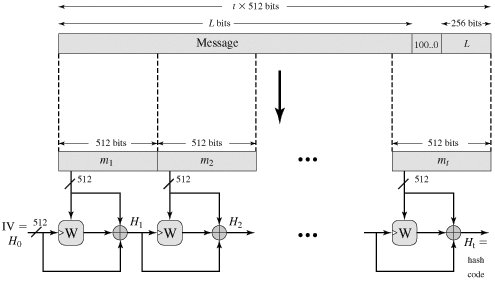
The padding consists of a single 1-bit followed by the necessary number of 0-bits.
[Page 361]- Step 2: Append length. A block of 256 bits is appended to the message. This block is treated as an unsigned 256-bit integer (most significant byte first) and contains the length in bits of the original message (before the padding).
The outcome of the first two steps yields a message that is an integer multiple of 512 bits in length. In Figure 12.6, the expanded message is represented as the sequence of 512-bit blocks m1, m2,..., mt so that the total length of the expanded message is t x 512 bits. These blocks are viewed externally as arrays of bytes by sequentially grouping the bits in 8-bit chunks. However, internally, the hash state Hi is viewed as an 8 x 8 matrix of bytes. The transformation between the two is explained subsequently.
- Step 3: Initialize hash matrix. An 8 x 8 matrix of bytes is used to hold intermediate and final results of the hash function. The matrix is initialized as consisting of all 0-bits.
- Step 4: Process message in 512-bit (64-byte) blocks. The heart of the algorithm is the block cipher W.
Block Cipher W Unlike virtually all other proposals for a block-cipher-based hash function, Whirlpool uses a block cipher that is specifically designed for use in the hash function and that is unlikely ever to be used as a standalone encryption function. The reason for this is that the designers wanted to make use of a block cipher with the security and efficiency of AES but with a hash length that provided a potential security equal to SHA-512. The result is the block cipher W, which has a similar structure and uses the same elementary functions as AES, but which uses a block size and a key size of 512 bits. Table 12.2 compares AES and W.
[Page 362] Although W is similar to AES, it is not simply an extension. Recall that the Rijndael proposal for AES defined a cipher in which the block length and the key length can be independently specified to be 128, 192, or 256 bits. The AES specification uses the same three key size alternatives but limits the block length to 128 bits. AES operates on a state of 4 x 4 bytes. Rijndael with block length 192 bits operates on a state of 4 x 6 bytes. Rijndael with block length 256 bits operates on a state of 4 x 8 bytes. W operates on a state of 8 x 8 bytes. The more the state representation differs from a square, the slower the diffusion goes and the more rounds the cipher needs. For a block length of 512 bits, the Whirlpool developers could have defined a Rijndael operating on a state of 4 x 16 bytes, but that cipher would have needed many rounds and it would have been very slow. As Table 12.2 indicates, W uses a row-oriented matrix whereas AES uses a column-oriented matrix. There is no technical reason to prefer one orientation over another, because one can easily construct an equivalent description of the same cipher, exchanging rows with columns. Table 12.2. Comparison of Whirlpool Block Cipher W and AES| | W | AES |
|---|
Block size (bits) | 512 | 128 | Key size (bits) | 512 | 128, 192, or 256 | Matrix orientation | Input is mapped row-wise | Input is mapped column-wise | Number of rounds | 10 | 10, 12, or 14 | Key expansion | W round function | Dedicated expansion algorithm | GF(28) polynomial | x8 + x4 + x3 + x2 + 1 (011D) | x8 + x4 + x3 + x + 1 (011B) | Origin of S-box | Recursive structure | Multiplicative inverse in GF(28) plus affine transformation | Origin of round constants | Successive entries of the S-box | Elements 2i of GF(28) | Diffusion layer | Right multiplication by 8 x 8 circulant MDS matrix (1, 1, 4, 1, 8, 5, 2, 9) - mix rows | Left multiplication by 4 x 4 circulant MDS matrix (2, 3, 1, 1) - mix columns | Permutation | Shift columns | Shift rows |
Overall Structure Figure 12.7 shows the overall structure of W. The encryption algorithm takes a 512-bit block of plaintext and a 512-bit key as input and produces a 512-bit block of ciphertext as output. The encryption algorithm involves the use of four different functions, or transformations: add key (AK), substitute bytes (SB), shift columns (SC), and mix rows (MR), whose operations are explained subsequently. W consists of a single application of AK followed by 10 rounds that involve all four functions. We can concisely express the operation of a round r as a round function RF that is a composition of functions: Equation 12-1 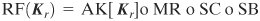
[Page 363]where Kr is the round key matrix for round r. The overall algorithm, with key input K, can be defined as follows: 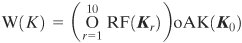
where the large circle indicates iteration of the composition function with index r running from 1 through 10. Figure 12.7. Whirlpool Cipher W 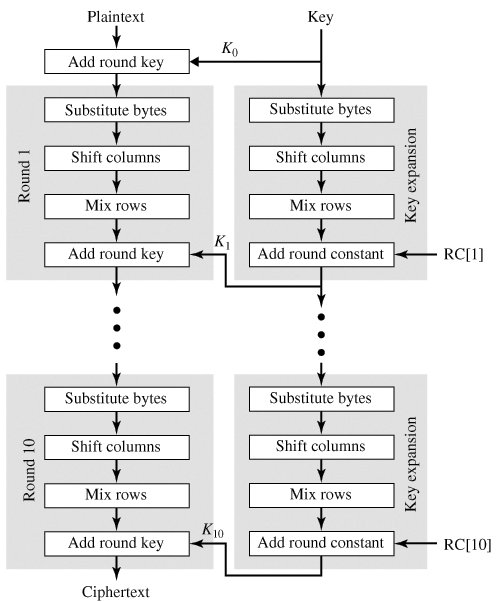
The plaintext input to W is a single 512-bit block. This block is treated as an 8 x 8 square matrix of bytes, labeled CState. Figure 12.8 illustrates that the ordering of bytes within a matrix is by row. So, for example, the first eight bytes of a 512-bit plaintext input to the encryption cipher occupy the first row of the internal matrix CState, the second eight bytes occupy the second row, and so on. The representation of the linear byte stream as a square matrix can be concisely expressed as a mapping function m For a linear byte array X with elements xk(0 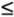 63), the corresponding matrix ai,j(0 63), the corresponding matrix ai,j(0  7)we have the following correspondence: 7)we have the following correspondence: A = m(X)  i,j = x8i + j i,j = x8i + j Figure 12.8. Whirlpool Matrix Structure (This item is displayed on page 364 in the print version) 
Similarly, the 512-bit key is depicted as a square matrix KState of bytes. This key is used as input to the initial AK function. The key is also expanded into a set of 10 round keys, as explained subsequently. We now look at the individual functions that are part of W.
[Page 364]The Nonlinear Layer SB The substitute byte function (SB) is a simple table lookup that provides a nonlinear mapping. W defines a 16 x 16 matrix of byte values, called an S-box (Table 12.3), that contains a permutation of all possible 256 8-bit values. Each individual byte of CState is mapped into a new byte in the following way: The leftmost 4 bits of the byte are used as a row value and the rightmost 4 bits are used as a column value. These row and column values serve as indexes into the S-box to select a unique 8-bit output value. For example, the hexadecimal value[3] {95}references row 9, column 5 of the S-box, which contains the value {BA}. Accordingly, the value {95}is mapped into the value {BA}. The SB function can be expressed by the following correspondence, for an input matrix A and an output matrix B: [3] As we did for AES, a hexadecimal number is indicated by enclosing it in curly brackets when this is needed for clarity.
B = SB(A)  ai,j], 0 ai,j], 0  7 7 where S[x] refers to the mapping of input byte x into output byte S[x] by the S-box. Table 12.3. Whirlpool S-Box (This item is displayed on page 365 in the print version) 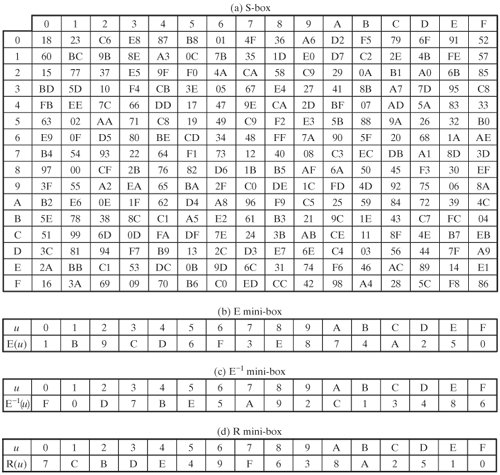
The S-box can be generated by the structure of Figure 12.9. It consists of two nonlinear layers, each containing two 4 x 4 S-boxes separated by a 4 x 4 randomly generated box. Each of the boxes maps a 4-bit input into a 4-bit output. The E box is defined as E(u) = {B}u if u 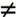 {F} and E({F}) = 0, where arithmetic is performed over the finite field GF(24)with the irreducible polynomial f(x4 + x + 1. {F} and E({F}) = 0, where arithmetic is performed over the finite field GF(24)with the irreducible polynomial f(x4 + x + 1. Figure 12.9. Implementation of Whirlpool S-Box (This item is displayed on page 366 in the print version) 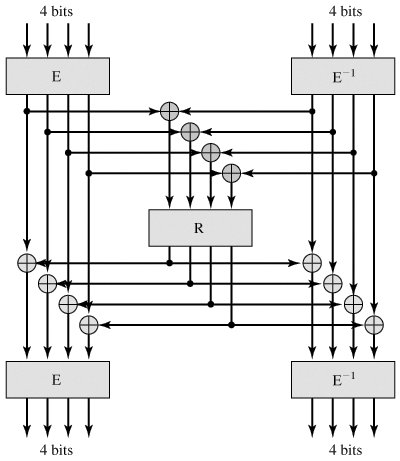
The SB function is designed to introduce nonlinearity into the algorithm. This means that the SB function should exhibit no correlations between linear combinations of a input bits and linear combinations of a output bits. In addition, differences between sets of input bits should not propagate into similar differences among the corresponding output bits; put another way, small input changes should cause large output changes. These two properties help to make W resistant against linear and differential cryptanalysis. The Permutation Layer SC The permutation layer (shift columns) causes a circular downward shift of each column of CState except the first column. For the second column, a 1-byte circular downward shift is performed; for the third column, a 2-byte circular downward shift is performed; and so on. The SC function can be expressed by the following correspondence, for an input matrix A and an output matrix B:
[Page 365] B = SC(A)  a(i - j) mod 8, j 0 a(i - j) mod 8, j 0  i, j i, j  7 7 The shift column transformation is more substantial than it may first appear. This is because CState is treated as an array of eight 8-byte rows. Thus, on encryption, the first 8 bytes of the plaintext are copied to the first row of CState, and so on. A column shift moves an individual byte from one row to another, which is a linear distance of a multiple of 8 bytes. Also note that the transformation ensures that the 8 bytes of one row are spread out to eight different rows. The Diffusion Layer MR Recall from Chapter 3 that for a function that exhibits diffusion, the statistical structure of the input is dissipated into long-range statistics of the output. This is achieved by having each input bit affect the value of many output bits; generally, this results in each output bit being affected by many input bits. The diffusion layer (mix rows) achieves diffusion within each row individually. Each byte of a row is mapped into a new value that is a function of all eight bytes in that row. The transformation can be defined by the matrix multiplication: B = AC where A is the input matrix, B is the output matrix, and C is the transformation matrix:
[Page 366]  Each element in the product matrix is the sum of products of elements of one row and one column. In this case, the individual additions and multiplications[4] are performed in GF(28)with the irreducible polynomial f(x) = x8 + x4 + x3 + x2 + 1. As an example of the matrix multiplication involved, the first element of the output matrix is [4] As we did for AES, we use the symbol · to indicate multiplication over the finite field GF(28)and  to indicate bitwise XOR, which corresponds to addition in GF(28) to indicate bitwise XOR, which corresponds to addition in GF(28)
b0,0 = a0,0  (9 · (2· (5· (8· (4· (9 · (2· (5· (8· (4·
[Page 367]Note that each row of C is constructed by means of a circular right shift of the preceding row. C is designed to be a maximum distance separable (MDS) matrix. In the field of error-correcting codes, an MDS code takes as input a fixed-length bit string and produces an expanded output string such that there is the maximum Hamming distance between pairs of output strings. With an MDS code, even multiple bit errors result in a code that is closer to the correct value than to some other value. In the context of block ciphers, a transformation matrix constructed using an MDS code provides a high degree of diffusion [JUNO04]. The use of MDS codes to provide high diffusion was first proposed in [RIJM96]. The matrix C is an MDS matrix that has as many 1-elements as possible (3 per row). Overall, the coefficients in C provide for efficient hardware implementation. The Add Key Layer AK In the add key layer, the 512 bits of CState are bitwise XORed with the 512 bits of the round key. The AK function can be expressed by the following correspondence, for an input matrix A, an output matrix B, and a round key Ki: B = AK[Ki](A)  ai,j, ai,j,  7 7 Key Expansion for the Block Cipher W As shown in Figure 12.7, key expansion is achieved by using the block cipher itself, with a round constant serving as the round key for the expansion. The round constant for round r(1  10)is a matrix r] in which only the first row is nonzero, and is defined as follows: 10)is a matrix r] in which only the first row is nonzero, and is defined as follows: rc[r]0,j = S[8(r-1)+j], | 0 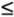 7,1 7,1  10 10 | rc[r]i,j = 0, | 1 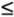 7,0 7,0  7,1 7,1  10 10 |
Each element of the first row is a mapping using the S-box. Thus, the first row of RC[1] is  Using the round constants, the key schedule expands the 512-bit cipher key K onto a sequence of round keys K0, K1, . . ., K10: K0 = K Kr = RF[RC[r]](Kr-1) where RF is the round function defined in Equation (12.1). Note that for the AK phase of each round, only the first row of KState is altered. Performance of Whirlpool As yet, there has been little implementation experience with Whirlpool. Recall that the NIST evaluation of Rijndael determined that it exhibited good performance in both hardware and software and that it is well suited to restricted-space (low memory) requirements. These criteria were important in the selection of Rijndael for AES. Because Whirlpool uses the same functional building blocks as AES and has the same structure, we can expect similar performance and space characteristics.
[Page 368]One study that has been done is reported in [KITS04]. The authors compared Whirlpool with a number of other secure hash functions, including all of the versions of SHA. The authors developed multiple hardware implementations of each hash function and concluded that, compared to SHA-512, Whirlpool requires more hardware resources but performs much better in terms of throughput. |





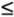



 {F} and E({F}) = 0, where arithmetic is performed over the finite field GF(24)with the irreducible polynomial f(
{F} and E({F}) = 0, where arithmetic is performed over the finite field GF(24)with the irreducible polynomial f(
 i, j
i, j 
 to indicate bitwise XOR, which corresponds to addition in GF(28)
to indicate bitwise XOR, which corresponds to addition in GF(28)