| At this point, we have covered the fundamentals that make a logic engine work. If you understand structures, variables , facts, rules, and programs, you can create query or logic languages that use the engine these objects create. In practice, you may want several additional features, including -
Comparisons -
Arithmetic -
Evaluation -
Not -
Anonymous variables -
Lists 12.9.1 Comparisons A Comparison object compares the values of two terms. These terms can be either variables or structures, but if they are structures, they must be atoms . This restriction follows from the fact that there is no conventional way to compare two structures, such as city(denver, 5280) city(richmond, 19) If you compare these facts by an alphabetic ordering of city name , you will find richmond > denver . If you compare them by altitude, you will find denver > richmond . To ensure that comparisons apply only to atoms, the package sjm.engine has an Atom class. Class Atom , a subclass of Fact , allows no terms. The engine can compare 5280 and 19 , or denver and richmond , but not city(denver, 5280) and city(richmond, 19) . The Comparison class applies the standard Java meaning to these comparison operators: > < >= <= != The Comparison class differs from Java in requiring the operator " = " to effect the results of the Java operator " == ". Figure 12.5 shows the Comparison class. Figure 12.5. The relationship of Comparison and Atom . The terms of a Comparison object must be implementations of ComparisonTerm , specifically Atom objects or Variable objects. 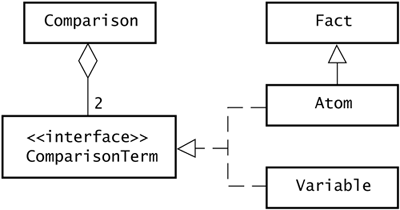 A comparison can function without reference to a program. Here's an example: package sjm.examples.engine; import sjm.engine.*; /** * Show a couple of comparisons. */ public class ShowComparison { public static void main(String[] args) { Atom alt1 = new Atom(new Integer(5280)); Atom alt2 = new Atom(new Integer(19)); Query q1 = new Query( null, // no axiom source new Comparison(">", alt1, alt2)); System.out.println(q1 + " : " + q1.canFindNextProof()); Query q2 = new Query( null, new Comparison(">", new Atom("denver"), new Atom("richmond"))); System.out.println(q2 + " : " + q2.canFindNextProof()); } } This prints the comparisons of 5280 > 19 and "denver" > "richmond" : >(5280, 19) : true >(denver, richmond) : false The second comparison is false because the Comparison class relies internally on the compareTo() method of the String class. This method compares the Unicode values of characters . The Unicode value of d is less than the Unicode value of r , so "denver" is less than "richmond" . Both queries in this program specify null as the axiom source because these queries need no access to a logic program to prove their results. 12.9.2 Arithmetic It is useful for a logic engine to provide a mechanism for representing arithmetic expressions, such as the amount of tax on a coffee order. Figure 12.6 shows the composition of arithmetic operators. Figure 12.6. The ArithmeticOperator class. An ArithmeticOperator object has two arithmetic terms, which may be variables, number facts, or other arithmetic operators. 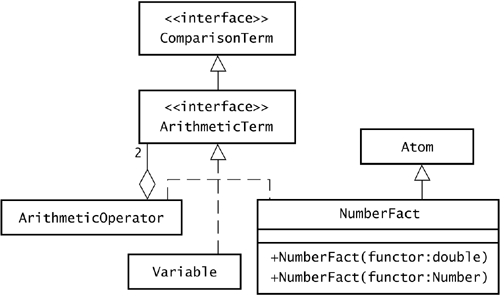 The NumberFact class simplifies the creation of atoms that are numbers . Without NumberFact , creating a structure that holds the number two requires a statement such as Atom two = new Atom(new Integer(2)); With the NumberFact class, an equivalent but shorter statement is NumberFact two = new NumberFact(2); Such simplifications have a limited return. Ultimately, you want to create new languages that replace both statements with simply the character 2 . No amount of refactoring, simplified constructors, or new subclasses will match the power of creating a parser to feed the engine. An ArithmeticOperator object always has two terms, both of which must be implementations of ArithmeticTerm . Three classes in the engine implement ArithmeticTerm : NumberFact , Variable , and ArithmeticOperator . An arithmetic operator can contain other arithmetic operators, and that makes it possible to compose any arithmetic expression. Here is an example: package sjm.examples.engine; import sjm.engine.*; /** * Show how to perform arithmetic within the engine. */ public class ShowArithmetic { public static void main(String[] args) { NumberFact a, b; a = new NumberFact(1000); b = new NumberFact(999); ArithmeticOperator x, y; x = new ArithmeticOperator('*', a, b); y = new ArithmeticOperator('+', x, b); System.out.println(y); System.out.println(y.eval()); } } This program uses the eval() method, which is part of the Term interface. This method returns the value of the Term that the engine will use in arithmetic expressions and comparison functions. Running this program prints the following: +(*(1000.0, 999.0), 999.0) 999999.0 12.9.3 Evaluation An Evaluation object unifies one term with the value of another. This capability is most useful when combined with arithmetic. For example, you might want to evaluate the weight of a baby by weighing yourself holding the baby and then subtracting your own weight. An evaluation displays itself using a pound sign (" # ") as its functor, so an evaluation that computes the weight of a baby might look like this: #(Baby, -(YouAndBaby, You)) Here is a program that shows this evaluation in action: package sjm.examples.engine; import sjm.engine.*; /** * Show an evaluation. */ public class ShowEvaluation { public static void main(String[] args) { Variable you = new Variable("You"); Variable youAndBaby = new Variable("YouAndBaby"); Variable baby = new Variable("Baby"); ArithmeticOperator diff; diff = new ArithmeticOperator('-', youAndBaby, you); Evaluation e = new Evaluation(baby, diff); System.out.println("Before weighing:"); System.out.println(e); you.unify(new NumberFact(185)); youAndBaby.unify(new NumberFact(199)); System.out.println("\nAfter weighing:"); System.out.println(e); e.canFindNextProof(); System.out.println( "\nThat baby weighs about " + baby + " pounds."); } } This program creates three variables, an arithmetic operation, and an evaluation that ties them together. To force the evaluation to execute, the program asks the evaluation to prove itself. The results are Before weighing: #(Baby, -(YouAndBaby, You)) After weighing: #(Baby, -(199.0, 185.0)) That baby weighs about 14.0 pounds. 12.9.4 Not It can be useful to determine that the engine cannot prove a structure. A Not object is a structure that fails if it can prove itself against a program, and succeeds if it cannot prove itself. The Not class has the same constructors as the Structure class, but it proves itself differently. For an example of how a Not object behaves in a logic program, see Section 13.8.3, "Negation," in Chapter 13, "Logic Programming." 12.9.5 Anonymous Variables An anonymous variable unifies successfully with any other term without binding to the term. This is useful for screening out unwanted terms. See Chapter 13 for an example of anonymous variables in action. In sjm.engine , class Anonymous is a subclass of Variable , as Figure 12.7 shows. Anonymous variables print themselves as an underscore (" _ "). Figure 12.7. The Anonymous class. Anonymous variables unify successfully without binding to a value.  12.9.6 Lists A list is a structure that contains a list of terms. Objects of class List can represent sequences of any length, but internally lists always have two terms. The first term of a list can be any term, and the second term of a list is another list. This definition suffices to define a sequence of terms. For example, a list that represents ten items actually contains only two terms. The first term of a ten-item list contains the first item, and the second term contains a nine-item list. The engine manages lists this way because it minimizes the extent to which lists are a special case. The functor of a list is always " . ". Because lists are structures, they need a functor, although in practice you will be more interested in the terms of a list than its functor. You could use any standard value as the functor for lists, and " . " is conventional. The recursive definition of lists requires a termination mechanism, and that is a special object: the empty list. The empty list displays itself as " [] ". For example, a list that contains cobra , garter , and python stores itself internally as .(cobra, .(garter, .(python, []))) . Note that this list contains only two terms: the cobra term and a list of two other snakes . The inner, two-snake list contains garter and a one-snake list. The one-snake list contains python and the empty list. Every list except the empty list contains two terms. The toString() method of class Structure treats lists as a special case so that lists print themselves in a manner that makes them more readable. The list that internally is .(cobra, .(garter, .(python, []))) displays itself as [cobra, garter, python] The power of lists is one of the greatest advantages of logic languages over simple query languages. Chapter 13, "Logic Programming," gives many examples of the use of lists. |