6. Semantic Characterization

While the results above indicate that shot activity is sufficient for purposes of temporal segmentation, the extraction of full-blown semantic descriptions requires a more sophisticated characterization of the elements of mise-en-scene. In principle, it is possible to train a classifier for each semantic attribute of interest, but such an approach is unlikely to scale as the set of attributes grows. An alternative, which we adopt, is to rely on an intermediate representation, consisting of a limited set of sensors tuned to visual attributes that are likely to be semantically relevant, and a sophisticated form of sensor fusion to infer semantic attributes from sensor outputs. Computationally, this translates into the use of a Bayesian network as the core of the content characterization architecture.

6.1 Bayesian Networks

Given a set of random variables X, a fundamental question in probabilistic inference is how to infer the impact on a subset of variables of interest U of the observation of another (non-overlapping) subset of variables O in the model, i.e., the ability to compute P(U | O = o). While this computation is, theoretically, straightforward to perform using

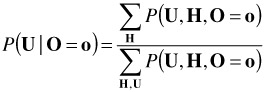
where H = X \ {U U O}, and the summations are over all the possible configurations of the sets H and O; in practice, the amount of computation involved in the evaluation of these summations makes the solution infeasible even for problems of relatively small size. A better alternative is to explore the relationships between the variables in the model to achieve more efficient inference procedures. This is the essence of Bayesian networks.

A Bayesian network for a set of variables X = {X₁, .,. X_n} is a probabilistic model composed of 1) a graph G, and 2) a set of local probabilistic relations P. The graph consists of a set of nodes, each node corresponding to one of the variables in X, and a set of links (or edges), each link expressing a probabilistic relationship between the variables in the nodes it connects. Together, the graph G and the set of probabilities P define the joint probability distribution for X. Denoting the set of parents of the node associated with X₁ by pa₁, this joint distribution is

The ability to decompose the joint density into a product of local conditional probabilities allows the construction of efficient algorithms where inference takes place by propagation of beliefs across the nodes in the network [21,22].

6.2 Bayesian Semantic Content Characterization

Figure 3.7 presents a Bayesian network that naturally encodes the content characterization problem. The set of nodes X is the union of two disjoint subsets: a set S of sensors containing all the leaves (nodes that do not have any children) of the graph, and a set A of semantic content attributes containing the remaining variables. The set of attributes is organized hierarchically, variables in a given layer representing higher level semantic attributes than those in the layers below.

Figure 3.7: A generic Bayesian architecture for content characterization. Even though only three layers of variables are represented in the figure, the network could contain as many as desired ( 1998 IEEE).

The visual sensors are tuned to visual features deemed relevant for the semantic content characterization. The network infers the presence/absence of the semantic attributes given these sensor measurements, i.e., P(a|S), where a is a subset of A. The arrows indicate a causal relationship from higher-level to lower-level attributes and from attributes to sensors and, associated with the set of links converging at each node, is a set of conditional probabilities for the state of the node variable given the configuration of the parent attributes. Variables associated with unconnected nodes are marginally independent.

6.3 Semantic Modelling

One of the strengths of Bayesian inference is that the sensors of Figure 3.7 do not have to be flawless since 1) the model can account for variable sensor precision, and 2) the network can integrate the sensor information to disambiguate conflicting hypothesis. Consider, for example, the simple task of detecting sky in a sports database containing pictures of both skiing and sailing competitions. One way to achieve such a goal is to rely on a pair of sophisticated water and sky detectors. The underlying strategy is to interpret the images first and then characterize the images according to this interpretation.

While such strategy could be implemented with Bayesian procedures, a more efficient alternative is to rely on the model of Figure 3.8. Here, the network consists of five semantic attributes and two simple sensors for large white and blue image patches. In the absence of any measurements, the variables sailing and skiing are independent. However, whenever the sensor of blue patches becomes active, they do become dependent (or, in the Bayesian network lingo, d-connected [21]) and the knowledge of the output of the sensor of white patches is sufficient to perform the desired inference.

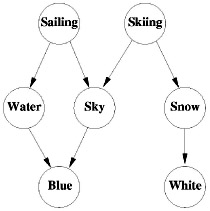
Figure 3.8: A simple Bayesian network for the classification of sports ( 1998 IEEE).

This effect is known as the "explaining away" capability of Bayesian networks [21]. Although there is no direct connection between the white sensor and the sailing variable, the observation of white reduces the likelihood of the sailing hypothesis and this, in turn, reduces the likelihood of the water hypothesis. So, if the blue sensor is active, the network will infer that this is a consequence of the presence of sky, even though we have not resorted to any sort of sophisticated sensors for image interpretation. That is, the white sensor explains away the firing of the blue sensor.

This second strategy relies more in modelling the semantics and the relationships between them than in the classification of the image directly from the image observations. In fact, the image measurements are only used to discriminate between the different semantic interpretations. This has two practical advantages. First, a much smaller burden is placed on the sensors which, for example, do not have to know that "water is more textured than sky," and are therefore significantly easier to build. Second, as a side effect of the sky detection process, we obtain a semantic interpretation of the images that, in this case, is sufficient to classify them into one of the two classes in the database.