3. Models for Temporal Video Structure

Because shot boundaries can be seen as arrivals over discrete, non-overlapping temporal intervals, a Poisson process seems an appropriate model for shot duration [14]. However, events generated by Poisson processes have inter-arrival times characterized by the exponential density, which is a monotonically decreasing function of time. This is clearly not the case for the shot duration, as can be seen from the histograms in Figure 3.2. In this work, we consider two alternative models, the Erlang and Weibull distributions.

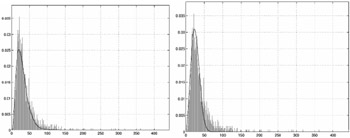
click to expand
Figure 3.2: Shot duration histogram, and maximum likelihood fit obtained with the Erlang (left) and Weibull (right) distributions ( 2000 IEEE).

3.1 The Erlang Model

Letting τ be the time since the previous boundary, the Erlang distribution [14] is described by

It is a generalization of the exponential density, characterized by two parameters: the order r, and the expected inter-arrival time (1/λ) of the underlying Poisson process. When r=1, the Erlang distribution becomes the exponential distribution. For larger values of r, it characterizes the time between the r^th order inter-arrival time of the Poisson process. This leads to an intuitive explanation for the use of the Erlang distribution as a model of shot duration: for a given order r, the shot is modelled as a sequence of r events which are themselves the outcomes of Poisson processes. Such events may reflect properties of the shot content, such as "setting the context" through a wide-angle view followed by "zooming in on the details" when r=2, or "emotional buildup" followed by "action" and "action outcome" when r=3.

Figure 3.2 presents a shot duration histogram, obtained from the training set to be described in section 5.2, and its maximum likelihood (ML) Erlang fit.

3.2 The Weibull Model

While the Erlang model provides a good fit to the empirical density, it is of limited practical utility due to the constant arrival rate assumption [15] inherent to the underlying Poisson process. Because λ is a constant, the expected rate of occurrence of a new shot boundary is the same if 10 seconds or 1 hour have elapsed since the occurrence of the previous one. An alternative model that does not suffer from this problem is the Weibull distribution [15], which generalizes the exponential distribution by considering an expected rate of arrival of new events that is a function of time τ

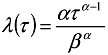
and of the parameters α and β; leading to a probability density of the form

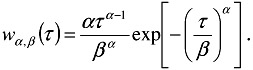
Figure 3.2 presents the ML Weibull fit to the shot duration histogram. Once again we obtain a good approximation to the empirical density estimate.