Appendix

A Proof of Proposition 1

Without loss of generality, let X = {x₁,x₂,…,x_l} and Y = {y₁,y₂,…,y_l} with d(x_i,y_i) ≤ ε for i = 1, 2,…,l. Let Z_i be a binary random variable such that Z_i= 1 if both x_i and y_i are chosen as sampled frames, and 0 otherwise. Since W_m is the total number of similar pairs between the two sets of sampled frames, it can be computed by summing all the Z_i's:

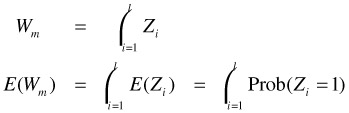
Since we independently sample m frames from each sequence, the probability that Z_i = 1 for any i is (m/l)². This implies that E(W) = m²/l.

B Proof of Proposition 2

To simplify the notation, let ρ(X,Y) = vvs(X,Y;ε) and (X,Y) = vss_b(, , m). For an arbitrary pair of X and Y, we can bound the probability of the event |ρ(X,Y)- (X,Y)| by the Hoeffding Inequality [28]:

(28.19)

To find an upper bound for P_err(m), we can combine (0.1) and the union bound as follows:

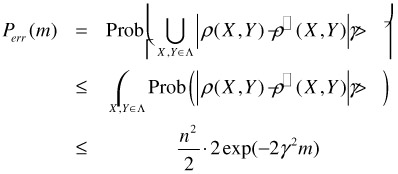
A sufficient condition for P_err(m) ≤ δ is thus

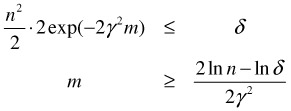
C Proof of Proposition 3

For each term inside the summation on the right hand side of Equation (28.12), d(x, y) must be smaller than or equal to ε. If d(x, y) ≤ ε, our assumption implies that both x and y must be in the same cluster C belonging to both [X]_ε and [Y]_ε. As a result, we can rewrite the right hand side of Equation (28.12) based only on clusters in [X]_ε ⋂ [Y]_ε:

(28.20)

Based on the definition of a Voronoi Cell, it is easy to see that V_X(z)∩V_Y(z) = V_X⋃Y(z) for all z ∈C with C ∈ [X]_ε∩[Y]_ε. Substituting this relationship into Equation (28.12), we obtain:

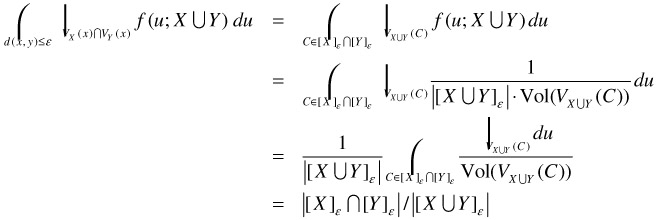
Finally, we note that [X]_ε⋂[Y]_ε is in fact the set of all Similar Clusters in [X⋃Y]_ε, and thus the last expression equals to the IVS. The reason is that for any Similar Cluster C in [X⋃Y]_ε, C must have at least one x ∈ X and one y ∈ Y such that d(x, y) ≤ ε. By our assumption, C must be in both [X]_ε and [Y]_ε.

D Proof of Proposition 4

Without loss of generality, we assume that x₁ is at the origin with all zeros, and x₂ has k 1's in the rightmost positions. Clearly, d(x₁,x₂) = k. Throughout this proof, when we mention a particular sequence Y ∈ Γ, we adopt the convention that Y = {y₁, y₂} with d(x₁,y₁) ≤ ε and d(x₂,y₂) ≤ε.

We first divide the region A into two partitions based on the proximity to the frames in X:

A₁ := {s ∈ A: g_X(s) = x₁} and A₂ := {s ∈ A: g_X(s) = x₂}

We adopt the convention that if there are multiple frames in a video Z that are equidistant to a random vector s, g_Z(s) is defined to be the frame furthest away from the origin. This implies that all vectors equidistant to both frames in X are elements of A₂. Let s be an arbitrary vector in H, and R be the random variable that denotes the number of 1's in the rightmost k bit positions of s. The probability that R equals to a particular r with r ≤ k is as follows:

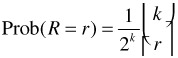
Thus, R follows a binomial distribution of parameters k and 1/2. In this proof, we show the following relationship between A₂ and R:

(28.21)

With an almost identical argument, we can show the following:

(28.22)

Since Vol(A) = Vol(A₁) + Vol(A₂), the desired result follows.

To prove Equation (28.21), we first show if k/2≤R<k/2+ε, then s ∈ A₂. Assuming the definitions for A and A₂, we need to show two things: (1) g_X(s) = x₂; (2) there exists a Y ∈ Γ such that s ∈ G(X,Y;ε), or equivalently, g_Y(s) = y₁. To show (1), we rewrite R = k/2 + N where 0≤N<ε and let the number of 1's in s be L. Consider the distances between s and x₁, and between s and x₂. Since x₁ is all zeros, d(s, x,) = L. As x₂ has all its 1's in the rightmost k position, d(s,x₂) = (L-R) + (k-R) = L + k-2R. Thus,

d(s,x1)-d(s,x2)	=	L-L(+k-2R)
	=	2R-k
	=	2N≥0,

which implies that g_X(s) = x₂. To show (2), we define y₁ to be a h -bit binary number with all zeros, except for ε 1's in the positions which are randomly chosen from the R 1's in the rightmost k bits of s. We can do that because R≥k/2≥ε . Clearly, d(x₁,y₁) = ε and d(s,y₁) = L-ε. Next, we define y₂ by toggling ε out of k 1's in x₂. The positions we toggle are randomly chosen from the same R 1's bits in s. As a result, d(x₂, y₂) = ε and d(s, y₂) = (L-R) + (k-R + ε) = L + ε-2N. Clearly, Y:={y₁,y₂} belongs to Γ. Since

d(s,y2)-d(s,y1)	=	(L + ε-2N)-(L-ε)
	=	2(ε-N)>0

g_Y(s) = y₁ and, consequently, s ∈ G(X,Y;ε).

Now we show the other direction: if s ∈ A₂, then k/2≤ R<k/2+ ε. Since s ∈ A₂, we have g_X(s) = x₂ which implies that L = d(s,x₁)≥d(s,x₂) = L + k-2R or k/2≤R. Also, there exists a Y ∈ Γ with s ∈ G(X, Y; ε). This implies g_Y(s) = y₂, or equivalently, d(s,y_l)<d(s, y₂). This inequality is strict as equality will force g_Y(s) = y₂ by the convention we adopt for g_Y( ). The terms on both sides of the inequality can be bounded using the triangle inequality: d(s,y₁)≥d(s,x₁)-d(x₁,y₁) = L-ε and d(s, y₂)≤d(s, x₂) + d(x₂,y₂) = L + k-2R + ε. Combining both bounds, we have

L-ε<L + k-2R + ε ⇓ R<k/2 + ε

This completes the proof for Equation (28.21). The proof of Equation (28.22) follows the same argument with the roles of x₁ and x₂ reversed. Combining the two equations, we obtain the desired result.

E Proof of Proposition 5

We prove the case for video X and the proof is identical for Y. Since s ∈ G(X,Y;ε), we have d(g_X(s),g_Y(s)) > ε and there exists x ∈ X with d(x,g_Y(s))≤ε. Since all Similar Clusters in [X⋃Y]_ε are ε-compact, g_X(s) cannot be in the same cluster with x and g_Y(s). Thus, we have d(g_X(s), x) > ε. It remains to show that d(x,s)-d(g_X(s),s) ≤ 2ε. Using the triangle inequality, we have

(28.23)

s ∈ G(X,Y;ε) also implies that there exists y ∈ Y such that d(y, g_Y (s)) ≤ ε. By the definition of g_Y (s), d(g_Y (s), s) ≤ d(y,s). Thus, we can replace g_Y (s) with y in Equation (28.23) and combine with the triangle inequality to obtain:

d(x,s)-d(gX(s),s)	≤	ε + d(y,s)-d(gX(s),s)
	≤	ε + d(y,gX(s))
	≤	2ε