5.1 Expectation for Probability Measures

5.1 Expectation for Probability Measures

For definiteness, suppose that 1,000 lottery tickets are sold, numbered 1 through 1,000, and both prizes are guaranteed to be awarded. A world can be characterized by three numbers (a, b, c), each between 1 and 1,000, where a and b are the ticket numbers that are awarded first and second prize, respectively, and c is Alice's ticket number. Suppose that at most one prize is awarded per ticket, so that a ≠ b. The amount of money that Alice wins in the lottery can be viewed as a random variable on this set of possible worlds. Intuitively, the amount that Alice can expect to win is the amount she does win in each world (i.e., the value of the random variable in each world) weighted by the probability of that world. Note that this amount may not match any of the amounts that Alice actually could win. In the case of the lottery, if all tickets are equally likely to win, then the expected amount that Alice can win, according to this intuition, is $1: 999 out of 1,000 times she gets nothing, and 1 out of 1,000 times she gets $1,000. However, she never actually wins $1. It can be shown that, if she plays the lottery repeatedly, then her average winnings are $1. So, in this sense, her expected winnings say something about what she can expect to get in the long run.

The intuition that Alice's expected winnings are just the amount she wins in each world weighted by the probability of that world can be easily formalized, using the notion of the expected value of a gamble. (Recall that a gamble is a real-valued random variable.) If W is finite and every set (and, in particular, every singleton set) is measurable, then the expected value of the gamble X (or the expectation of X) with respect to a probability measure μ, denoted E_μ(X), is just

Thus, the expected value of a gamble is essentially the "average" value of the variable. More precisely, as I said earlier, it is its value in each world weighted by the probability of the world.

If singletons are not necessarily measurable, the standard assumption is that X is measurable with respect to ; that is, for each value x ∊ (X), the set of worlds X = x where X takes on value x is in . Then the expected value of X is defined as

It is easy to check that (5.1) and (5.2) are equivalent if all singletons are measurable and W is finite (Exercise 5.1). However, (5.2) is more general. It makes sense even if W is not finite, as long as (X) is finite. Expectation can be defined even if (X) is infinite using integration rather than summation. Since I want to avoid integration in this book, for the purposes of this chapter, all gambles are assumed to have finite range (i.e., for all gambles X considered in this chapter, (X) is finite).

There are a number of other expressions equivalent to (5.2). I focus on one here. Suppose that (X) = {x₁,…, x_n}, and x₁ < … <x_n. Then

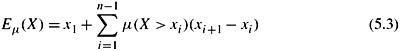
(Exercise 5.2). A variant of (5.3), which essentially starts at the top and works down, is considered in Exercise 5.3.

What is the point of considering a definition of expectation like (5.3), given that it is equivalent to (5.2)? As long as only probability is considered, there is perhaps not much point. But analogues of these expressions for other representations of uncertainty are not, in general, equivalent. I return to this point in Section 5.2.2.

I conclude this section by listing some standard properties of expectation that will be useful in comparing expectation for probability with expectation for other forms of uncertainty. If X and Y are gambles on W and a and b are real numbers, define the gamble aX + bY on W in the obvious way: (aX + bY)(w) = aX(w) + bY(w). Say that X ≤ Y if X(w) ≤ Y(w) for all w ∈ W. Let denote the constant function that always returns c; that is, . Let μ be a probability measure on W.

Proposition 5.1.1

The function E_μ has the following properties for all measurable gambles X and Y.

1. E_μ is additive: E_μ(X + Y) = E_μ(X) + E_μ(Y).

2. E_μ is affinely homogeneous: E_μ(aX + 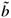) = aE_μ(X) + b for all a, a, b ∊ ℝ.

3. E_μ is monotone: if X ≤ Y, then E_μ(X) ≤ E_μ(Y).

Proof See Exercise 5.4.

The next result shows that the properties in Proposition 5.1.1 essentially characterize probabilistic expectation. (Proposition 5.1.1 is not the only possible characterization of E_μ. An alternate characterization is given in Exercise 5.5.)

Proposition 5.1.2

Suppose that E maps gambles that are measurable with respect to to ℝ and E is additive, affinely homogeneous, and monotone. Then there is a (necessarily unique) probability measure μ on such that E = E_μ.

Proof The proof is quite straightforward; I go through the details here just to show where all the assumptions are used. If U ∊ , let X_U denote the gamble such that X_U (w) = 1 if w ∈ U and X_U(w) = 0 if w ∉ U. A gamble of the form X_U is traditionally called an indicator function. Define μ(U) = E(X_U). Note that X_W = 1, so μ(W) = 1, since E is affinely homogeneous. Since X_∅ is and E is affinely homogeneous, it follows that μ(∅) = E(X_∅) = 0. X_∅ ≤ X_U ≤ X_W for all U ⊆ W ; since E is monotone, it follows that 0 = E(X_∅) ≤ E(X_U) = μ(U) ≤ E(X_W) = 1. If U and V are disjoint, then it is easy to see that X_U∪V = X_U + X_V. By additivity,

Thus, μ is indeed a probability measure.

To see that E = E_μ, note that it is immediate from (5.2) that μ(U) = E_μ(X_U) for U ∊ . Thus, E_μ and E agree on all measurable indicator functions. Every measurable gamble X can be written as a linear combination of measurable indicator functions. For each a ∊ (X), let U_X,a ={w : X(w) = a}. Since X is a measurable gamble, U_X,a must be in . Moreover, X = ∑_a∊(X) aX_UX,a). By additivity and affine homogeneity, E_μ(X) = ∑_a∊(X) aE(X_UX,a). (Here I am using the fact that gambles have finite range, so finite additivity suffices to give this result.) By Proposition 5.1.1, E_μ(X) = ∑_a∊(X) aE_μ(X_UX,a). Since E and E_μ agree on measurable indicator functions, it follows that E(x) = E_μ(x). Thus, E = E_μ as desired.

Clearly, if μ(U) ≠ μ′(U), then E_μ(X_U) ≠ E_μ′(X_U). Thus, μ is the unique probability measure on such that E = E_μ.

If μ is countably additive and W is infinite, then E_μ has a continuity property that is much in the spirit of (2.1):

(Exercise 5.6). (X₁, X₂, … is increasing to X if, for all w ∈ W, X₁(w) ≤ X₂(w) ≤ … and lim_i→∞ X_i(w) = X(w).) This property, together with the others in Proposition 5.1.2, characterizes expectation based on a countably additive probability measure (Exercise 5.6). Moreover, because E_μ(−X) =−E_μ(x), and X₁, X₂, … decreases to X iff −X₁, −X₂, … increases to −X, it is immediate that the following continuity property is equivalent to (5.4):