4.2 Multimedia Index Structures

---

4.2 Multimedia Index Structures

The term indexing usually refers (as applied in the previous section) to the process of assigning terms or phrases that represent the information content of multimedia data. In contrast, the notion of an index from the point of view of a MMDBMS refers to the access structures built on the extracted low- and high-level feature vectors to accelerate data access. Most index access structures make use of multidimensional data structures. A multimedia object is represented, as a result of the indexing process, by an n-dimensional feature vector and, thus, constitutes a point in a multidimensional space. ^[68], ^[69], ^[70] Finding images similar to a query image involves retrieving those images whose corresponding locations in the n-dimensional space are within some measure of proximity to the point corresponding to the query object. This process is commonly referred to as similarity search.

Many works ^[71], ^[72], ^[73], ^[74], ^[75], ^[76], ^[77], ^[78] are dedicated to the proposal of efficient methods for implementing the similarity search. The increasing need in applications to be able to store complex feature vectors, that is, high-dimensional vectors with more than 100 elements, and to index them based on their content has triggered a lot of research on multidimensional index structures, such as, for instance, those structures proposed in Chakrabarti and Mehrotra, ^[79] Cha and Chung, ^[80] White and Jain, ^[81] Kurniawati et al., ^[82] and Cha et al. ^[83] The solutions proposed focusing on two main issues. The first solution class intends to reduce the dimension of the feature vectors, using transformation techniques like the Karhunen-Loeve Transform, Discrete Cosine Transform-based reduction methods or clustering techniques and then applying well-known indexing techniques. The second solution is the use of special indexing structures, such as the GC (Grid Cell)-trees, which may store and search efficiently long feature vectors as data points and that allow an effective partitioning of the large data space.

Existing multidimensional data structures for feature spaces can be classified into Data Partitioning (DP)-based and Space Partitioning (SP)-based structures. ^[84] A DP-based index structure consists of bounding regions (BRs) arranged in a spatial containment hierarchy. At the data level, the nearby points are clustered within BRs. At higher levels, nearby BRs are recursively clustered within bigger BRs, thus forming a hierarchical directory structure. The BRs can be bounding boxes, for example, R-trees ^[85] and X-trees; ^[86] or bounding spheres or diamonds, for example, SS-trees ^[87], ^[88] M-trees, ^[89] and TV-trees. ^[90] In contrast, an SP-based index structure consists of space recursively partitioned into mutually disjoint subspaces. The hierarchy of partitions forms a tree structure (e.g., KDB-trees ^[91] and hB-trees ^[92]) and the GC-tree for high-dimensional feature vector spaces. ^[93] The data partitioning is, in most cases, based on the values of the feature vectors along each dimension in the feature space. ^[94] This data partitioning is independent of the distance function used to compute the distance among objects in the database or between the query object and the database objects. Examples are R-trees and X-trees, as well as hB-trees. However, for SS-trees, the partitioning is based on the distance from one or more pivot points of the BRs.

Multidimensional data structures are also used to represent spatial and temporal relationships. ^[95], ^[96] For instance, there are two major approaches to describing the spatial content of images: first, spatial content that is directional, and second, topological relationships between the domain objects. In the first approach, a single content element or structure captures the spatial content. In the second approach, several content elements collectively capture pair-wise spatial relationships between the domain objects. In both approaches, an algorithm is used to compute spatial similarity between two images. Some algorithms, based on the second approach, perform logical deduction or reduction before applying a similarity algorithm.

The assumption of most related works is that all elements of the feature vector are numeric. However, many vector elements are nonnumeric, and the domains are unordered. This introduces an additional problem of mapping the existing vector elements into a numeric domain. However, it may not be possible to find numerical substitutes for all contents. Furthermore, in perspective of the evolving number of extraction tools, more and more feature vectors will be extracted and have to be queried together. This query type is commonly referred to as a multifeature query. ^[97], ^[98] Developing effective query processing techniques for high-dimensional multifeature queries is an open research issue. Finally, continuous nearest-neighbor (NN) search became of interest in the context of mobile spatial databases. Queries like, "give me all nearest hotels when I travel from Vienna to Hamburg" cannot be efficiently answered by subsequent k-NN search queries. Toa et al. ^[99] recently tackled this problem.

4.2.1 Use Case Study: The GC-Tree and the Curse of Dimensionality

With the proliferation of multimedia data and more accurate indexing methods, the feature vectors of low- and high-level multimedia describing features tend to have high dimensionalities, say, over 100. For instance, the Scalable Color Descriptor in MPEG-7, as described in Section 2.5.3, may scale to 256 values. So the main issue is to overcome the curse of dimensionality—a phenomenon in which the performance of indexing methods degrades drastically as the dimensionality increases. ^[100]

One promising solution to the dimensionality problem is the use of a vector approximation-based indexing method, namely, the LPC (Local Polar Coordinate) file ^[101] and the VA (vector approximation) file. ^[102] The vector-based search on a VA file is based on a simple filtering process. It eliminates those vectors that are considered worse than the first n vectors encountered during the sequential scan of the entire data file. This is accomplished by comparing the "lower bound" of a query vector with all the vectors in the file and storing potential records in a memory store; these records are considered to be within the acceptable region of the query vector. If a record satisfies the lower bound requirement, it will then be compared with the query item by computing the actual distance between them.

Although the LPC and VA file provided significant improvements compared with previous partitioning techniques, it suffers from performance degradation if the dataset is highly clustered because it employs a simple space partitioning strategy and a uniform bit allocation strategy for representing the partitioned region. ^[103] In this context, Cha and Chung ^[104] proposed the GC-tree indexing structure. The GC-tree is a SP-method that partitions the data space based on the analysis of the data distribution density; that is, it focuses the partitioning on the dense subspaces and dynamically constructs an index that reflects the partition hierarchy.

Exhibit 4.7 shows the difference between a typical SP method and a DP method based on the GC-tree. The DP method partitions the space by identifying BRs around the data points, and the SP method partitions the space recursively according to the density function.

Exhibit 4.7: Data partitioning and space partitioning strategies.

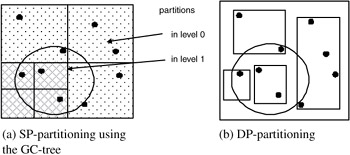
The GC-tree consists of two components: directory nodes and data nodes. Directory nodes are employed for indexing the space partitioning, and data nodes are used for storing real objects. Each directory node corresponds to a region (cell) in the data space. Two types of regions are distinguished: those corresponding to clusters and those corresponding to outlier regions. The region corresponding to the cluster is a hyperrectangle with sides of equal length. The outlier region is the region remaining after removing the regions for clusters from the original region.

The GC-tree employs a density-based approach to partition the data space and to determine the number of bits to represent a cell vector for a partition. To approximate the density of the data points, the GC-tree partitions the data space into nonoverlapping hypersquare cells and counts the points that lie inside each cell of the partition—partitioning every dimension into the same number of equal length intervals at one time accomplishes this. This means that every cell generated from the partition of a space has the same volume, and therefore, the number of points inside a cell can be used to approximate the density of the cell.

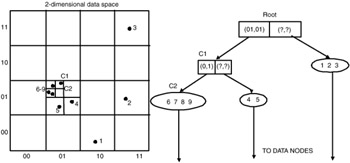
Example: As an example, consider the two-dimensional GC-tree with a four-level index in Exhibit 4.8. At left, the two-dimensional data space is partitioned into 4 × 4 cells by using 2 bits per dimension as representation. At right, the directory nodes of the corresponding GC-tree are shown. The root directory contains two entries: the first from the left points to nodes that represents clusters, the second directory points to an outline region containing the singular points 1, 2, and 3. The directory entry with the cell vector (01, 01) in root points to the node C1 and represents the cell C1, which in turn forms a finer partition into an outlier region that contains the points 4 and 5 and another cluster, C2.

Exhibit 4.8: Example of a grid cell-tree. Nonuniform partition of the data space (left) and index tree (right).

The k-NN search is implemented as a branch and bound search approach (similar to that employed in the R- and X-tree), and the search in the data points is based on the vector-filtering technique from the VA files. The combination of these two techniques shows the advantage for high-dimensional vector spaces, and Cha and Chung ^[105] could demonstrate a performance increase for real image datasets taken from the IBM QBIC (Query by Image Content) stamp image database (see Section 4.4).

^[68]Roussopoulos, N., Kelley, S., and Vincent, F., Nearest neighbor queries, in Proceedings of ACM-SIGMOD Conference on Management of Data, San Jose, June 1995, pp. 71–79.

^[69]Berchtold, S., Bohm, C., Keim, D.A., and Kriegel, H.P., A cost model for nearest neighbor search in high-dimensional data space, in Proceedings of the ACM PODS Conference, Tucson, May 1997, pp. 78–86.

^[70]Pramanik, S., Alexander, S., and Li, J., An efficient searching algorithm for approximate nearest neighbor queries in high dimensions, in IEEE International Conference on Multimedia Computing and Systems, Vol. 1, Florence, Italy, June 1999, pp. 865–869.

^[71]Li, J.Z., Özsu, M.T., Szafron, D., and Oria, V., MOQL: a multimedia object query language, in 3rd International Workshop on Multimedia Information Systems, Como, September 1997, Springer-Verlag, Heidelberg, LNCS Series, pp. 19–28.

^[72]Excalibur Image DataBlade Module User's Guide, Version 1.2, Informix Press, 1999.

^[73]Oracle9i interMedia Audio, Image, and Video User's Guide and Reference, http://technet.oracle.com.

^[74]Evangelidis, G., Lomet, D., and Salzberg, B., The hB tree: a multi-attribute index supporting concurrency, recovery and node consolidation. VLDB J., 6, 1–25, 1997.

^[75]Ciaccia, P., Patella, M., and Zezula, P., M-Tree: an efficient access method for similarity search in metric spaces, in Proceedings of the VLDB Conference, Athens, August 1997, pp. 426–435.

^[76]Chakrabarti, K. and Mehrotra, S., The hybrid tree: an index structure for high dimensional feature spaces, in Proceedings of the International Conference on Data Engineering (ICDE), Sydney, March 1999, pp. 440–447.

^[77]Cha, G.-H. and Chung, C.-W., The GC-Tree: a high-dimensional index structure for similarity search in image databases, IEEE Trans. Multimedia, 4, 235–247, 2002.

^[78]Tao, Y., Papadias, D., and Shen, Q., Continuous nearest neighbor search. International Conference on VLDB 2002, Hong Kong, August 2002, pp. 287–298.

^[79]Chakrabarti, K. and Mehrotra, S., The hybrid tree: an index structure for high dimensional feature spaces, in Proceedings of the International Conference on Data Engineering (ICDE), Sydney, March 1999, pp. 440–447.

^[80]Cha, G.-H. and Chung, C.-W., The GC-Tree: a high-dimensional index structure for similarity search in image databases, IEEE Trans. Multimedia, 4, 235–247, 2002.

^[81]White, D.A. and Jain, R., Similarity indexing with the SS-tree, in Proceedings of the 12th IEEE Intl. Conference on Data Engineering, New Orleans, February 1996, pp. 516–523.

^[82]Kurniawati, R., Jin, J.S., and Shepherd, J.A., The SS+-tree: an improved index structure for similarity searches in a high-dimensional feature space, in Proceedings of the SPIE storage and Retrieval of Image and Video Databases, San Jose, February 1997, pp. 110–120.

^[83]Cha, G.-H., Zhu, X., Petkovic, D., and Chung, C.-W., An efficient indexing method for nearest neighbor searches in high-dimensional image databases, IEEE Trans. Multimedia, 4, 76–87, 2002.

^[84]Chakrabarti, K. and Mehrotra, S., The hybrid tree: an index structure for high dimensional feature spaces, in Proceedings of the International Conference on Data Engineering (ICDE), Sydney, March 1999, pp. 440–447.

^[85]Guttman, A., R-trees: a dynamic index structure for spatial searching, in Proceedings of ACM SIGMOD Conference of Management of Data, Boston, June 1984, pp. 47–57.

^[86]Berchtold, S., Keim, D.A., and Kriegel, H.-P., The X-tree: an indexing structure for high-dimensional data, in Proceedings of the VLDB Conference, Bombay, September 1996, pp. 28–39.

^[87]White, D.A. and Jain, R., Similarity indexing with the SS-tree, in Proceedings of the 12th IEEE Intl. Conference on Data Engineering, New Orleans, February 1996, pp. 516–523.

^[88]Kurniawati, R., Jin, J.S., and Shepherd, J.A., The SS+-tree: an improved index structure for similarity searches in a high-dimensional feature space, in Proceedings of the SPIE storage and Retrieval of Image and Video Databases, San Jose, February 1997, pp. 110–120.

^[89]Ciaccia, P., Patella, M., and Zezula, P., M-Tree: an efficient access method for similarity search in metric spaces, in Proceedings of the VLDB Conference, Athens, August 1997, pp. 426–435.

^[90]Lin, E.T., Omiecinski, E.R., and Yalamanchili, S., Large join optimization on a hypercube multiprocessor. IEEE Trans. Knowl. Data Eng., 6(2), 304–315, 1994.

^[91]Robinson, J.T., The K-D-B tree: a search structure for large multidimensional dynamic indexes, in Proceedings of ACM-SIGMOD International Conference on Management of Data, April 1981, pp. 10–18.

^[92]Evangelidis, G., Lomet, D., and Salzberg, B., The hB tree: a multi-attribute index supporting concurrency, recovery and node consolidation. VLDB J., 6, 1–25, 1997.

^[93]Cha, G.-H. and Chung, C.-W., The GC-Tree: a high-dimensional index structure for similarity search in image databases, IEEE Trans. Multimedia, 4, 235–247, 2002.

^[94]Chakrabarti, K. and Mehrotra, S., The hybrid tree: an index structure for high dimensional feature spaces, in Proceedings of the International Conference on Data Engineering (ICDE), Sydney, March 1999, pp. 440–447.

^[95]Wang, W., Yang, J., and Muntz, R.R., PK-tree: a spatial index structure for high dimensional point data. Technical Report 980032, Computer Science Department, University of California, Los Angeles, September 22, 1998.

^[96]Kim, B. and Um, K., 2d+ string: a spatial metadata to reason topological and directional relationships, in Proceedings of the 11th International Conference on Scientific and Statistical Database Management, Cleveland, July 1999, IEEE CS Press, pp. 112–121.

^[97]Goh, S.-T. and Tan, K.-L., MOSAIC: a fast multi-feature image retrieval system. Data Knowl. Eng., 33, 219–239, 2000.

^[98]Guntzer, U., Balke, W.-T., and Kiesling, W., Optimizing multi-feature queries for image databases, in Proceedings of the International Conference on Very Large Databases, Cairo, September 2000, pp. 419–428.

^[99]Tao, Y., Papadias, D., and Shen, Q., Continuous nearest neighbor search. International Conference on VLDB 2002, Hong Kong, August 2002, pp. 287–298.

^[100]Cha, G.-H., Zhu, X., Petkovic, D., and Chung, C.-W., An efficient indexing method for nearest neighbor searches in high-dimensional image databases, IEEE Trans. Multimedia, 4, 76–87, 2002.

^[101]Cha, G.-H., Zhu, X., Petkovic, D., and Chung, C.-W., An efficient indexing method for nearest neighbor searches in high-dimensional image databases, IEEE Trans. Multimedia, 4, 76–87, 2002.

^[102]Weber, R., Schek, H.-J., and Blott, S., A quantitative analysis and performance study for similarity-search methods in high-dimensional spaces, International Conference on VLDB 1998, New York, August 1998, pp. 194–205.

^[103]Cha, G.-H. and Chung, C.-W., The GC-Tree: a high-dimensional index structure for similarity search in image databases, IEEE Trans. Multimedia, 4, 235–247, 2002.

^[104]Cha, G.-H. and Chung, C.-W., The GC-Tree: a high-dimensional index structure for similarity search in image databases, IEEE Trans. Multimedia, 4, 235–247, 2002.

^[105]Cha, G.-H. and Chung, C.-W., The GC-Tree: a high-dimensional index structure for similarity search in image databases, IEEE Trans. Multimedia, 4, 235–247, 2002.

---