Must-Know Concepts

Must-Know Concepts

Learning the concepts in the following sections is important to your satisfaction with this book. These are the things you must know to work efficiently with the registry. For example, the registry is filled with hexadecimal numbers, and if you don't understand hexadecimal, they're not going to make sense to you. If you're a programmer, you can probably skip these sections; otherwise, don't.

The following sections walk you through the most important of these concepts, beginning with security and globally unique identifiers (GUIDs). You learn how to read hexadecimal numbers, convert them to binary and decimal notation, and use them as bit masks. You learn the difference between Unicode and ANSI character encoding. You even learn how Intel-based computers store numbers in memory. All these topics are significant to your ability to use the registry as a tool.

Security Identifiers

Computer accounts, user accounts, groups, and other security-related objects are security principles. Security Identifiers (SIDs) uniquely identify security principles. Each time Windows and Active Directory create a security principle, they generate a SID for it. The Windows Local Security Authority (LSA) generates SIDs for local security principles and then stores them in the local security database. The Domain Security Authority generates SIDs for domain security principles and then stores them in Active Directory. SIDs are unique within their scope. Every local security principle's SID is unique on the computer, and every domain security principle's SID is unique within any domain in the enterprise. What's more, Windows and Active Directory never reuse a SID, even if they delete the security principle to which that SID belonged. Thus, if you delete an account and then add it back, the account gets a new SID.

The important thing to remember is that every account has a SID. It's like having a passport number that uniquely identifies you to immigration. You can refer to an account by its name or by its SID, but in practice you seldom use the SID because its format is cumbersome. You frequently see accounts' SIDs in the registry, though, and that's why you're learning about them here.

An example of a SID is S-1-5-21-2857422465-1465058494-1690550294-500. A SID always begins with S-. The next number identifies the SID's version—in this case, version 1. The next number indicates the identifier authority and is usually 5, which is NT Authority. The string of numbers up to 500 is the domain identifier, and the rest of the SID is a relative identifier, which is the account or group. This is a very rough overview of the SID format, which is much more complex than this brief example characterizes. If you want to learn more about SIDs, see http://msdn.microsoft.com/library/default.asp?url=/library/en-us/secauthz/security/security_identifiers.asp.

Some SIDs, such as S-1-5-18, are shorter than the one in the previous example. These are well-known SIDs, and they are the same on every computer and in every domain. They are interesting because they pop up over and over again in the registry and in other places. Table 1-1 describes the SIDs well known by Windows. I've italicized the names of SIDs that are of particular relevance to you while you're reading this book. The placeholder domain is the SID's domain identifier.

Table 1-1 Well-Known SIDs

SID	User or Group Name
S-1-0	Null Authority
S-1-0-0	Nobody
S-1-1	World Authority
S-1-1-0	Everyone
S-1-2	Local Authority
S-1-2-0	Local
S-1-3	Creator
S-1-3-0	Creator Owner
S-1-3-1	Creator Group
S-1-3-2	Creator Owner Server
S-1-3-3	Creator Owner Group
S-1-4	Nonunique Authority
S-1-5	NT Authority
S-1-5-1	Dialup
S-1-5-2	Network
S-1-5-3	Batch
S-1-5-4	Interactive
S-1-5-5-X- Y	Logon Session
S-1-5-6	Service
S-1-5-7	Anonymous
S-1-5-8	Proxy
S-1-5-9	Enterprise Domain Controllers
S-1-5-10	Self
S-1-5-11	Authenticated Users
S-1-5-12	Restricted
S-1-5-13	Terminal Service User
S-1-5-14	Remote Interactive Logon
S-1-5-18	LocalSystem or System
S-1-5-19	LocalService
S-1-5-20	NetworkService
S-1-5- domain-500	Administrator
S-1-5- domain-501	Guest
S-1-5- domain-502	krbtgt
S-1-5-domain-512	Domain Admins
S-1-5-domain-513	Domain Users
S-1-5-domain-514	Domain Guests
S-1-5-domain-515	Domain Computers
S-1-5-domain-516	Domain Controllers
S-1-5-domain-517	Cert Publishers
S-1-5-root domain-518	Schema Admins
S-1-5-root domain-519	Enterprise Admins
S-1-5-root domain-520	Group Policy Creator Owners
S-1-5- domain-553	RAS and IAS Servers
S-1-5-32-544	Administrators
S-1-5-32-545	Users
S-1-5-32-546	Guests
S-1-5-32-547	Power Users
S-1-5-32-548	Account Operators
S-1-5-32-549	Server Operators
S-1-5-32-550	Print Operators
S-1-5-32-551	Backup Operators
S-1-5-32-552	Replicator
S-1-5-32-554	Pre-Windows 2000 Compatible Access
S-1-5-32-555	Remote Desktop Users
S-1-5-32-556	Network Configuration Operators
S-1-6	Site Server Authority
S-1-7	Internet Site Authority
S-1-8	Exchange Authority
S-1-9	Resource Manager Authority

Globally Unique Identifiers

Globally unique identifiers are better known as GUIDs (pronounced goo ids). They are numbers that uniquely identify objects such as computers, program components, and devices. These objects often have names, but their GUIDs remain unique even if two of the objects have the same name or if their names change. In other words, an object's GUID is similar to a security principle's SID. You will see GUIDs scattered all over the registry, so you should become familiar with them.

All GUIDs have the same interesting format. They're 16-byte hexadecimal numbers in groups of 8, 4, 4, 4, and 12 digits (0 through 9 and A through F). A dash divides each group of digits, and curly brackets enclose the whole number. An example of a real GUID is {645FF040-5081-101B-9F08-00AA002F954E}, which represents the Recycle Bin object that you see on the desktop. The GUID {127A89AD-C4E3-D411-BDC8-001083FDCE08} belongs to one of the computers in my lab.

Programmers often use the Microsoft tool Guidgen.exe to create GUIDs, but Windows generates them, too. Regardless of the source, Microsoft guarantees that GUIDs are globally unique—hence their name. No matter how many times Guidgen.exe or Windows generates a GUID, the result is always unique. That's what makes GUIDs perfect for identifying objects like computers and devices.

Hexadecimal Notation

Ninety-nine percent of the data you see in the registry is in hexadecimal notation. Computers use hexadecimal rather than decimal notation for a good reason, which you'll learn in a bit. You must learn how to read and convert hexadecimal numbers in order to use the registry as an effective tool. And that's the focus of this section.

Binary and decimal notations don't interchange well. You probably learned decimal notation as a child. In this notation, 734 is 7 x 10² + 3 x 10¹ + 4 x 10⁰, which is 7 x 100 + 3 x 10 + 4 x 1. Easy enough, right? The digits are 0 through 9, and because you multiply each digit right to left by increasing powers of 10 (10⁰, 10¹, 10², and so on), this notation is called base 10. The problem is that decimal notation doesn't translate well into the computer's system of ones and zeros. Binary notation does. In this notation, 1011 is 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰ or 1 x 8 + 0 x 4 + 1 x 2 + 1 x 1 or 11. The digits are 0 and 1, and because you multiply each digit right to left by increasing powers of 2 (2⁰, 2¹, 2 ², and so on), this notation is called base 2. Converting a binary number to a decimal number is a lot of work, and binary numbers are too cumbersome for people to read and write.

That brings us to hexadecimal notation. Hexadecimal notation is base 16, and because you can evenly divide 16 by 2, converting between binary and hexadecimal is straightforward. The digits are 0 through 9 and A through F. Table 1-2 shows the decimal equivalent of each digit. In hexadecimal, A09C is 10 x 16³ + 0 x 16² + 9 x 16¹ + 12 x 16⁰ or 10 x 4096 + 0 x 256 + 9 x 16 + 12 x 1, or 41,116 in decimal notation. As in the other examples, you multiply each hexadecimal digit right to left by increasing powers of 16 (16⁰, 16¹, 16², and so on).

Table 1-2 Hexadecimal Digits

Binary	Hexadecimal	Decimal
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

Converting between binary and hexadecimal notations might be straightforward, but it is also time consuming, so Table 1-2 offers a solution. When converting from binary to hexadecimal, use Table 1-2 to look up each group of four digits from left to right, and jot down its hexadecimal equivalent. For example, to convert 01101010 to hexadecimal, look up 0110 to get 6, and then look up 1010 to get A, so that you end up with the hexadecimal number 6A. If the number of digits in the binary number isn't evenly divisible by 4, just pad the left side with zeros. To convert hexadecimal numbers to binary, use Table 1-2 to look up each hexadecimal digit from left to right, and jot down its binary equivalent. For example, to convert 1F from hexadecimal to binary, look up 1 to get 0001, look up F to get 1111, and string them together to get 00011111.

One last problem: Is 12 a decimal number or a hexadecimal number? You don't have enough information to know for sure. The solution is to always use the prefix 0x at the beginning of hexadecimal numbers. Then 0x12 is a hexadecimal number, whereas 12 is a decimal number. This is the standard format for hexadecimal numbers, and it's the format that Microsoft uses in its documentation and in all the tools you'll use in this book.

TIP
If converting binary, hexadecimal, and decimal numbers is too much work for you, as it certainly is for me, use the Windows Calculator. Click Start, All Programs, Accessories, and Calculator. Make sure you change to scientific view by clicking Scientific on the View menu. In the top left part of Calculator's window, you see four buttons: Hex, Dec, Oct, and Bin. Click the button corresponding to the notation in which you want to input a number, type the number, and then click the button corresponding to the notation to which you want to convert the number. You can also use Registry Editor to toggle between decimal and hexadecimal notations when editing certain types of values.

Bits and Bit Masks

You now understand binary and hexadecimal notations, and now you need to know about bit masks. In the registry, Windows sometimes groups settings together in one number. Each bit within that number is a different setting. Thus, you can store eight settings in a byte, 16 settings in a word, and so on. In this book and elsewhere, you'll see instructions that tell you that a setting's bit mask is 0x20, which simply means that you turn on that setting by enabling the bits that 0x20 represents. This will make more sense as you read on.

You count a binary number's bits from right to left, starting with 0. The number in Figure 1-3 is 0x26. The top part shows the binary equivalent, and the second part shows each bit's number. The bit on the far right is bit 0. In this example, bits 1, 2, and 5 are 1, whereas the remaining bits are 0. If you saw instructions that told you to turn on bit 7, you'd change the number to 10100110. When dealing with bits, a binary 1 is the same thing as “yes” or “true,” and a binary 0 is the same thing as “no” or “false.” In other words, they are Boolean values.

Many times, instructions you read won't give you an exact bit number, so you have to do some math. Often, all you'll see is a bit mask, and you'll have to figure out which bits the mask actually represents. For example, to turn on bit 0x40 in the number 0x43, convert both numbers to binary, figure out which bits the mask represents, change those bits to ones in the number, and then convert the number back to hexadecimal. Using Calculator in scientific view is the easiest way to perform these steps. You'd follow the same steps to turn off the setting, except that you'd change the target bits to 0. After a while, you get pretty good at figuring out which bits a mask represents. Moving from right to left, each bit's mask is 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, and 0x80. The bottom part of Figure 1-3 illustrates this.

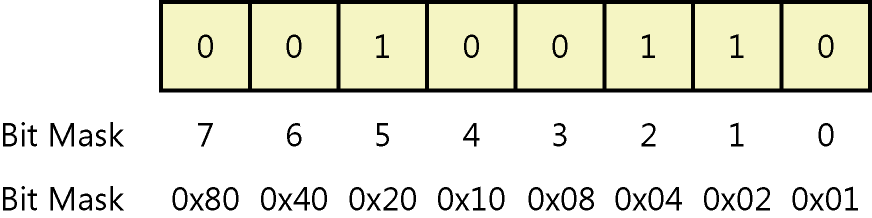
Figure 1-3 You count bits moving from right to left.

NOTE
Turning bit masks on and off is even easier if you use bitwise math. To turn on a bit mask in a number, OR the two numbers together. To turn a bit mask off in a number, reverse the bits in the mask, and then AND it together with the number: number AND NOT mask. Using Calculator in scientific view supports all these operations. AND, OR, and NOT are Boolean logic operations. To learn more about these operations, visit the following Web site. http://www.techweb.com/encyclopedia/defineterm.jhtml?term=boolean+logic&x=47&y=11

Little-Endian and Big-Endian

In a hexadecimal number such as 0x0102, the 0x01 is the most significant byte, and the 0x02 is the least significant. The leftmost bytes are more significant because you multiply these digits by a higher power of 16. The rightmost digits are less significant, so the digits become more significant as you move from right to left.

Programs store numbers in memory in two ways: big-endian or little-endian. When a program stores a number using big-endian ( big end first) storage, it stores the most significant bytes in memory first, followed by the less significant bytes. When stored in memory using big-endian storage, the number 0x01020304 is 0x01 0x02 0x03 0x04. It makes sense, doesn't it? However, Intel-based processors use the little-endian (little end first) architecture, which means they store the least significant bytes first, followed by the more significant bytes. Thus, the number 0x01020304 is 0x04 0x03 0x02 0x01 in memory.

Although most of the tools you'll use display all numbers—little-endian or big-endian—correctly, you'll have to pay careful attention when you're looking at numbers in binary values, because the tools won't automatically reverse the order of the bytes for you. Thus, if you see the number 0x34 0x77 in a binary value, you'll have to remember to reverse the order of bytes to get the result 0x7734.

ANSI and Unicode Encoding

The first prominent character-encoding scheme (how a computer represents text) was ASCII, and it's still in use today. In ASCII character encoding, each character is eight bits, or a single byte. Because ASCII was for western languages, its use was limited in European countries and regions whose languages contained characters that weren't included in the 256 characters that ASCII supported. To get around this limitation, the International Standards Organization (ISO) created a new character-encoding standard called Latin-1, which included European characters left out of the ASCII set. Microsoft enhanced Latin-1 and called this new standard ANSI. But ANSI is still an 8-bit character encoding that can represent only 256 unique characters. Many languages have thousands of symbols, particularly Asian languages such as Chinese, Korean, and Japanese.

To overcome the limitations of an 8-bit character-encoding standard, Microsoft, partnering with companies such as Apple Computer, Inc., and IBM, created the non-profit consortium Unicode, Inc., to define a new character-encoding standard for international character sets. The work done at Unicode merged with work already in progress at ISO, and the result was the Unicode standard for character encoding. Unicode is a 16-bit encoding standard, which provides for 65,536 unique characters—more than enough to represent all of the world's languages. It even supports arcane languages, such as Sanskrit and Egyptian hieroglyphs, and includes punctuation marks, mathematical symbols, and graphical symbols.

Unicode is the character encoding that is native to Windows, but Windows also supports ANSI. Internally, the operating system represents object names, paths, and file names as 16-bit Unicode characters. It also usually stores data in the registry using Unicode. If a program stores the text Jerry using ANSI, it looks like 0x4A 0x65 0x72 0x72 0x79 in memory. However, if the program stores the same string using Unicode, it looks like 0x4A 0x00 0x65 0x00 0x72 0x00 0x72 0x00 0x79 0x00 in memory. Why? Because Unicode text is 16-bit numbers, which Windows stores in little-endian format. (See “Little-Endian and Big-Endian” earlier in this chapter.) Thus, it writes the J into memory as 0x004A (with the bytes reversed), followed by the e as 0x0065, and then the remaining characters as 0x0072, 0x0072, and 0x0079.

Null and Empty Strings

If you've written programs using a language such as C, the concept of null isn't foreign to you. Null is 0x00, or the null character. Windows terminates strings with the null character so that programs know where strings end.

In the registry, a similar concept is that a value can have null data, meaning that it contains no data at all. It's empty. Usually, when you're looking at the null value in the registry, you see the text (value not set). This is different from a value that contains an empty string—text that's zero characters in length, or "". The following values are not the same:

• Null

• ""