Using the Solver to Set Quantity and Pricing

Previous page
Table of content
Next page

When your forecasting problem contains more than one variable, you need to use the Solver add-in utility to analyze the scenario. Veterans of business school will happily remember multivariable case studies as part of their finance and operations management training. While a full explanation of multivariable problem solving and optimization is beyond the scope of this book, you don't need a business-school background to use the Solver command to help you decide how much of a product to produce, or how to price goods and services. We'll show you the basics in this section by illustrating how a small coffee shop determines which coffee beverages it should sell, and what its potential revenue will be.

In our example, we're running a coffee shop that currently sells three beverages: regular fresh-brewed coffee, premium caffè latte, and premium caffè mocha. We currently price regular coffee at $1.25, caffè latte at $2.00, and caffè mocha at $2.25, but we're not sure what our revenue potential is and what emphasis we should give to each of the beverages. (Although the premium coffees bring in more money, their ingredients are more expensive, and they're more time-consuming to make than regular coffee.) We can make some basic calculations by hand, but we want to structure our sales data in a worksheet so that we can add to it periodically and analyze it using the Solver.

NOTE
The Solver is an add-in utility, so you should verify that it's installed on your system before you get started. If the Solver command isn't on your Tools menu, choose Add-Ins from the Tools menu, and select the Solver Add-In option in the Add-Ins dialog box. If Solver isn't in the list, you'll need to install it by running the Office Setup program again and selecting it from the list of Excel add-ins. For more information, see "Installing Add-In Commands and Wizards"

Setting Up the Problem

The first step in using the Solver command is to build a worksheet that is Solver-friendly. This involves creating a target cell to be the goal of your problem— for example, a formula that calculates total revenue that you want to maximize— and assigning one or more variable cells that the Solver can change to reach your goal. Your worksheet can also contain other values and formulas that use the target cell and the variable cells. In fact, each of your variable cells must be precedents of the target cell for the Solver to do its job. (In other words, the formula in the target cell must depend on the variable cells for part of its calculation.) If you don't set it up this way, when you run the Solver you'll get the error message, The Set Target Cell values do not converge.

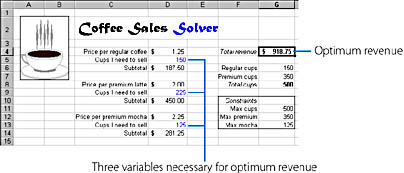
Figure 23-3 shows a simple worksheet that can be used to estimate the weekly revenue for our example coffee shop and to determine how many cups of coffee we will need to sell. Cell G4 is the target cell that calculates the total revenue that the three coffee drinks generate. The three lines that converge in cell G4 were drawn by the Trace Precedents command on the Auditing submenu of the Tools menu. They show how the formula in cell G4 depends on three other calculations for its result. (The Auditing submenu contains commands that help track the links between formulas in a worksheet.) The three variable cells in the worksheet are cells D5, D9, and D13— these are the values we want the Solver to determine when it finds an optimum solution to maximizing our weekly revenue.

ON THE WEB
The Solver.xls example is on the Running Office 2000 Reader's Corner page.

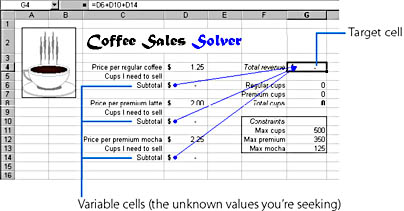
click to view at full size.

Figure 23-3. Before you use the Solver command, you need to build a worksheet that has a target cell and one or more variable cells. The Auditing submenu can help you visualize the relationship between cells.

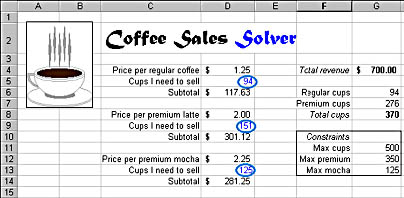
In the bottom right corner of our screen is a list of constraints we plan to use in our forecasting. A constraint is a limiting rule or guiding principle that dictates how the business is run. For example, because of storage facilities and merchandising constraints, we're currently able to produce only 500 cups of coffee (both regular and premium) per week. In addition, our supply of chocolate restricts the production of caffè mochas to 125 per week, and a milk refrigeration limitation restricts the total production of premium coffee drinks to 350 per week.

These constraints will structure the problem, and we'll enter them in a special dialog box when we run the Solver command. Your worksheet must contain cells that calculate the values used as constraints (in this example, G6 through G8). The limiting values for the constraints are listed in cells G11 through G13. Although listing the constraints isn't necessary, it makes the worksheet easier to follow.

TIP
Name Key Cells

If your Solver problem contains several variables and constraints, you'll find it easiest to enter data if you name key cells and ranges in your worksheet by using the Define command on the Name submenu of the Insert menu. Using cell names also makes it easy to read your Solver constraints later. For more information about naming, see "Using Range Names in Functions"

Running the Solver

After you have defined your forecasting problem in the worksheet, you're ready to run the Solver add-in. The steps that follow show you how to use the Solver to determine the maximum weekly revenue for your coffee shop given the following constraints:

In addition to the maximum revenue, the Solver will tell you the optimum distribution of coffees in the three coffee groups. Complete these steps:

  1. Click the target cell— the one containing the formula that is based on the variable cells you want the Solver to determine— in your worksheet. In Figure 23-3, the target cell is G4.

  2. From the Tools menu, choose Solver.

    3. The Solver Parameters dialog box opens, as shown here. Because you clicked the target cell in step 1, the Set Target Cell text box contains the correct reference. The correct Equal To option button (Max) is also selected, because you want to find the maximum value for the cell.

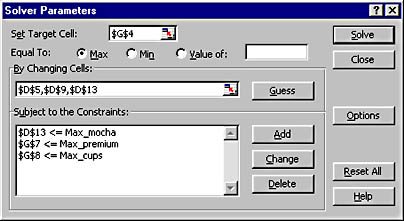
    click to view at full size.

  3. Highlight the By Changing Cells text box. Drag the dialog box to the right so that you can see the variable cells in your worksheet. Select each of the variable cells. If the cells adjoin one another, simply select the group by dragging across the cells. If the cells are noncontiguous, hold down the Ctrl key and click each cell. This will place a comma between each cell entry in the text box.

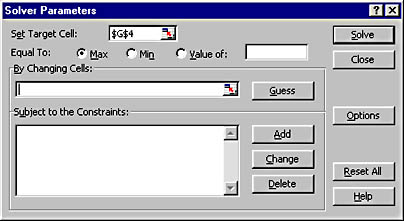
    4. In the following illustration, the three blank cells reserved for the number of coffee drinks in each category have been selected:

    click to view at full size.

    TIP
    Use the Guess Button to Preview the Result

    If you click the Guess button, the Solver will try to guess at the variable cells in your forecasting problem. The Solver creates the guess by looking at the cells referenced in the target cell formula. Don't rely on this guess— it will often be incorrect!

  • Constraints aren't required in all Solver problems, but this problem has three. Click the Add button to add the first constraint in the Add Constraint dialog box, which is shown here:

  • The first constraint is that you can sell only 500 cups of coffee in one week. To enter this constraint, click cell G8 (the cell containing the total cups formula), click <= in the operator drop-down list box, and type Max_cups in the Constraint text box (using the underline character to link the words). ( Max_cups is the name of cell G11 in our example.)

    • NOTE
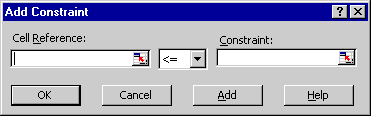
    You have the option of typing a value, clicking a cell, or entering a cell name in the Constraint text box. We entered a defined cell name because it makes the constraint easier to read and modify later.

  • Click the Add button to enter the first constraint and begin the second constraint— you can sell only 350 premium coffees in one week. With the insertion point in the Cell Reference text box, click cell G7 (the cell containing the premium cups formula), click <= in the operator drop-down list box, and type Max_premium (the name of cell G12) in the Constraint text box.

  • Click the Add button to enter the second constraint and begin the third constraint— you can sell only 125 caffè mochas in one week. Click cell D13 (the variable cell containing the number of mocha cups), click <= in the operator drop-down list box, and type Max_mocha (the name of cell G13) in the Constraint text box.

  • Click OK to add all three constraints to the Solver Parameters dialog box. It should look like the dialog box below.

    • click to view at full size.

    TIP
    To modify one of the constraints displayed in the Solver Parameters dialog box, select the constraint, and click Change. To customize the iteration and calculation parameters in the Solver utility, click Options and make your adjustments.

  • Your forecasting problem is ready to go, so click Solve to calculate the result.

    • After a few moments, the Solver displays a dialog box describing how the optimization analysis went. If the Solver ran into a problem, you'll see an error message, and you can click the Help button to learn more about the difficulty. If the Solver finds a solution, you'll see the following dialog box:

  • To display the new solution in your worksheet, click the Keep Solver Solution option button, and click OK. The Solver places an optimum value in the target cell and fills the variable cells with the best solutions that match the constraints you specified, as shown in Figure 23-4.

    • In this example, you've learned that if you're limited to selling 500 cups of coffee per week, you can expect a maximum of $918.75 in revenue, and your optimum drink distribution is 150 cups of regular coffee, 225 cups of caffè latte, and 125 cups of caffè mocha. Although this financial model doesn't consider several realistic business variables, such as the costs associated with running a shop and the benefits of making volume purchases, it does help you to forecast much more easily and quickly than you could using pencil and paper.

    click to view at full size.

    Figure 23-4. When the Solver finishes, it displays the values that produce the optimum result in the target cell.

    Editing Your Solver Forecast

    Perhaps the best feature of a Solver forecast is that you can easily edit it to evaluate new goals and contingencies. For example, if you decide that you want to earn exactly $700 per week from coffee drinks, you can use the Solver to tell you what the optimum combination of drinks would be. Setting a target value in the Solver is a little like using the Goal Seek command to determine an unknown variable, though you can use more than one variable.

    To edit your Solver forecast to find the variables to reach a specific goal, follow these steps:

    1. Choose Solver from the Tools menu. The Solver Parameters dialog box appears, still displaying the variables and constraints of your last Solver problem. You'll adjust these to compute a new forecasting goal.

    2. Click the Value Of option button and type 700 in the text box to the right. The Value Of option button sets the target cell to a particular goal so that you can determine the variable mix you need to reach your milestone. (In this example, the variable cells represent cups of coffee.) Your dialog box should look like this:

      3. click to view at full size.

    3. Click Solve to find a solution to your forecasting problem. When the Solver has finished, click OK to display the new solution in your worksheet.

    Figure 23-5 shows the solution the Solver generates if the variable cells are empty before you run the problem. (You can earn $700 by selling approximately 125 mochas, 151 lattes, and 94 regular coffees. The Solver calculates an exact answer, but because you can't sell partial cups of coffee, the variable cells are formatted to show integer— whole-number— values. Your actual revenue would be $700.75, and the subtotals would be slightly higher.)

    What If There Is More Than One Solution to the Problem?

    In the previous example, the Solver determined that you could sell 125 mochas, 151 lattes, and 94 regular coffees to reach your sales goal of $700. But you can also reach the $700 mark using a different product mix; for example, you could sell approximately 125 mochas and 210 lattes to reach $700. (Using this mix, your revenue would actually be $701.25.) So how did the Solver decide what the optimum product mix would be? Because you chose not to limit its options with constraints, the Solver simply started with the numbers in the variable cells and incremented them until it found an acceptable solution. For this reason, you can get different results from a nonlinear problem with multiple solutions if you use different starting values.

    click to view at full size.

    Figure 23-5. When you specify a target goal, the Solver computes an optimum product mix that meets your constraints.

    You can take advantage of the way the Solver reaches its results if there's a particular product mix that you'd like to use. Enter the values that you think might be acceptable in the variable cells before you run the Solver, and Excel will use those as starting values when it computes the solution. If you prefer to find a true optimal solution, you'll need to add extra constraints to the Solver Parameters dialog box before you run the forecast. For example, you might specify that a certain minimum must be met in each category, or that you'd like to minimize the number of products sold to reach your goal. You can have two constraints for each variable cell (an upper bounds and a lower bounds) to structure the computation and reach an optimal solution to your problem.


    Previous page
    Table of content
    Next page
    Running Microsoft Office 2000 Small Business
    Running Microsoft Office 2000
    ISBN: 1572319585
    EAN: 2147483647
    Year: 2005
    Pages: 228
    Authors: Michael Halvorson, Michael J. Young
    BUY ON AMAZON
    Lotus Notes and Domino 6 Development (2nd Edition)
    Software Configuration Management
    Cisco IP Telephony (CIPT) (Authorized Self-Study) (2nd Edition)
    Lean Six Sigma for Service : How to Use Lean Speed and Six Sigma Quality to Improve Services and Transactions
    GDI+ Programming with C#
    Microsoft Visual Basic .NET Programmers Cookbook (Pro-Developer)
    flylib.com © 2008-2017.
    If you may any questions please contact us: flylib@qtcs.net
    Privacy policy