Details
Inputting Frequency Counts
PROC FREQ can use either raw data or cell count data to produce frequency and crosstabulation tables. Raw data , also known as case-record data, report the data as one record for each subject or sample member. Cell count data report the data as a table, listing all possible combinations of data values along with the frequency counts. This way of presenting data often appears in published results.
The following DATA step statements store raw data in a SAS data set:
data Raw; input Subject $ R C @@; datalines; 01 1 1 02 1 1 03 1 1 04 1 1 05 1 1 06 1 2 07 1 2 08 1 2 09 2 1 10 2 1 11 2 1 12 2 1 13 2 2 14 2 2 14 2 2 ;
You can store the same data as cell counts using the following DATA step statements:
data CellCounts; input R C Count @@; datalines; 1 1 5 1 2 3 2 1 4 2 2 3 ;
The variable R contains the values for the rows, and the variable C contains the values for the columns . The Count variable contains the cell count for each row and column combination.
Both the Raw data set and the CellCounts data set produce identical frequency counts, two-way tables, and statistics. With the CellCounts data set, you must use a WEIGHT statement to specify that the Count variable contains cell counts. For example, to create a two-way crosstabulation table, submit the following statements:
proc freq data=CellCounts; weight Count; tables R*C; run;
Grouping with Formats
PROC FREQ groups a variable s values according to its formatted values. If you assign a format to a variable with a FORMAT statement, PROC FREQ formats the variable values before dividing observations into the levels of a frequency or crosstabulation table.
For example, suppose that a variable X has the values 1.1, 1.4, 1.7, 2.1, and 2.3. Each of these values appears as a level in the frequency table. If you decide to round each value to a single digit, include the following statement in the PROC FREQ step:
format X 1.;
Now the table lists the frequency count for formatted level 1 as two and formatted level 2 as three.
PROC FREQ treats formatted character variables in the same way. The formatted values are used to group the observations into the levels of a frequency table or crosstabulation table. PROC FREQ uses the entire value of a character format to classify an observation.
You can also use the FORMAT statement to assign formats that were created with the FORMAT procedure to the variables. User -written formats determine the number of levels for a variable and provide labels for a table. If you use the same data with different formats, then you can produce frequency counts and statistics for different classifications of the variable values.
When you use PROC FORMAT to create a user-written format that combines missing and nonmissing values into one category, PROC FREQ treats the entire category of formatted values as missing. For example, a questionnaire codes 1 as yes, 2 as no, and 8 as a no answer. The following PROC FORMAT step creates a user-written format:
proc format; value Questfmt 1 ='Yes' 2 ='No' 8,.='Missing'; run;
When you use a FORMAT statement to assign Questfmt . to a variable, the variable s frequency table no longer includes a frequency count for the response of 8. You must use the MISSING or MISSPRINT option in the TABLES statement to list the frequency for no answer. The frequency count for this level includes observations with either a value of 8 or a missing value (.).
The frequency or crosstabulation table lists the values of both character and numeric variables in ascending order based on internal (unformatted) variable values unless you change the order with the ORDER= option. To list the values in ascending order by formatted values, use ORDER=FORMATTED in the PROC FREQ statement.
For more information on the FORMAT statement, refer to SAS Language Reference: Concepts .
Missing Values
By default, PROC FREQ excludes missing values before it constructs the frequency and crosstabulation tables. PROC FREQ also excludes missing values before computing statistics. However, the total frequency of observations with missing values is displayed below each table. The following options change the way in which PROC FREQ handles missing values:
| MISSPRINT | includes missing value frequencies in frequency or crosstabulation tables. |
| MISSING | includes missing values in percentage and statistical calculations. |
The OUT= option in the TABLES statement includes an observation in the output data set that contains the frequency of missing values. The NMISS option in the OUTPUT statement creates a variable in the output data set that contains the number of missing values.
Figure 2.7 shows three ways in which PROC FREQ handles missing values. The first table uses the default method; the second table uses the MISSPRINT option; and the third table uses the MISSING option.
| |
*** Default *** The FREQ Procedure Cumulative Cumulative A Frequency Percent Frequency Percent ------------------------------------------------------ 1 2 50.00 2 50.00 2 2 50.00 4 100.00 Frequency Missing = 2 *** MISSPRINT Option *** The FREQ Procedure Cumulative Cumulative A Frequency Percent Frequency Percent ------------------------------------------------------ . 2 . . . 1 2 50.00 2 50.00 2 2 50.00 4 100.00 Frequency Missing = 2 *** MISSING Option *** The FREQ Procedure Cumulative Cumulative A Frequency Percent Frequency Percent ------------------------------------------------------ . 2 33.33 2 33.33 1 2 33.33 4 66.67 2 2 33.33 6 100.00
| |
Figure 2.7: Missing Values in Frequency Tables
When a combination of variable values for a crosstabulation is missing, PROC FREQ assigns zero to the frequency count for the table cell. By default, PROC FREQ omits missing combinations in list format and in the output data set that is created in a TABLES statement. To include the missing combinations, use the SPARSE option with the LIST or OUT= option in the TABLES statement.
PROC FREQ treats missing BY variable values like any other BY variable value. The missing values form a separate BY group. When the value of a WEIGHT variable is missing, PROC FREQ excludes the observation from the analysis.
Statistical Computations
Definitions and Notation
In this chapter, a two-way table represents the crosstabulation of variables X and Y . Let the rows of the table be labeled by the values X i , i = 1 , 2 , . . . , R , and the columns by Y j , j = 1 , 2 , . . . , C . Let n ij denote the cell frequency in the i th row and the j th column and define the following:

Scores
PROC FREQ uses scores for the variable values when computing the Mantel-Haenszel chi-square, Pearson correlation, Cochran-Armitage test for trend, weighted kappa coefficient, and Cochran-Mantel-Haenszel statistics. The SCORES= option in the TABLES statement specifies the score type that PROC FREQ uses. The available score types are TABLE, RANK, RIDIT, and MODRIDIT scores. The default score type is TABLE.
For numeric variables, table scores are the values of the row and column levels. If the row or column variables are formatted, then the table score is the internal numeric value corresponding to that level. If two or more numeric values are classified into the same formatted level, then the internal numeric value for that level is the smallest of these values. For character variables, table scores are defined as the row numbers and column numbers (that is, 1 for the first row, 2 for the second row, and so on).
Rank scores, which you can use to obtain nonparametric analyses, are defined by
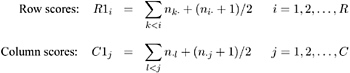
Note that rank scores yield midranks for tied values.
Ridit scores (Bross 1958; Mack and Skillings 1980) also yield nonparametric analyses, but they are standardized by the sample size . Ridit scores are derived from rank scores as
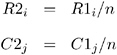
Modified ridit (MODRIDIT) scores (van Elteren 1960; Lehmann 1975), which also yield nonparametric analyses, represent the expected values of the order statistics for the uniform distribution on (0,1). Modified ridit scores are derived from rank scores as
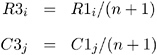
Chi-Square Tests and Statistics
When you specify the CHISQ option in the TABLES statement, PROC FREQ performs the following chi-square tests for each two-way table: Pearson chi-square, continuity-adjusted chi-square for 2 — 2 tables, likelihood -ratio chi-square, Mantel-Haenszel chi-square, and Fisher s exact test for 2 — 2 tables. Also, PROC FREQ computes the following statistics derived from the Pearson chi-square: the phi coefficient, the contingency coefficient, and Cramer s V . PROC FREQ computes Fisher s exact test for general R — C tables when you specify the FISHER (or EXACT) option in the TABLES statement, or, equivalently, when you specify the FISHER option in the EXACT statement.
For one-way frequency tables, PROC FREQ performs a chi-square goodness-of-fit test when you specify the CHISQ option. The other chi-square tests and statistics described in this section are defined only for two-way tables and so are not computed for one-way frequency tables.
All the two-way test statistics described in this section test the null hypothesis of no association between the row variable and the column variable. When the sample size n is large, these test statistics are distributed approximately as chi-square when the null hypothesis is true. When the sample size is not large, exact tests may be useful. PROC FREQ computes exact tests for the following chi-square statistics when you specify the corresponding option in the EXACT statement: Pearson chi-square, likelihood-ratio chi-square, and Mantel-Haenszel chi-square. See the section Exact Statistics beginning on page 142 for more information.
Note that the Mantel-Haenszel chi-square statistic is appropriate only when both variables lie on an ordinal scale. The other chi-square tests and statistics in this section are appropriate for either nominal or ordinal variables. The following sections give the formulas that PROC FREQ uses to compute the chi-square tests and statistics. For further information on the formulas and on the applicability of each statistic, refer to Agresti (1996), Stokes, Davis, and Koch (1995), and the other references cited for each statistic.
Chi-Square Test for One-Way Tables
For one-way frequency tables, the CHISQ option in the TABLES statement computes a chi-square goodness-of-fit test. Let C denote the number of classes, or levels, in the one-way table. Let f i denote the frequency of class i (or the number of observations in class i ) for i = 1 , 2 , ..., C . Then PROC FREQ computes the chi-square statistic as
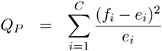
where e i is the expected frequency for class i under the null hypothesis.
In the test for equal proportions, which is the default for the CHISQ option, the null hypothesis specifies equal proportions of the total sample size for each class. Under this null hypothesis, the expected frequency for each class equals the total sample size divided by the number of classes,
In the test for specified frequencies, which PROC FREQ computes when you input null hypothesis frequencies using the TESTF= option, the expected frequencies are those TESTF= values. In the test for specified proportions, which PROC FREQ computes when you input null hypothesis proportions using the TESTP= option, the expected frequencies are determined from the TESTP= proportions p i , as
Under the null hypothesis (of equal proportions, specified frequencies, or specified proportions), this test statistic has an asymptotic chi-square distribution, with C ˆ’ 1 degrees of freedom. In addition to the asymptotic test, PROC FREQ computes the exact one-way chi-square test when you specify the CHISQ option in the EXACT statement.
Chi-Square Test for Two-Way Tables
The Pearson chi-square statistic for two-way tables involves the differences between the observed and expected frequencies, where the expected frequencies are computed under the null hypothesis of independence. The chi-square statistic is computed as
where
When the row and column variables are independent, Q P has an asymptotic chi-square distribution with ( R ˆ’ 1)( C ˆ’ 1) degrees of freedom. For large values of Q P , this test rejects the null hypothesis in favor of the alternative hypothesis of general association. In addition to the asymptotic test, PROC FREQ computes the exact chi-square test when you specify the PCHI or CHISQ option in the EXACT statement.
For a 2 — 2 table, the Pearson chi-square is also appropriate for testing the equality of two binomial proportions or, for R — 2 and 2 — C tables, the homogeneity of proportions. Refer to Fienberg (1980).
Likelihood-Ratio Chi-Square Test
The likelihood-ratio chi-square statistic involves the ratios between the observed and expected frequencies. The statistic is computed as
When the row and column variables are independent, G 2 has an asymptotic chi-square distribution with ( R ˆ’ 1)( C ˆ’ 1) degrees of freedom. In addition to the asymptotic test, PROC FREQ computes the exact test when you specify the LRCHI or CHISQ option in the EXACT statement.
Continuity-Adjusted Chi-Square Test
The continuity-adjusted chi-square statistic for 2 — 2 tables is similar to the Pearson chi-square, except that it is adjusted for the continuity of the chi-square distribution. The continuity-adjusted chi-square is most useful for small sample sizes. The use of the continuity adjustment is controversial ; this chi-square test is more conservative, and more like Fisher s exact test, when your sample size is small. As the sample size increases , the statistic becomes more and more like the Pearson chi-square.
The statistic is computed as
Under the null hypothesis of independence, Q C has an asymptotic chi-square distribution with ( R ˆ’ 1)( C ˆ’ 1) degrees of freedom.
Mantel-Haenszel Chi-Square Test
The Mantel-Haenszel chi-square statistic tests the alternative hypothesis that there is a linear association between the row variable and the column variable. Both variables must lie on an ordinal scale. The statistic is computed as
where r 2 is the Pearson correlation between the row variable and the column variable. For a description of the Pearson correlation, see the Pearson Correlation Coefficient section on page 113. The Pearson correlation and, thus, the Mantel-Haenszel chi-square statistic use the scores that you specify in the SCORES= option in the TABLES statement.
Under the null hypothesis of no association, Q MH has an asymptotic chi-square distribution with one degree of freedom. In addition to the asymptotic test, PROC FREQ computes the exact test when you specify the MHCHI or CHISQ option in the EXACT statement.
Refer to Mantel and Haenszel (1959) and Landis, Heyman, and Koch (1978).
Fisher s Exact Test
Fisher s exact test is another test of association between the row and column variables. This test assumes that the row and column totals are fixed, and then uses the hypergeometric distribution to compute probabilities of possible tables with these observed row and column totals. Fisher s exact test does not depend on any large-sample distribution assumptions, and so it is appropriate even for small sample sizes and for sparse tables.
2 — 2 Tables
For 2 — 2 tables, PROC FREQ gives the following information for Fisher s exact test: table probability, two-sided p -value, left-sided p -value, and right-sided p -value. The table probability equals the hypergeometric probability of the observed table, and is in fact the value of the test statistic for Fisher s exact test.
Where p is the hypergeometric probability of a specific table with the observed row and column totals, Fisher s exact p -values are computed by summing probabilities p over defined sets of tables,
The two-sided p -value is the sum of all possible table probabilties (for tables having the observed row and column totals) that are less than or equal to the observed table probability. So, for the two-sided p -value, the set A includes all possible tables with hypergeometric probabilities less than or equal to the probability of the observed table. A small two-sided p -value supports the alternative hypothesis of association between the row and column variables.
One-sided tests are defined in terms of the frequency of the cell in the first row and first column of the table, the (1,1) cell. Denoting the observed (1,1) cell frequency by F , the left-sided p -value for Fisher s exact test is probability that the (1,1) cell frequency is less than or equal to F . So, for the left-sided p -value, the set A includes those tables with a (1,1) cell frequency less than or equal to F . A small left-sided p -value supports the alternative hypothesis that the probability of an observation being in the first cell is less than expected under the null hypothesis of independent row and column variables.
Similarly, for a right-sided alternative hypothesis, A is the set of tables where the frequency of the (1,1) cell is greater than or equal to that in the observed table. A small right-sided p -value supports the alternative that the probability of the first cell is greater than that expected under the null hypothesis.
Because the (1,1) cell frequency completely determines the 2 — 2 table when the marginal row and column sums are fixed, these one-sided alternatives can be equivalently stated in terms of other cell probabilities or ratios of cell probabilities. The left-sided alternative is equivalent to an odds ratio greater than 1, where the odds ratio equals ( n 11 n 22 / n 12 n 21 ). Additionally, the left-sided alternative is equivalent to the column 1 risk for row 1 being less than the column 1 risk for row 2, p 11 < p 12 . Similarly, the right-sided alternative is equivalent to the column 1 risk for row 1 being greater than the column 1 risk for row 2, p 11 > p 12 . Refer to Agresti (1996).
R — C Tables
Fisher s exact test was extended to general R — C tables by Freeman and Halton (1951), and this test is also known as the Freeman-Halton test. For R — C tables, the two-sided p -value is defined the same as it is for 2 — 2 tables. The set A contains all tables with p less than or equal to the probability of the observed table. A small p -value supports the alternative hypothesis of association between the row and column variables. For R — C tables, Fisher s exact test is inherently two-sided. The alternative hypothesis is defined only in terms of general, and not linear, association. Therefore, PROC FREQ does not provide right-sided or left-sided p -values for general R — C tables.
For R — C tables, PROC FREQ computes Fisher s exact test using the network algorithm of Mehta and Patel (1983), which provides a faster and more efficient solution than direct enumeration. See the section Exact Statistics beginning on page 142 for more details.
Phi Coefficient
The phi coefficient is a measure of association derived from the Pearson chi-square statistic. It has the range ˆ’ 1 ‰ ![]() ‰ 1 for 2 — 2 tables. Otherwise , the range is
‰ 1 for 2 — 2 tables. Otherwise , the range is ![]() (Liebetrau 1983). The phi coefficient is computed as
(Liebetrau 1983). The phi coefficient is computed as
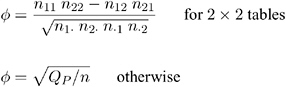
Refer to Fleiss (1981, pp. 59 “60).
Contingency Coefficient
The contingency coefficient is a measure of association derived from the Pearson chi-square. It has the range ![]() , where m = min ( R, C ) (Liebetrau 1983). The contingency coefficient is computed as
, where m = min ( R, C ) (Liebetrau 1983). The contingency coefficient is computed as

Refer to Kendall and Stuart (1979, pp. 587 “588).
Cramer s V
Cramer s V is a measure of association derived from the Pearson chi-square. It is designed so that the attainable upper bound is always 1. It has the range ˆ’ 1 ‰ V ‰ 1 for 2 — 2 tables; otherwise, the range is 0 ‰ V ‰ 1. Cramer s V is computed as
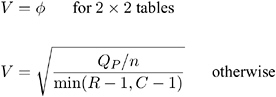
Refer to Kendall and Stuart (1979, p. 588).
Measures of Association
When you specify the MEASURES option in the TABLES statement, PROC FREQ computes several statistics that describe the association between the two variables of the contingency table. The following are measures of ordinal association that consider whether the variable Y tends to increase as X increases: gamma, Kendall s tau- b , Stuart s tau- c , and Somers D . These measures are appropriate for ordinal variables, and they classify pairs of observations as concordant or discordant . A pair is concordant if the observation with the larger value of X also has the larger value of Y . A pair is discordant if the observation with the larger value of X has the smaller value of Y . Refer to Agresti (1996) and the other references cited in the discussion of each measure of association.
The Pearson correlation coefficient and the Spearman rank correlation coefficient are also appropriate for ordinal variables. The Pearson correlation describes the strength of the linear association between the row and column variables, and it is computed using the row and column scores specified by the SCORES= option in the TABLES statement. The Spearman correlation is computed with rank scores. The polychoric correlation ( requested by the PLCORR option) also requires ordinal variables and assumes that the variables have an underlying bivariate normal distribution. The following measures of association do not require ordinal variables, but they are appropriate for nominal variables: lambda asymmetric, lambda symmetric, and uncertainty coefficients.
PROC FREQ computes estimates of the measures according to the formulas given in the discussion of each measure of association. For each measure, PROC FREQ computes an asymptotic standard error (ASE), which is the square root of the asymptotic variance denoted by var in the following sections.
Confidence Limits
If you specify the CL option in the TABLES statement, PROC FREQ computes asymptotic confidence limits for all MEASURES statistics. The confidence coefficient is determined according to the value of the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
The confidence limits are computed as
where est is the estimate of the measure, z ± / 2 is the 100(1 ˆ’ ± /2) percentile of the standard normal distribution, and ASE is the asymptotic standard error of the estimate.
Asymptotic Tests
For each measure that you specify in the TEST statement, PROC FREQ computes an asymptotic test of the null hypothesis that the measure equals zero. Asymptotic tests are available for the following measures of association: gamma, Kendall s tau- b , Stuart s tau- c , Somers D ( R C ), Somers D ( C R ), the Pearson correlation coefficient, and the Spearman rank correlation coefficient. To compute an asymptotic test, PROC FREQ uses a standardized test statistic z , which has an asymptotic standard normal distribution under the null hypothesis. The standardized test statistic is computed as
where est is the estimate of the measure and var ( est ) is the variance of the estimate under the null hypothesis. Formulas for var ( est ) are given in the discussion of each measure of association.
Note that the ratio of est to ![]() is the same for the following measures: gamma, Kendall s tau- b , Stuart s tau- c , Somers D ( R C ), and Somers D ( C R ). Therefore, the tests for these measures are identical. For example, the p -values for the test of H : gamma = 0 equal the p -values for the test of H : tau- b = 0.
is the same for the following measures: gamma, Kendall s tau- b , Stuart s tau- c , Somers D ( R C ), and Somers D ( C R ). Therefore, the tests for these measures are identical. For example, the p -values for the test of H : gamma = 0 equal the p -values for the test of H : tau- b = 0.
PROC FREQ computes one-sided and two-sided p -values for each of these tests. When the test statistic z is greater than its null hypothesis expected value of zero, PROC FREQ computes the right-sided p -value, which is the probability of a larger value of the statistic occurring under the null hypothesis. A small right-sided p -value supports the alternative hypothesis that the true value of the measure is greater than zero. When the test statistic is less than or equal to zero, PROC FREQ computes the left-sided p -value, which is the probability of a smaller value of the statistic occurring under the null hypothesis. A small left-sided p -value supports the alternative hypothesis that the true value of the measure is less than zero. The one-sided p -value P 1 can be expressed as
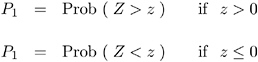
where Z has a standard normal distribution. The two-sided p -value P 2 is computed as
Exact Tests
Exact tests are available for two measures of association, the Pearson correlation coefficient and the Spearman rank correlation coefficient. If you specify the PCORR option in the EXACT statement, PROC FREQ computes the exact test of the hypothesis that the Pearson correlation equals zero. If you specify the SCORR option in the EXACT statement, PROC FREQ computes the exact test of the hypothesis that the Spearman correlation equals zero. See the section Exact Statistics beginning on page 142 for information on exact tests.
Gamma
The estimator of gamma is based only on the number of concordant and discordant pairs of observations. It ignores tied pairs (that is, pairs of observations that have equal values of X or equal values of Y ). Gamma is appropriate only when both variables lie on an ordinal scale. It has the range ˆ’ 1 ‰ “ ‰ 1. If the two variables are independent, then the estimator of gamma tends to be close to zero. Gamma is estimated by
with asymptotic variance
The variance of the estimator under the null hypothesis that gamma equals zero is computed as
For 2 — 2 tables, gamma is equivalent to Yule s Q . Refer to Goodman and Kruskal (1979), Agresti (1990), and Brown and Benedetti (1977).
Kendall s Tau-b
Kendall s tau- b is similar to gamma except that tau- b uses a correction for ties. Tau- b is appropriate only when both variables lie on an ordinal scale. Tau- b has the range ˆ’ 1 ‰ b ‰ 1. It is estimated by
with

where
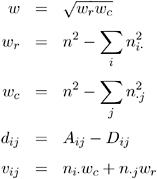
The variance of the estimator under the null hypothesis that tau- b equals zero is computed as

Refer to Kendall (1955) and Brown and Benedetti (1977).
Stuart s Tau-c
Stuart s tau- c makes an adjustment for table size in addition to a correction for ties. Tau- c is appropriate only when both variables lie on an ordinal scale. Tau- c has the range ˆ’ 1 ‰ c ‰ 1. It is estimated by
with

where
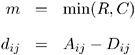
The variance of the estimator under the null hypothesis that tau- c equals zero is
Refer to Brown and Benedetti (1977).
Somers D (CR) and D (RC)
Somers D ( C R ) and Somers D ( R C ) are asymmetric modifications of tau- b . C R denotes that the row variable X is regarded as an independent variable, while the column variable Y is regarded as dependent. Similarly, R C denotes that the column variable Y is regarded as an independent variable, while the row variable X is regarded as dependent. Somers D differs from tau- b in that it uses a correction only for pairs that are tied on the independent variable. Somers D is appropriate only when both variables lie on an ordinal scale. It has the range ˆ’ 1 ‰ D ‰ 1. Formulas for Somers D ( R C ) are obtained by interchanging the indices.
with
where
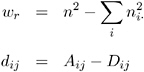
The variance of the estimator under the null hypothesis that D ( C R ) equals zero is computed as
Refer to Somers (1962), Goodman and Kruskal (1979), and Liebetrau (1983).
Pearson Correlation Coefficient
PROC FREQ computes the Pearson correlation coefficient using the scores specified in the SCORES= option. The Pearson correlation is appropriate only when both variables lie on an ordinal scale. It has the range ˆ’ 1 ‰ ‰ 1. The Pearson correlation coefficient is computed as
with
The row scores R i and the column scores C j are determined by the SCORES= option in the TABLES statement, and
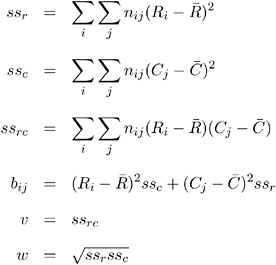
Refer to Snedecor and Cochran (1989) and Brown and Benedetti (1977).
To compute an asymptotic test for the Pearson correlation, PROC FREQ uses a standardized test statistic r *, which has an asymptotic standard normal distribution under the null hypothesis that the correlation equals zero. The standardized test statistic is computed as
where var ( r ) is the variance of the correlation under the null hypothesis.
The asymptotic variance is derived for multinomial sampling in a contingency table framework, and it differs from the form obtained under the assumption that both variables are continuous and normally distributed. Refer to Brown and Benedetti (1977).
PROC FREQ also computes the exact test for the hypothesis that the Pearson correlation equals zero when you specify the PCORR option in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
Spearman Rank Correlation Coefficient
The Spearman correlation coefficient is computed using rank scores R 1 i and C 1 j , defined in the section Scores beginning on page 102. It is appropriate only when both variables lie on an ordinal scale. It has the range ˆ’ 1 ‰ s ‰ 1. The Spearman correlation coefficient is computed as
with
where
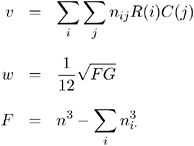
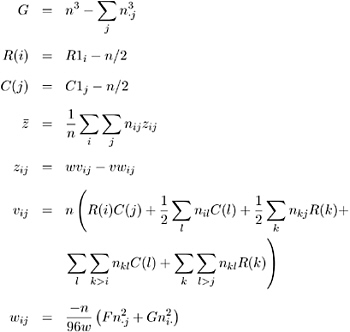
Refer to Snedecor and Cochran (1989) and Brown and Benedetti (1977).
To compute an asymptotic test for the Spearman correlation, PROC FREQ uses a standardized test statistic ![]() , which has an asymptotic standard normal distribution under the null hypothesis that the correlation equals zero. The standardized test statistic is computed as
, which has an asymptotic standard normal distribution under the null hypothesis that the correlation equals zero. The standardized test statistic is computed as
where var ( r s ) is the variance of the correlation under the null hypothesis.
where
The asymptotic variance is derived for multinomial sampling in a contingency table framework, and it differs from the form obtained under the assumption that both variables are continuous and normally distributed. Refer to Brown and Benedetti (1977).
PROC FREQ also computes the exact test for the hypothesis that the Spearman rank correlation equals zero when you specify the SCORR option in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
Polychoric Correlation
When you specify the PLCORR option in the TABLES statement, PROC FREQ computes the polychoric correlation. This measure of association is based on the assumption that the ordered, categorical variables of the frequency table have an underlying bivariate normal distribution. For 2 — 2 tables, the polychoric correlation is also known as the tetrachoric correlation. Refer to Drasgow (1986) for an overview of polychoric correlation. The polychoric correlation coefficient is the maximum likelihood estimate of the product-moment correlation between the normal variables, estimating thresholds from the observed table frequencies. The range of the polychoric correlation is from ˆ’ 1 to 1. Olsson (1979) gives the likelihood equations and an asymptotic covariance matrix for the estimates.
To estimate the polychoric correlation, PROC FREQ iteratively solves the likelihood equations by a Newton-Raphson algorithm using the Pearson correlation coefficient as the initial approximation . Iteration stops when the convergence measure falls below the convergence criterion or when the maximum number of iterations is reached, whichever occurs first. The CONVERGE= option sets the convergence criterion, and the default value is 0.0001. The MAXITER= option sets the maximum number of iterations, and the default value is 20.
Lambda Asymmetric
Asymmetric lambda, » ( C R ), is interpreted as the probable improvement in predicting the column variable Y given knowledge of the row variable X . Asymmetric lambda has the range 0 ‰ » ( C R ) ‰ 1. It is computed as
with
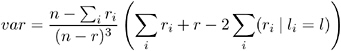
where
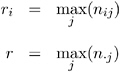
Also, let l i be the unique value of j such that r i = n ij , and let l be the unique value of j such that r = n . j .
Because of the uniqueness assumptions, ties in the frequencies or in the marginal totals must be broken in an arbitrary but consistent manner. In case of ties, l is defined here as the smallest value of j such that r = n. j . For a given i , if there is at least one value j such that n ij = r i = c j , then l i is defined here to be the smallest such value of j . Otherwise, if n il = r i , then l i is defined to be equal to l . If neither condition is true, then l i is taken to be the smallest value of j such that n ij = r i . The formulas for lambda asymmetric ( R C ) can be obtained by interchanging the indices.
Refer to Goodman and Kruskal (1979).
Lambda Symmetric
The nondirectional lambda is the average of the two asymmetric lambdas, ( C R ) and » ( R C ). Lambda symmetric has the range 0 ‰ » ‰ 1. Lambda symmetric is defined as
with
where

Refer to Goodman and Kruskal (1979).
Uncertainty Coefficients (CR) and (RC)
The uncertainty coefficient, U ( C R ), is the proportion of uncertainty (entropy) in the column variable Y that is explained by the row variable X . It has the range 0 ‰ U ( C R ) ‰ 1. The formulas for U ( R C ) can be obtained by interchanging the indices.
with
where
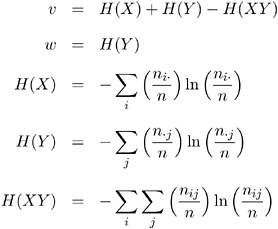
Refer to Theil (1972, pp. 115 “120) and Goodman and Kruskal (1979).
Uncertainty Coefficient (U)
The uncertainty coefficient, U , is the symmetric version of the two asymmetric coefficients. It has the range 0 ‰ U ‰ 1. It is defined as
with
Refer to Goodman and Kruskal (1979).
Binomial Proportion
When you specify the BINOMIAL option in the TABLES statement, PROC FREQ computes a binomial proportion for one-way tables. By default this is the proportion of observations in the first variable level, or class, that appears in the output. To specify a different level, use the LEVEL= option.
where n 1 is the frequency for the first level and n is the total frequency for the one-way table. The standard error for the binomial proportion is computed as
Using the normal approximation to the binomial distribution, PROC FREQ constructs asymptotic confidence limits for p according to
where z ± / 2 is the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution. The confidence level is determined by the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
If you specify the BINOMIALC option, PROC FREQ includes a continuity correction of 1 / 2 n in the asymptotic confidence limits for p . The purpose of this correction is to adjust for the difference between the normal approximation and the binomial distribution, which is a discrete distribution. Refer to Fleiss (1981). With the continuity correction, the asymptotic confidence limits for p are
Additionally, PROC FREQ computes exact confidence limits for the binomial proportion using the F distribution method given in Collett (1991) and also described by Leemis and Trivedi (1996).
PROC FREQ computes an asymptotic test of the hypothesis that the binomial proportion equals p , where the value of p is specified by the P= option in the TABLES statement. If you do not specify a value for the P= option, PROC FREQ uses p = 0 . 5 by default. The asymptotic test statistic is
If you specify the BINOMIALC option, PROC FREQ includes a continuity correction in the asymptotic test statistic, towards adjusting for the difference between the normal approximation and the discrete binomial distribution. Refer to Fleiss (1981). The continuity correction of (1 / 2 n ) is subtracted from ( ![]() ˆ’ p ) in the numerator of the test statistic z if (
ˆ’ p ) in the numerator of the test statistic z if ( ![]() ˆ’ p ) is positive; otherwise, the continuity correction is added to the numerator.
ˆ’ p ) is positive; otherwise, the continuity correction is added to the numerator.
PROC FREQ computes one-sided and two-sided p -values for this test. When the test statistic z is greater than zero, its expected value under the null hypothesis, PROC FREQ computes the right-sided p -value, which is the probability of a larger value of the statistic occurring under the null hypothesis. A small right-sided p -value supports the alternative hypothesis that the true value of the proportion is greater than p . When the test statistic is less than or equal to zero, PROC FREQ computes the left-sided p -value, which is the probability of a smaller value of the statistic occurring under the null hypothesis. A small left-sided p -value supports the alternative hypothesis that the true value of the proportion is less than p . The one-sided p -value P 1 can be expressed as
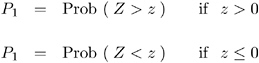
where Z has a standard normal distribution. The two-sided p -value P 2 is computed as
When you specify the BINOMIAL option in the EXACT statement, PROC FREQ also computes an exact test of the null hypothesis H : p = p . To compute this exact test, PROC FREQ uses the binomial probability function
where the variable X has a binomial distribution with parameters n and p . To compute Prob( X ‰ n 1 ), PROC FREQ sums these binomial probabilities over x from zero to n 1 . To compute Prob( X ‰ n 1 ), PROC FREQ sums these binomial probabilities over x from n 1 to n . Then the exact one-sided p -value is
and the exact two-sided p -value is
Risks and Risk Differences
The RISKDIFF option in the TABLES statement provides estimates of risks (or binomial proportions) and risk differences for 2 —2 tables. This analysis may be appropriate when comparing the proportion of some characteristic for two groups, where row 1 and row 2 correspond to the two groups, and the columns correspond to two possible characteristics or outcomes . For example, the row variable might be a treatment or dose, and the column variable might be the response. Refer to Collett (1991), Fleiss (1981), and Stokes, Davis, and Koch (1995).
Let the frequencies of the 2 —2 table be represented as follows .
| Column 1 | Column 2 | Total | |
|---|---|---|---|
| Row 1 | n 11 | n 12 | n 1 . |
| Row 2 | n 21 | n 22 | n 2 . |
| Total | n. 1 | n. 2 | n |
The column 1 risk for row 1 is the proportion of row 1 observations classified in column 1,
This estimates the conditional probability of the column 1 response, given the first level of the row variable.
The column 1 risk for row 2 is the proportion of row 2 observations classified in column 1,
and the overall column 1 risk is the proportion of all observations classified in column 1,
The column 1 risk difference compares the risks for the two rows, and it is computed as the column 1 risk for row 1 minus the column 1 risk for row 2,
The risks and risk difference are defined similarly for column 2.
The standard error of the column 1 risk estimate for row i is computed as
The standard error of the overall column 1 risk estimate is computed as
If the two rows represent independent binomial samples, the standard error for the column 1 risk difference is computed as
The standard errors are computed in a similar manner for the column 2 risks and risk difference.
Using the normal approximation to the binomial distribution, PROC FREQ constructs asymptotic confidence limits for the risks and risk differences according to
where est is the estimate, z ± / 2 is the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution, and se ( est ) is the standard error of the estimate. The confidence level ± is determined from the value of the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
If you specify the RISKDIFFC option, PROC FREQ includes continuity corrections in the asymptotic confidence limits for the risks and risk differences. Continuity corrections adjust for the difference between the normal approximation and the discrete binomial distribution. Refer to Fleiss (1981). Including a continuity correction, the asymptotic confidence limits become
where cc is the continuity correction. For the column 1 risk for row 1, cc = (1 / 2 n 1. ); for the column 1 risk for row 2, cc = (1 / 2 n 2 .); for the overall column 1 risk, cc = (1 / 2 n ); and for the column 1 risk difference, cc = ((1 /n 1. + 1 /n 2 .) / 2). Continuity corrections are computed similarly for the column 2 risks and risk difference.
PROC FREQ computes exact confidence limits for the column 1, column 2, and overall risks using the F distribution method given in Collett (1991) and also described by Leemis and Trivedi (1996). PROC FREQ does not provide exact confidence limits for the risk differences. Refer to Agresti (1992) for a discussion of issues involved in constructing exact confidence limits for differences of proportions.
Odds Ratio and Relative Risks for 2 x 2 Tables
Odds Ratio (Case-Control Studies)
The odds ratio is a useful measure of association for a variety of study designs. For a retrospective design called a case-control study , the odds ratio can be used to estimate the relative risk when the probability of positive response is small (Agresti 1990). In a case-control study, two independent samples are identified based on a binary (yes-no) response variable, and the conditional distribution of a binary explanatory variable is examined, within fixed levels of the response variable. Refer to Stokes, Davis, and Koch (1995) and Agresti (1996).
The odds of a positive response (column 1) in row 1 is n 11 /n 12 . Similarly, the odds of a positive response in row 2 is n 21 /n 22 . The odds ratio is formed as the ratio of the row 1 odds to the row 2 odds. The odds ratio for 2 —2 tables is defined as
The odds ratio can be any nonnegative number. When the row and column variables are independent, the true value of the odds ratio equals 1. An odds ratio greater than 1 indicates that the odds of a positive response are higher in row 1 than in row 2. Values less than 1 indicate the odds of positive response are higher in row 2. The strength of association increases with the deviation from 1.
The transformation G = (OR ˆ’ 1) / (OR + 1) transforms the odds ratio to the range ( ˆ’ 1 , 1) with G = 0 when OR = 1; G = ˆ’ 1 when OR = 0; and G approaches 1 as OR approaches infinity. G is the gamma statistic, which PROC FREQ computes when you specify the MEASURES option.
The asymptotic 100(1 ˆ’ ± )% confidence limits for the odds ratio are
where
and z is the 100(1 ˆ’ ± /2) percentile of the standard normal distribution. If any of the four cell frequencies are zero, the estimates are not computed.
When you specify option OR in the EXACT statement, PROC FREQ computes exact confidence limits for the odds ratio. Because this is a discrete problem, the confidence coefficient for these exact confidence limits is not exactly 1 ˆ’ ± but is at least 1 ˆ’ ± . Thus, these confidence limits are conservative. Refer to Agresti (1992).
PROC FREQ computes exact confidence limits for the odds ratio with an algorithm based on that presented by Thomas (1971). Refer also to Gart (1971). The following two equations are solved iteratively for the lower and upper confidence limits, ![]() 1 and
1 and ![]() 2 .
2 .
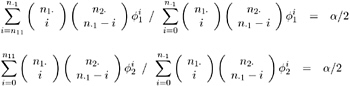
When the odds ratio equals zero, which occurs when either n 11 = 0 or n 22 = 0, then PROC FREQ sets the lower exact confidence limit to zero and determines the upper limit with level ± . Similarly, when the odds ratio equals infinity, which occurs when either n 12 = 0 or n 21 = 0, then PROC FREQ sets the upper exact confidence limit to infinity and determines the lower limit with level ± .
Relative Risks (Cohort Studies)
These measures of relative risk are useful in cohort ( prospective ) study designs, where two samples are identified based on the presence or absence of an explanatory factor. The two samples are observed in future time for the binary (yes-no) response variable under study. Relative risk measures are also useful in cross-sectional studies, where two variable are observed simultaneously . Refer to Stokes, Davis, and Koch (1995) and Agresti (1996).
The column 1 relative risk is the ratio of the column 1 risks for row 1 to row 2. The column 1 risk for row 1 is the proportion of the row 1 observations classified in column 1,
Similarly, the column 1 risk for row 2 is
The column 1 relative risk is then computed as
A relative risk greater than 1 indicates that the probability of positive response is greater in row 1 than in row 2. Similarly, a relative risk less than 1 indicates that the probability of positive response is less in row 1 than in row 2. The strength of association increases with the deviation from 1.
The asymptotic 100(1 ˆ’ ± )% confidence limits for the column 1 relative risk are
where
and z is the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution. If either n 11 or n 21 is zero, the estimates are not computed.
PROC FREQ computes the column 2 relative risks in a similar manner.
Cochran-Armitage Test for Trend
The TREND option in the TABLES statement requests the Cochran-Armitage test for trend, which tests for trend in binomial proportions across levels of a single factor or covariate. This test is appropriate for a contingency table where one variable has two levels and the other variable is ordinal. The two-level variable represents the response, and the other variable represents an explanatory variable with ordered levels. When the contingency table has two columns and R rows, PROC FREQ tests for trend across the R levels of the row variable, and the binomial proportion is computed as the proportion of observations in the first column. When the table has two rows and C columns, PROC FREQ tests for trend across the C levels of the column variable, and the binomial proportion is computed as the proportion of observations in the first row.
The trend test is based upon the regression coefficient for the weighted linear regression of the binomial proportions on the scores of the levels of the explanatory variable. Refer to Margolin (1988) and Agresti (1990). If the contingency table has two columns and R rows, the trend test statistic is computed as
where
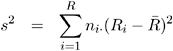
The row scores R i are determined by the value of the SCORES= option in the TABLES statement. By default, PROC FREQ uses table scores. For character variables, the table scores for the row variable are the row numbers (for example, 1 for the first row, 2 for the second row, and so on). For numeric variables, the table score for each row is the numeric value of the row level. When you perform the trend test, the explanatory variable may be numeric (for example, dose of a test substance), and these variable values may be appropriate scores. If the explanatory variable has ordinal levels that are not numeric, you can assign meaningful scores to the variable levels. Sometimes equidistant scores, such as the table scores for a character variable, may be appropriate. For more information on choosing scores for the trend test, refer to Margolin (1988).
The null hypothesis for the Cochran-Armitage test is no trend, which means that the binomial proportion p i 1 = n i 1 /n i. is the same for all levels of the explanatory variable. Under this null hypothesis, the trend test statistic is asymptotically distributed as a standard normal random variable. In addition to this asymptotic test, PROC FREQ can compute the exact trend test, which you request by specifying the TREND option in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
PROC FREQ computes one-sided and two-sided p -values for the trend test. When the test statistic is greater than its null hypothesis expected value of zero, PROC FREQ computes the right-sided p -value, which is the probability of a larger value of the statistic occurring under the null hypothesis. A small right-sided p -value supports the alternative hypothesis of increasing trend in binomial proportions from row 1 to row R . When the test statistic is less than or equal to zero, PROC FREQ outputs the left-sided p -value. A small left-sided p -value supports the alternative of decreasing trend.
The one-sided p -value P 1 can be expressed as
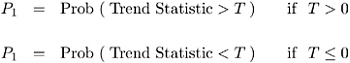
The two-sided p -value P 2 is computed as
Jonckheere-Terpstra Test
The JT option in the TABLES statement requests the Jonckheere-Terpstra test, which is a nonparametric test for ordered differences among classes. It tests the null hypothesis that the distribution of the response variable does not differ among classes. It is designed to detect alternatives of ordered class differences, which can be expressed as 1 ‰ 2 ‰ ‰ R (or 1 ‰ 2 ‰ ‰ R ), with at least one of the inequalities being strict, where i denotes the effect of class i . For such ordered alternatives, the Jonckheere-Terpstra test can be preferable to tests of more general class difference alternatives, such as the Kruskal “Wallis test (requested by the option WILCOXON in the NPAR1WAY procedure). Refer to Pirie (1983) and Hollander and Wolfe (1973) for more information about the Jonckheere-Terpstra test.
The Jonckheere-Terpstra test is appropriate for a contingency table in which an ordinal column variable represents the response. The row variable, which can be nominal or ordinal, represents the classification variable. The levels of the row variable should be ordered according to the ordering you want the test to detect. The order of variable levels is determined by the ORDER= option in the PROC FREQ statement. The default is ORDER=INTERNAL, which orders by unformatted values. If you specify ORDER=DATA, PROC FREQ orders values according to their order in the input data set. For more information on how to order variable levels, see the ORDER= option on page 76.
The Jonckheere-Terpstra test statistic is computed by first forming R ( R ˆ’ 1) / 2 Mann-Whitney counts M i,i ² , where i<i ² , for pairs of rows in the contingency table,
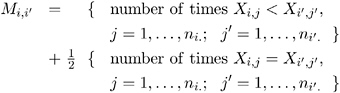
where X i,j is response j in row i . Then the Jonckheere-Terpstra test statistic is computed as
This test rejects the null hypothesis of no difference among classes for large values of J . Asymptotic p -values for the Jonckheere-Terpstra test are obtained by using the normal approximation for the distribution of the standardized test statistic. The standardized test statistic is computed as
where E ( J ) and var ( J ) are the expected value and variance of the test statistic under the null hypothesis.
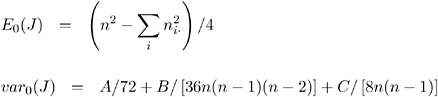
where
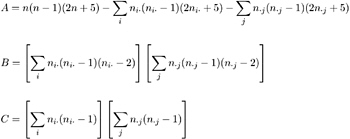
In addition to this asymptotic test, PROC FREQ can compute the exact Jonckheere-Terpstra test, which you request by specifying the JT option in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
PROC FREQ computes one-sided and two-sided p -values for the Jonckheere-Terpstra test. When the standardized test statistic is greater than its null hypothesis expected value of zero, PROC FREQ computes the right-sided p -value, which is the probability of a larger value of the statistic occurring under the null hypothesis. A small right-sided p -value supports the alternative hypothesis of increasing order from row 1 to row R . When the standardized test statistic is less than or equal to zero, PROC FREQ computes the left-sided p -value. A small left-sided p -value supports the alternative of decreasing order from row 1 to row R .
The one-sided p -value P 1 can be expressed as

The two-sided p -value P 2 is computed as
Tests and Measures of Agreement
When you specify the AGREE option in the TABLES statement, PROC FREQ computes tests and measures of agreement for square tables (that is, for tables where the number of rows equals the number of columns). For two-way tables, these tests and measures include McNemar s test for 2 —2 tables, Bowker s test of symmetry, the simple kappa coefficient, and the weighted kappa coefficient. For multiple strata ( n -way tables, where n > 2), PROC FREQ computes the overall simple kappa coefficient and the overall weighted kappa coefficient, as well as tests for equal kappas (simple and weighted) among strata. Cochran s Q is computed for multi-way tables when each variable has two levels, that is, for 2 —2 — —2 tables.
PROC FREQ computes the kappa coefficients (simple and weighted), their asymptotic standard errors, and their confidence limits when you specify the AGREE option in the TABLES statement. If you also specify the KAPPA option in the TEST statement, then PROC FREQ computes the asymptotic test of the hypothesis that simple kappa equals zero. Similarly, if you specify the WTKAP option in the TEST statement, PROC FREQ computes the asymptotic test for weighted kappa.
In addition to the asymptotic tests described in this section, PROC FREQ computes the exact p -value for McNemar s test when you specify the option MCNEM in the EXACT statement. For the kappa statistics, PROC FREQ computes the exact test of the hypothesis that kappa (or weighted kappa) equals zero when you specify the option KAPPA (or WTKAP) in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
The discussion of each test and measures of agreement provides the formulas that PROC FREQ uses to compute the AGREE statistics. For information on the use and interpretation of these statistics, refer to Agresti (1990), Agresti (1996), Fleiss (1981), and the other references cited for each statistic.
McNemar s Test
PROC FREQ computes McNemar s test for 2 —2 tables when you specify the AGREE option. McNemar s test is appropriate when you are analyzing data from matched pairs of subjects with a dichotomous (yes-no) response. It tests the null hypothesis of marginal homogeneity, or p 1. = p . 1 . McNemar s test is computed as
Under the null hypothesis, Q M has an asymptotic chi-square distribution with one degree of freedom. Refer to McNemar (1947), as well as the references cited in the preceding section. In addition to the asymptotic test, PROC FREQ also computes the exact p -value for McNemar s test when you specify the MCNEM option in the EXACT statement.
Bowker s Test of Symmetry
For Bowker s test of symmetry, the null hypothesis is that the probabilities in the square table satisfy symmetry or that p ij = p ji for all pairs of table cells . When there are more than two categories, Bowker s test of symmetry is calculated as
For large samples, Q B has an asymptotic chi-square distribution with R ( R ˆ’ 1) / 2 degrees of freedom under the null hypothesis of symmetry of the expected counts. Refer to Bowker (1948). For two categories, this test of symmetry is identical to McNemar s test.
Simple Kappa Coefficient
The simple kappa coefficient, introduced by Cohen (1960), is a measure of interrater agreement:
where P o = & pound ; i p ii and P e = i p i. p .i . If the two response variables are viewed as two independent ratings of the n subjects, the kappa coefficient equals +1 when there is complete agreement of the raters. When the observed agreement exceeds chance agreement, kappa is positive, with its magnitude reflecting the strength of agreement. Although this is unusual in practice, kappa is negative when the observed agreement is less than chance agreement. The minimum value of kappa is between ˆ’ 1 and 0, depending on the marginal proportions.
The asymptotic variance of the simple kappa coefficient can be estimated by the following, according to Fleiss, Cohen, and Everitt (1969):
where
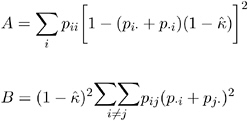
and
PROC FREQ computes confidence limits for the simple kappa coefficient according to
where z ± / 2 is the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution. The value of ± is determined by the value of the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
To compute an asymptotic test for the kappa coefficient, PROC FREQ uses a standardized test statistic ![]() *, which has an asymptotic standard normal distribution under the null hypothesis that kappa equals zero. The standardized test statistic is computed as
*, which has an asymptotic standard normal distribution under the null hypothesis that kappa equals zero. The standardized test statistic is computed as
where var ( ![]() ) is the variance of the kappa coefficient under the null hypothesis.
) is the variance of the kappa coefficient under the null hypothesis.
Refer to Fleiss (1981).
In addition to the asymptotic test for kappa, PROC FREQ computes the exact test when you specify the KAPPA or AGREE option in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
Weighted Kappa Coefficient
The weighted kappa coefficient is a generalization of the simple kappa coefficient, using weights to quantify the relative difference between categories. For 2 —2 tables, the weighted kappa coefficient equals the simple kappa coefficient. PROC FREQ displays the weighted kappa coefficient only for tables larger than 2 —2. PROC FREQ computes the weights from the column scores, using either the Cicchetti-Allison weight type or the Fleiss-Cohen weight type, both of which are described in the following section. The weights w ij are constructed so that 0 ‰ w ij < 1 for all i ‰ j , w ii = 1 for all i , and w ij = w ji . The weighted kappa coefficient is defined as
where
and
The asymptotic variance of the weighted kappa coefficient can be estimated by the following, according to Fleiss, Cohen, and Everitt (1969):
where
and
PROC FREQ computes confidence limits for the weighted kappa coefficient according to
where z ± / 2 is the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution. The value of is determined by the value of the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
To compute an asymptotic test for the weighted kappa coefficient, PROC FREQ uses a standardized test statistic ![]() , which has an asymptotic standard normal distribution under the null hypothesis that weighted kappa equals zero. The standardized test statistic is computed as
, which has an asymptotic standard normal distribution under the null hypothesis that weighted kappa equals zero. The standardized test statistic is computed as
where var ( ![]() w ) is the variance of the weighted kappa coefficient under the null hypothesis.
w ) is the variance of the weighted kappa coefficient under the null hypothesis.
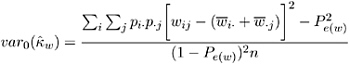
Refer to Fleiss (1981).
In addition to the asymptotic test for weighted kappa, PROC FREQ computes the exact test when you specify the WTKAP or AGREE option in the EXACT statement. See the section Exact Statistics beginning on page 142 for information on exact tests.
Weights
PROC FREQ computes kappa coefficient weights using the column scores and one of two available weight types. The column scores are determined by the SCORES= option in the TABLES statement. The two available weight types are Cicchetti-Allison and Fleiss-Cohen, and PROC FREQ uses the Cicchetti-Allison type by default. If you specify (WT=FC) with the AGREE option, then PROC FREQ uses the Fleiss-Cohen weight type to construct kappa weights.
PROC FREQ computes Cicchetti-Allison kappa coefficient weights using a form similar to that given by Cicchetti and Allison (1971).
where C i is the score for column i , and C is the number of categories or columns. You can specify the score type using the SCORES= option in the TABLES statement; if you do not specify the SCORES= option, PROC FREQ uses table scores. For numeric variables, table scores are the values of the numeric row and column headings. You can assign numeric values to the categories in a way that reflects their level of similarity. For example, suppose you have four categories and order them according to similarity. If you assign them values of 0, 2, 4, and 10, the following weights are used for computing the weighted kappa coefficient: w 12 = 0.8, w 13 = 0.6, w 14 = 0, w 23 = 0.8, w 24 = 0.2, and w 34 = 0.4. Note that when there are only two categories (that is, C = 2), the weighted kappa coefficient is identical to the simple kappa coefficient.
If you specify (WT=FC) with the AGREE option in the TABLES statement, PROC FREQ computes Fleiss-Cohen kappa coefficient weights using a form similar to that given by Fleiss and Cohen (1973).
For the preceding example, the weights used for computing the weighted kappa coefficient are: w 12 = 0.96, w 13 = 0.84, w 14 = 0, w 23 = 0.96, w 24 = 0.36, and w 34 = 0.64.
Overall Kappa Coefficient
When there are multiple strata, PROC FREQ combines the stratum-level estimates of kappa into an overall estimate of the supposed common value of kappa. Assume there are q strata, indexed by h = 1 , 2 , . . . , q , and let var ( ![]() h ) denote the squared standard error of
h ) denote the squared standard error of ![]() h . Then the estimate of the overall kappa, according to Fleiss (1981), is computed as
h . Then the estimate of the overall kappa, according to Fleiss (1981), is computed as
PROC FREQ computes an estimate of the overall weighted kappa in a similar manner.
Tests for Equal Kappa Coefficients
When there are multiple strata, the following chi-square statistic tests whether the stratum-level values of kappa are equal.
Under the null hypothesis of equal kappas over the q strata, Q K has an asymptotic chi-square distribution with q ˆ’ 1 degrees of freedom. PROC FREQ computes a test for equal weighted kappa coefficients in a similar manner.
Cochran s Q Test
Cochran s Q is computed for multi-way tables when each variable has two levels, that is, for 2 —2 —2 tables. Cochran s Q statistic is used to test the homogeneity of the one-dimensional margins. Let m denote the number of variables and N denote the total number of subjects. Then Cochran s Q statistic is computed as
where T j is the number of positive responses for variable j , T is the total number of positive responses over all variables, and S k is the number of positive responses for subject k . Under the null hypothesis, Cochran s Q is an approximate chi-square statistic with m ˆ’ 1 degrees of freedom. Refer to Cochran (1950). When there are only two binary response variables ( m = 2), Cochran s Q simplifies to McNemar s test. When there are more than two response categories, you can test for marginal homogeneity using the repeated measures capabilities of the CATMOD procedure.
Tables with Zero Rows and Columns
The AGREE statistics are defined only for square tables, where the number of rows equals the number of columns. If the table is not square, PROC FREQ does not compute AGREE statistics. In the kappa statistic framework, where two independent raters assign ratings to each of n subjects, suppose one of the raters does not use all possible r rating levels. If the corresponding table has r rows but only r ˆ’ 1 columns, then the table is not square, and PROC FREQ does not compute the AGREE statistics. To create a square table in this situation, use the ZEROS option in the WEIGHT statement, which requests that PROC FREQ include observations with zero weights in the analysis. And input zero-weight observations to represent any rating levels that are not used by a rater, so that the input data set has at least one observation for each possible rater and rating combination. This includes all rating levels in the analysis, whether or not all levels are actually assigned by both raters. The resulting table is a square table, r — r , and so all AGREE statistics can be computed.
For more information, see the description of the ZEROS option. By default, PROC FREQ does not process observations that have zero weights, because these observations do not contribute to the total frequency count, and because any resulting zero-weight row or column causes many of the tests and measures of association to be undefined . However, kappa statistics are defined for tables with a zero-weight row or column, and the ZEROS option allows input of zero-weight observations so you can construct the tables needed to compute kappas.
Cochran-Mantel-Haenszel Statistics
For n -way crosstabulation tables, consider the following example:
proc freq; tables A*B*C*D / cmh; run;
The CMH option in the TABLES statement gives a stratified statistical analysis of the relationship between C and D, after controlling for A and B. The stratified analysis provides a way to adjust for the possible confounding effects of A and B without being forced to estimate parameters for them. The analysis produces Cochran-Mantel-Haenszel statistics, and for 2 —2 tables, it includes estimation of the common odds ratio, common relative risks, and the Breslow-Day test for homogeneity of the odds ratios.
Let the number of strata be denoted by q , indexing the strata by h = 1 , 2 , , q . Each stratum contains a contingency table with X representing the row variable and Y representing the column variable. For table h , denote the cell frequency in row i and column j by n hij , with corresponding row and column marginal totals denoted by n hi. and n h.j , and the overall stratum total by n h .
Because the formulas for the Cochran-Mantel-Haenszel statistics are more easily defined in terms of matrices, the following notation is used. Vectors are presumed to be column vectors unless they are transposed ( ² ).
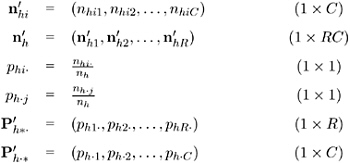
Assume that the strata are independent and that the marginal totals of each stratum are fixed. The null hypothesis, H , is that there is no association between X and Y in any of the strata. The corresponding model is the multiple hypergeometric; this implies that, under H , the expected value and covariance matrix of the frequencies are, respectively,
and
where
and where ![]() denotes Kronecker product multiplication and D a is a diagonal matrix with elements of a on the main diagonal.
denotes Kronecker product multiplication and D a is a diagonal matrix with elements of a on the main diagonal.
The generalized CMH statistic (Landis, Heyman, and Koch 1978) is defined as
where
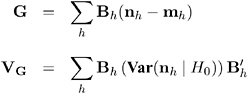
and where
is a matrix of fixed constants based on column scores C h and row scores R h . When the null hypothesis is true, the CMH statistic has an asymptotic chi-square distribution with degrees of freedom equal to the rank of B h . If V G is found to be singular, PROC FREQ prints a message and sets the value of the CMH statistic to missing.
PROC FREQ computes three CMH statistics using this formula for the generalized CMH statistic, with different row and column score definitions for each statistic. The CMH statistics that PROC FREQ computes are the correlation statistic, the ANOVA (row mean scores) statistic, and the general association statistic. These statistics test the null hypothesis of no association against different alternative hypotheses. The following sections describe the computation of these CMH statistics.
CAUTION: The CMH statistics have low power for detecting an association in which the patterns of association for some of the strata are in the opposite direction of the patterns displayed by other strata. Thus, a nonsignificant CMH statistic suggests either that there is no association or that no pattern of association has enough strength or consistency to dominate any other pattern.
Correlation Statistic
The correlation statistic, popularized by Mantel and Haenszel (1959) and Mantel (1963), has one degree of freedom and is known as the Mantel-Haenszel statistic.
The alternative hypothesis for the correlation statistic is that there is a linear association between X and Y in at least one stratum. If either X or Y does not lie on an ordinal (or interval) scale, then this statistic is not meaningful.
To compute the correlation statistic, PROC FREQ uses the formula for the generalized CMH statistic with the row and column scores determined by the SCORES= option in the TABLES statement. See the section Scores on page 102 for more information on the available score types. The matrix of row scores R h has dimension 1 — R , and the matrix of column scores C h has dimension 1 — C .
When there is only one stratum, this CMH statistic reduces to ( n ˆ’ 1) r 2 , where r is the Pearson correlation coefficient between X and Y . When nonparametric (RANK or RIDIT) scores are specified, then the statistic reduces to ![]() , where r s is the Spearman rank correlation coefficient between X and Y . When there is more than one stratum, then this CMH statistic becomes a stratum-adjusted correlation statistic.
, where r s is the Spearman rank correlation coefficient between X and Y . When there is more than one stratum, then this CMH statistic becomes a stratum-adjusted correlation statistic.
ANOVA (Row Mean Scores) Statistic
The ANOVA statistic can be used only when the column variable Y lies on an ordinal (or interval) scale so that the mean score of Y is meaningful. For the ANOVA statistic, the mean score is computed for each row of the table, and the alternative hypothesis is that, for at least one stratum, the mean scores of the R rows are unequal . In other words, the statistic is sensitive to location differences among the R distributions of Y .
The matrix of column scores C h has dimension 1 — C , the column scores are determined by the SCORES= option.
The matrix of row scores R h has dimension ( R ˆ’ 1) — R and is created internally by PROC FREQ as
where I R ˆ’ 1 is an identity matrix of rank R ˆ’ 1, and J R ˆ’ 1 is an ( R ˆ’ 1) — 1 vector of ones. This matrix has the effect of forming R ˆ’ 1 independent contrasts of the R mean scores.
When there is only one stratum, this CMH statistic is essentially an analysis of variance (ANOVA) statistic in the sense that it is a function of the variance ratio F statistic that would be obtained from a one-way ANOVA on the dependent variable Y . If nonparametric scores are specified in this case, then the ANOVA statistic is a Kruskal-Wallis test.
If there is more than one stratum, then this CMH statistic corresponds to a stratum-adjusted ANOVA or Kruskal-Wallis test. In the special case where there is one subject per row and one subject per column in the contingency table of each stratum, this CMH statistic is identical to Friedman s chi-square. See Example 2.8 on page 180 for an illustration.
General Association Statistic
The alternative hypothesis for the general association statistic is that, for at least one stratum, there is some kind of association between X and Y . This statistic is always interpretable because it does not require an ordinal scale for either X or Y .
For the general association statistic, the matrix R h is the same as the one used for the ANOVA statistic. The matrix C h is defined similarly as
PROC FREQ generates both score matrices internally. When there is only one stratum, then the general association CMH statistic reduces to Q P ( n ˆ’ 1) /n , where Q P is the Pearson chi-square statistic. When there is more than one stratum, then the CMH statistic becomes a stratum-adjusted Pearson chi-square statistic. Note that a similar adjustment can be made by summing the Pearson chi-squares across the strata. However, the latter statistic requires a large sample size in each stratum to support the resulting chi-square distribution with q ( R ˆ’ 1)( C ˆ’ 1) degrees of freedom. The CMH statistic requires only a large overall sample size since it has only ( R ˆ’ 1)( C ˆ’ 1) degrees of freedom.
Refer to Cochran (1954); Mantel and Haenszel (1959); Mantel (1963); Birch (1965); Landis, Heyman, and Koch (1978).
Adjusted Odds Ratio and Relative Risk Estimates
The CMH option provides adjusted odds ratio and relative risk estimates for stratified 2 —2 tables. For each of these measures, PROC FREQ computes the Mantel-Haenszel estimate and the logit estimate. These estimates apply to n -way table requests in the TABLES statement, when the row and column variables both have only two levels.
For example,
proc freq; tables A*B*C*D / cmh; run;
In this example, if the row and columns variables C and D both have two levels, PROC FREQ provides odds ratio and relative risk estimates, adjusting for the confounding variables A and B .
The choice of an appropriate measure depends on the study design. For case-control (retrospective) studies, the odds ratio is appropriate. For cohort (prospective) or cross-sectional studies, the relative risk is appropriate. See the section Odds Ratio and Relative Risks for 2 — 2 Tables beginning on page 122 for more information on these measures.
Throughout this section, z denotes the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution.
Odds Ratio, Case-Control Studies
Mantel-Haenszel Estimator
The Mantel-Haenszel estimate of the common odds ratio is computed as
It is always computed unless the denominator is zero. Refer to Mantel and Haenszel (1959) and Agresti (1990).
Using the estimated variance for log(OR MH ) given by Robins, Breslow, and Greenland (1986), PROC FREQ computes the corresponding 100(1 ˆ’ ± )% confidence limits for the odds ratio as
where
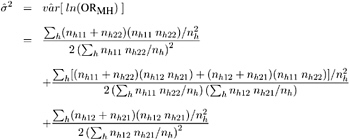
Note that the Mantel-Haenszel odds ratio estimator is less sensitive to small n h than the logit estimator.
Logit Estimator
The adjusted logit estimate of the odds ratio (Woolf 1955) is computed as
and the corresponding 100(1 ˆ’ ± )% confidence limits are
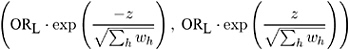
where OR h is the odds ratio for stratum h , and
If any cell frequency in a stratum h is zero, then PROC FREQ adds 0 . 5 to each cell of the stratum before computing OR h and w h (Haldane 1955), and prints a warning.
Exact Confidence Limits for the Common Odds Ratio
When you specify the COMOR option in the EXACT statement, PROC FREQ computes exact confidence limits for the common odds ratio for stratified 2 —2 tables.
This computation assumes that the odds ratio is constant over all the 2 — 2 tables. Exact confidence limits are constructed from the distribution of S = h n h 11 , conditional on the marginal totals of the 2 — 2 tables.
Because this is a discrete problem, the confidence coefficient for these exact confidence limits is not exactly 1 ˆ’ ± but is at least 1 ˆ’ ± . Thus, these confidence limits are conservative. Refer to Agresti (1992).
PROC FREQ computes exact confidence limits for the common odds ratio with an algorithm based on that presented by Vollset, Hirji, and Elashoff (1991). Refer also to Mehta, Patel, and Gray (1985).
Conditional on the marginal totals of 2 — 2 table h , let the random variable S h denote the frequency of table cell (1 , 1). Given the row totals n h 1 . and n h 2 . and column totals n h .1 and n h .2 , the lower and upper bounds for S h are l h and u h ,
Let C s h denote the hypergeometric coefficient,
and let ![]() denote the common odds ratio. Then the conditional distribution of S h is
denote the common odds ratio. Then the conditional distribution of S h is
Summing over all the 2 — 2 tables, S = h S h , and the lower and upper bounds of S are l and u ,
The conditional distribution of the sum S is
where
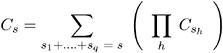
Let s denote the observed sum of cell (1,1) frequencies over the q tables. The following two equations are solved iteratively for lower and upper confidence limits for the common odds ratio, ![]() 1 and
1 and ![]() 2 ,
2 ,
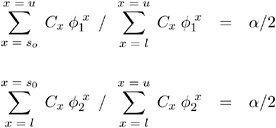
When the observed sum s equals the lower bound l , then PROC FREQ sets the lower exact confidence limit to zero and determines the upper limit with level ± . Similarly, when the observed sum s equals the upper bound u , then PROC FREQ sets the upper exact confidence limit to infinity and determines the lower limit with level ± .
When you specify the COMOR option in the EXACT statement, PROC FREQ also computes the exact test that the common odds ratio equals one. Setting ![]() = 1, the conditional distribution of the sum S under the null hypothesis becomes
= 1, the conditional distribution of the sum S under the null hypothesis becomes
The point probability for this exact test is the probability of the observed sum s under the null hypothesis, conditional on the marginals of the stratified 2 —2 tables, and is denoted by P ( s ). The expected value of S under the null hypothesis is
The one-sided exact p -value is computed from the conditional distribution as P ( S > = s ) or P ( S ‰ s ), depending on whether the observed sum s is greater or less than E ( S ).
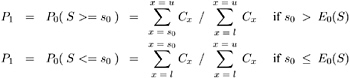
PROC FREQ computes two-sided p -values for this test according to three different definitions. A two-sided p -value is computed as twice the one-sided p -value, setting the result equal to one if it exceeds one.
Additionally, a two-sided p -value is computed as the sum of all probabilities less than or equal to the point probability of the observed sum s , summing over all possible values of s , l ‰ s ‰ u .
Also, a two-sided p -value is computed as the sum of the one-sided p -value and the corresponding area in the opposite tail of the distribution, equidistant from the expected value.
Relative Risks, Cohort Studies
Mantel-Haenszel Estimator
The Mantel-Haenszel estimate of the common relative risk for column 1 is computed as
It is always computed unless the denominator is zero. Refer to Mantel and Haenszel (1959) and Agresti (1990).
Using the estimated variance for log(RR MH ) given by Greenland and Robins (1985), PROC FREQ computes the corresponding 100(1 ˆ’ ± )% confidence limits for the relative risk as
where
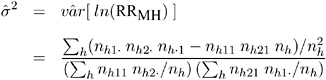
Logit Estimator
The adjusted logit estimate of the common relative risk for column 1 is computed as
and the corresponding 100(1 ˆ’ ± )% confidence limits are

where RR h is the column 1 relative risk estimate for stratum h , and
If n h 11 or n h 21 is zero, then PROC FREQ adds 0 . 5 to each cell of the stratum before computing RR h and w h , and prints a warning. Refer to Kleinbaum, Kupper, and Morgenstern (1982, Sections 17.4 and 17.5).
Breslow-Day Test for Homogeneity of the Odds Ratios
When you specify the CMH option, PROC FREQ computes the Breslow-Day test for stratified analysis of 2 — 2 tables. It tests the null hypothesis that the odds ratios for the q strata are all equal. When the null hypothesis is true, the statistic has approximately a chi-square distribution with q ˆ’ 1 degrees of freedom. Refer to Breslow and Day (1980) and Agresti (1996).
The Breslow-Day statistic is computed as
where E and var denote expected value and variance, respectively. The summation does not include any table with a zero row or column. If OR MH equals zero or if it is undefined , then PROC FREQ does not compute the statistic and prints a warning message.
For the Breslow-Day test to be valid, the sample size should be relatively large in each stratum, and at least 80% of the expected cell counts should be greater than 5. Note that this is a stricter sample size requirement than the requirement for the Cochran-Mantel-Haenszel test for q — 2 — 2 tables, in that each stratum sample size (not just the overall sample size) must be relatively large. Even when the Breslow-Day test is valid, it may not be very powerful against certain alternatives, as discussed in Breslow and Day (1980).
If you specify the BDT option, PROC FREQ computes the Breslow-Day test with Tarone s adjustment, which subtracts an adjustment factor from Q BD to make the resulting statistic asymptotically chi-square.
Refer to Tarone (1985), Jones et al. (1989), and Breslow (1996).
Exact Statistics
Exact statistics can be useful in situations where the asymptotic assumptions are not met, and so the asymptotic p -values are not close approximations for the true p -values. Standard asymptotic methods involve the assumption that the test statistic follows a particular distribution when the sample size is sufficiently large. When the sample size is not large, asymptotic results may not be valid, with the asymptotic p -values differing perhaps substantially from the exact p -values. Asymptotic results may also be unreliable when the distribution of the data is sparse, skewed, or heavily tied. Refer to Agresti (1996) and Bishop, Fienberg, and Holland (1975). Exact computations are based on the statistical theory of exact conditional inference for contingency tables, reviewed by Agresti (1992).
In addition to computation of exact p -values, PROC FREQ provides the option of estimating exact p -values by Monte Carlo simulation. This can be useful for problems that are so large that exact computations require a great amount of time and memory, but for which asymptotic approximations may not be sufficient.
PROC FREQ provides exact p -values for the following tests for two-way tables: Pearson chi-square, likelihood-ratio chi-square, Mantel-Haenszel chi-square, Fisher s exact test, Jonckheere-Terpstra test, Cochran-Armitage test for trend, and McNemar s test. PROC FREQ also computes exact p -values for tests of hypotheses that the following statistics equal zero: Pearson correlation coefficient, Spearman correlation coefficient, simple kappa coefficient, and weighted kappa coefficient. Additionally, PROC FREQ computes exact confidence limits for the odds ratio for 2 — 2 tables. For stratified 2 — 2 tables, PROC FREQ computes exact confidence limits for the common odds ratio, as well as an exact test that the common odds ratio equals one. For one-way frequency tables, PROC FREQ provides the exact chi-square goodness-of-fit test (for equal proportions or for proportions or frequencies that you specify). Also for one-way tables, PROC FREQ provides exact confidence limits for the binomial proportion and an exact test for the binomial proportion value.
The following sections summarize the exact computational algorithms, define the exact p -values that PROC FREQ computes, discuss the computational resource requirements, and describe the Monte Carlo estimation option.
Computational Algorithms
PROC FREQ computes exact p -values for general R — C tables using the network algorithm developed by Mehta and Patel (1983). This algorithm provides a substantial advantage over direct enumeration, which can be very time-consuming and feasible only for small problems. Refer to Agresti (1992) for a review of algorithms for computation of exact p -values, and refer to Mehta, Patel, and Tsiatis (1984) and Mehta, Patel, and Senchaudhuri (1991) for information on the performance of the network algorithm.
The reference set for a given contingency table is the set of all contingency tables with the observed marginal row and column sums. Corresponding to this reference set, the network algorithm forms a directed acyclic network consisting of nodes in a number of stages. A path through the network corresponds to a distinct table in the reference set. The distances between nodes are defined so that the total distance of a path through the network is the corresponding value of the test statistic. At each node, the algorithm computes the shortest and longest path distances for all the paths that pass through that node. For statistics that can be expressed as a linear combination of cell frequencies multiplied by increasing row and column scores, PROC FREQ computes shortest and longest path distances using the algorithm given in Agresti, Mehta, and Patel (1990). For statistics of other forms, PROC FREQ computes an upper bound for the longest path and a lower bound for the shortest path , following the approach of Valz and Thompson (1994).
The longest and shortest path distances or bounds for a node are compared to the value of the test statistic to determine whether all paths through the node contribute to the p -value, none of the paths through the node contribute to the p -value, or neither of these situations occur. If all paths through the node contribute, the p -value is incre-mented accordingly , and these paths are eliminated from further analysis. If no paths contribute, these paths are eliminated from the analysis. Otherwise, the algorithm continues, still processing this node and the associated paths. The algorithm finishes when all nodes have been accounted for, incrementing the p -value accordingly, or eliminated.
In applying the network algorithm, PROC FREQ uses full precision to represent all statistics, row and column scores, and other quantities involved in the computations. Although it is possible to use rounding to improve the speed and memory requirements of the algorithm, PROC FREQ does not do this since it can result in reduced accuracy of the p -values.
For one-way tables, PROC FREQ computes the exact chi-square goodness-of-fit test by the method of Radlow and Alf (1975). PROC FREQ generates all possible one-way tables with the observed total sample size and number of categories. For each possible table, PROC FREQ compares its chi-square value with the value for the observed table. If the table s chi-square value is greater than or equal to the observed chi-square, PROC FREQ increments the exact p -value by the probability of that table, which is calculated under the null hypothesis using the multinomial frequency distribution. By default, the null hypothesis states that all categories have equal proportions. If you specify null hypothesis proportions or frequencies using the TESTP= or TESTF= option in the TABLES statement, then PROC FREQ calculates the exact chi-square test based on that null hypothesis.
For binomial proportions in one-way tables, PROC FREQ computes exact confidence limits using the F distribution method given in Collett (1991) and also described by Leemis and Trivedi (1996). PROC FREQ computes the exact test for a binomial proportion ( H : p = p ) by summing binomial probabilities over all alternatives. See the section Binomial Proportion on page 118 for details. By default, PROC FREQ uses p = 0 . 5 as the null hypothesis proportion. Alternatively, you can specify the null hypothesis proportion with the P= option in the TABLES statement.
See the section Odds Ratio and Relative Risks for 2 — 2 Tables on page 122 for details on computation of exact confidence limits for the odds ratio for 2 — 2 tables. See the section Exact Confidence Limits for the Common Odds Ratio on page 138 for details on computation of exact confidence limits for the common odds ratio for stratified 2 — 2 tables.
Definition of p-Values
For several tests in PROC FREQ, the test statistic is nonnegative, and large values of the test statistic indicate a departure from the null hypothesis. Such tests include the Pearson chi-square, the likelihood-ratio chi-square, the Mantel-Haenszel chi-square, Fisher s exact test for tables larger than 2 — 2 tables, McNemar s test, and the one-way chi-square goodness-of-fit test. The exact p -value for these nondirectional tests is the sum of probabilities for those tables having a test statistic greater than or equal to the value of the observed test statistic.
There are other tests where it may be appropriate to test against either a one-sided or a two-sided alternative hypothesis. For example, when you test the null hypothesis that the true parameter value equals 0 ( T = 0), the alternative of interest may be one-sided ( T ‰ 0, or T ‰ 0) or two-sided ( T ‰ 0). Such tests include the Pearson correlation coefficient, Spearman correlation coefficient, Jonckheere-Terpstra test, Cochran-Armitage test for trend, simple kappa coefficient, and weighted kappa coefficient. For these tests, PROC FREQ outputs the right-sided p -value when the observed value of the test statistic is greater than its expected value. The right-sided p -value is the sum of probabilities for those tables having a test statistic greater than or equal to the observed test statistic. Otherwise, when the test statistic is less than or equal to its expected value, PROC FREQ outputs the left-sided p -value. The left-sided p -value is the sum of probabilities for those tables having a test statistic less than or equal to the one observed. The one-sided p -value P 1 can be expressed as

where t is the observed value of the test statistic and E ( T ) is the expected value of the test statistic under the null hypothesis. PROC FREQ computes the two-sided p -value as the sum of the one-sided p -value and the corresponding area in the opposite tail of the distribution of the statistic, equidistant from the expected value. The two-sided p -value P 2 can be expressed as
If you specify the POINT option in the EXACT statement, PROC FREQ also displays exact point probabilities for the test statistics. The exact point probability is the exact probability that the test statistic equals the observed value.
Computational Resources
PROC FREQ uses relatively fast and efficient algorithms for exact computations. These recently developed algorithms, together with improvements in computer power, make it feasible now to perform exact computations for data sets where previously only asymptotic methods could be applied. Nevertheless, there are still large problems that may require a prohibitive amount of time and memory for exact computations, depending on the speed and memory available on your computer. For large problems, consider whether exact methods are really needed or whether asymptotic methods might give results quite close to the exact results, while requiring much less computer time and memory. When asymptotic methods may not be sufficient for such large problems, consider using Monte Carlo estimation of exact p -values, as described in the section Monte Carlo Estimation on page 146.
A formula does not exist that can predict in advance how much time and memory are needed to compute an exact p -value for a certain problem. The time and memory required depend on several factors, including which test is being performed, the total sample size, the number of rows and columns, and the specific arrangement of the observations into table cells. Generally, larger problems (in terms of total sample size, number of rows, and number of columns) tend to require more time and memory. Additionally, for a fixed total sample size, time and memory requirements tend to increase as the number of rows and columns increases, since this corresponds to an increase in the number of tables in the reference set. Also for a fixed sample size, time and memory requirements increase as the marginal row and column totals become more homogeneous. Refer to Agresti, Mehta, and Patel (1990) and Gail and Mantel (1977).
At any time while PROC FREQ is computing exact p -values, you can terminate the computations by pressing the system interrupt key sequence (refer to the SAS Companion for your system) and choosing to stop computations. After you terminate exact computations, PROC FREQ completes all other remaining tasks . The procedure produces the requested output and reports missing values for any exact p -values that were not computed by the time of termination.
You can also use the MAXTIME= option in the EXACT statement to limit the amount of time PROC FREQ uses for exact computations. You specify a MAXTIME= value that is the maximum amount of clock time (in seconds) that PROC FREQ can use to compute an exact p -value. If PROC FREQ does not finish computing an exact p -value within that time, it terminates the computation and completes all other remaining tasks.
Monte Carlo Estimation
If you specify the option MC in the EXACT statement, PROC FREQ computes Monte Carlo estimates of the exact p -values instead of directly computing the exact p -values. Monte Carlo estimation can be useful for large problems that require a great amount of time and memory for exact computations but for which asymptotic approximations may not be sufficient. To describe the precision of each Monte Carlo estimate, PROC FREQ provides the asymptotic standard error and 100(1 ˆ’ ± )% confidence limits. The confidence level is determined by the ALPHA= option in the EXACT statement, which, by default, equals 0.01, and produces 99% confidence limits. The N= n option in the EXACT statement specifies the number of samples that PROC FREQ uses for Monte Carlo estimation; the default is 10000 samples. You can specify a larger value for n to improve the precision of the Monte Carlo estimates. Because larger values of n generate more samples, the computation time increases. Alternatively, you can specify a smaller value of n to reduce the computation time.
To compute a Monte Carlo estimate of an exact p -value, PROC FREQ generates a random sample of tables with the same total sample size, row totals, and column totals as the observed table. PROC FREQ uses the algorithm of Agresti, Wackerly, and Boyett (1979), which generates tables in proportion to their hypergeometric probabilities conditional on the marginal frequencies. For each sample table, PROC FREQ computes the value of the test statistic and compares it to the value for the observed table. When estimating a right-sided p -value, PROC FREQ counts all sample tables for which the test statistic is greater than or equal to the observed test statistic. Then the p -value estimate equals the number of these tables divided by the total number of tables sampled.

PROC FREQ computes left-sided and two-sided p -value estimates in a similar manner. For left-sided p -values, PROC FREQ evaluates whether the test statistic for each sampled table is less than or equal to the observed test statistic. For two-sided p -values, PROC FREQ examines the sample test statistics according to the expression for P 2 given in the section Asymptotic Tests on page 109. The variable M is a binomially distributed variable with N trials and success probability p . It follows that the asymptotic standard error of the Monte Carlo estimate is
PROC FREQ constructs asymptotic confidence limits for the p -values according to
where z ± / 2 is the 100(1 ˆ’ ± / 2) percentile of the standard normal distribution, and the confidence level ± is determined by the ALPHA= option in the EXACT statement.
When the Monte Carlo estimate ![]() MC equals 0, then PROC FREQ computes the confidence limits for the p -value as
MC equals 0, then PROC FREQ computes the confidence limits for the p -value as
When the Monte Carlo estimate ![]() MC equals 1, then PROC FREQ computes the confidence limits as
MC equals 1, then PROC FREQ computes the confidence limits as
Computational Resources
For each variable in a table request, PROC FREQ stores all of the levels in memory. If all variables are numeric and not formatted, this requires about 84 bytes for each variable level. When there are character variables or formatted numeric variables, the memory that is required depends on the formatted variable lengths, with longer formatted lengths requiring more memory. The number of levels for each variable is limited only by the largest integer that your operating environment can store.
For any single crosstabulation table requested, PROC FREQ builds the entire table in memory, regardless of whether the table has zero cell counts. Thus, if the numeric variables A , B , and C each have 10 levels, PROC FREQ requires 2520 bytes to store the variable levels for the table request A * B * C , as follows:
3 variables * 10 levels/variable * 84 bytes/level
In addition, PROC FREQ requires 8000 bytes to store the table cell frequencies
1000 cells * 8 bytes/cell
even though there may be only 10 observations.
When the variables have many levels or when there are many multiway tables, your computer may not have enough memory to construct the tables. If PROC FREQ runs out of memory while constructing tables, it stops collecting levels for the variable with the most levels and returns the memory that is used by that variable. The procedure then builds the tables that do not contain the disabled variables.
If there is not enough memory for your table request and if increasing the available memory is impractical , you can reduce the number of multiway tables or variable levels. If you are not using the CMH or AGREE option in the TABLES statement to compute statistics across strata, reduce the number of multiway tables by using PROC SORT to sort the data set by one or more of the variables or by using the DATA step to create an index for the variables. Then remove the sorted or indexed variables from the TABLES statement and include a BY statement that uses these variables. You can also reduce memory requirements by using a FORMAT statement in the PROC FREQ step to reduce the number of levels. Additionally, reducing the formatted variable lengths reduces the amount of memory that is needed to store the variable levels. For more information on using formats, see the Grouping with Formats section on page 99.
Output Data Sets
PROC FREQ produces two types of output data sets that you can use with other statistical and reporting procedures. These data sets are produced as follows:
-
Specifying a TABLES statement with an OUT= option creates an output data set that contains frequency or crosstabulation table counts and percentages.
-
Specifying an OUTPUT statement creates an output data set that contains statistics.
PROC FREQ does not display the output data sets. Use PROC PRINT, PROC REPORT, or any other SAS reporting tool to display an output data set.
Contents of the TABLES Statement Output Data Set
The OUT= option in the TABLES statement creates an output data set that contains one observation for each combination of the variable values (or table cell) in the last table request. By default, each observation contains the frequency and percentage for the table cell. When the input data set contains missing values, the output data set also contains an observation with the frequency of missing values. The output data set includes the following variables:
-
BY variables
-
table request variables, such as A , B , C, and D in the table request A * B * C * D
-
COUNT , a variable containing the cell frequency
-
PERCENT , a variable containing the cell percentage
If you specify the OUTEXPECT and OUTPCT options in the TABLES statement, the output data set also contains expected frequencies and row, column, and table percentages, respectively. The additional variables are
-
EXPECTED , a variable containing the expected frequency
-
PCT “TABL , a variable containing the percentage of two-way table frequency, for n -way tables where n > 2
-
PCT “ROW , a variable containing the percentage of row frequency
-
PCT “COL , a variable containing the percentage of column frequency
If you specify the OUTCUM option in the TABLES statement, the output data set also contains cumulative frequencies and cumulative percentages for one-way tables. The additional variables are
-
CUM “FREQ , a variable containing the cumulative frequency
-
CUM “PCT , a variable containing the cumulative percentage
The OUTCUM option has no effect for two-way or multiway tables.
When you submit the following statements
proc freq; tables A A*B / out=D; run;
the output data set D contains frequencies and percentages for the last table request, A * B . If A has two levels (1 and 2), B has three levels (1,2, and 3), and no table cell count is zero or missing, the output data set D includes six observations, one for each combination of A and B . The first observation corresponds to A =1 and B =1; the second observation corresponds to A =1 and B =2; and so on. The data set includes the variables COUNT and PERCENT . The value of COUNT is the number of observations with the given combination of A and B values. The value of PERCENT is the percent of the total number of observations having that A and B combination.
When PROC FREQ combines different variable values into the same formatted level, the output data set contains the smallest internal value for the formatted level. For example, suppose a variable X has the values 1.1., 1.4, 1.7, 2.1, and 2.3. When you submit the statement
format X 1.;
in a PROC FREQ step, the formatted levels listed in the frequency table for X are 1 and 2. If you create an output data set with the frequency counts, the internal values of X are 1.1 and 1.7. To report the internal values of X when you display the output data set, use a format of 3.1 with X .
Contents of the OUTPUT Statement Output Data Set
The OUTPUT statement creates a SAS data set containing the statistics that PROC FREQ computes for the last table request. You specify which statistics to store in the output data set. There is an observation with the specified statistics for each stratum or two-way table. If PROC FREQ computes summary statistics for a stratified table, the output data set also contains a summary observation with those statistics.
The OUTPUT data set can include the following variables.
-
BY variables
-
variables that identify the stratum, such as A and B in the table request A * B * C * D
-
variables that contain the specified statistics
The output data set also includes variables with the p -values and degrees of freedom, asymptotic standard error (ASE), or confidence limits when PROC FREQ computes these values for a specified statistic.
The variable names for the specified statistics in the output data set are the names of the options enclosed in underscores. PROC FREQ forms variable names for the corresponding p -values, degrees of freedom, or confidence limits by combining the name of the option with the appropriate prefix from the following list:
| DF_ | degrees of freedom |
| E_ | asymptotic standard error (ASE) |
| L_ | lower confidence limit |
| U_ | upper confidence limit |
| E0_ | ASE under the null hypothesis |
| Z_ | standardized value |
| P_ | p -value |
| P2_ | two-sided p -value |
| PL_ | left-sided p -value |
| PR_ | right-sided p -value |
| XP_ | exact p -value |
| XP2_ | exact two-sided p -value |
| XPL_ | exact left-sided p -value |
| XPR_ | exact right-sided p -value |
| XPT_ | exact point probability |
| XL_ | exact lower confidence limit |
| XR_ | exact upper confidence limit |
For example, variable names created for the Pearson chi-square, its degrees of freedom, its p -values are _PCHI_ , DF_PCHI , and P_PCHI , respectively.
If the length of the prefix plus the statistic option exceeds eight characters, PROC FREQ truncates the option so that the name of the new variable is eight characters long.
Displayed Output
Number of Variable Levels Table
If you specify the NLEVELS option in the PROC FREQ statement, PROC FREQ displays the Number of Variable Levels table. This table provides the number of levels for all variables named in the TABLES statements. PROC FREQ determines the variable levels from the formatted variable values. See Grouping with Formats for details. The Number of Variable Levels table contains the following information:
-
Variable name
-
Levels, which is the total number of levels of the variable
-
Number of Nonmissing Levels, if there are missing levels for any of the variables
-
Number of Missing Levels, if there are missing levels for any of the variables
One-Way Frequency Tables
PROC FREQ displays one-way frequency tables for all one-way table requests in the TABLES statements, unless you specify the NOPRINT option in the PROC statement or the NOPRINT option in the TABLES statement. For a one-way table showing the frequency distribution of a single variable, PROC FREQ displays the following information:
-
the name of the variable and its values
-
Frequency counts, giving the number of observations that have each value
-
specified Test Frequency counts, if you specify the CHISQ and TESTF= options to request a chi-square goodness-of-fit test for specified frequencies
-
Percent, giving the percentage of the total number of observations with that value. (The NOPERCENT option suppresses this information.)
-
specified Test Percents, if you specify the CHISQ and TESTP= options to request a chi-square goodness-of-fit test for specified percents. (The NOPERCENT option suppresses this information.)
-
Cumulative Frequency counts, giving the sum of the frequency counts of that value and all other values listed above it in the table. The last cumulative frequency is the total number of nonmissing observations. (The NOCUM option suppresses this information.)
-
Cumulative Percent values, giving the percentage of the total number of observations with that value and all others previously listed in the table. (The NOCUM or the NOPERCENT option suppresses this information.)
The one-way table also displays the Frequency Missing, or the number of observations with missing values.
Statistics for One-Way Frequency Tables
For one-way tables, two statistical options are available in the TABLES statement. The CHISQ option provides a chi-square goodness-of-fit test, and the BINOMIAL option provides binomial proportion statistics. PROC FREQ displays the following information, unless you specify the NOPRINT option in the PROC statement:
-
If you specify the CHISQ option for a one-way table, PROC FREQ provides a chi-square goodness-of-fit test, displaying the Chi-Square statistic, the degrees of freedom (DF), and the probability value (Pr > ChiSq). If you specify the CHISQ option in the EXACT statement, PROC FREQ also displays the exact probability value for this test. If you specify the POINT option with the CHISQ option in the EXACT statement, PROC FREQ displays the exact point probability for the test statistic.
-
If you specify the BINOMIAL option for a one-way table, PROC FREQ displays the estimate of the binomial Proportion, which is the proportion of observations in the first class listed in the one-way table. PROC FREQ also displays the asymptotic standard error (ASE) and the asymptotic and exact confidence limits for this estimate. For the binomial proportion test, PROC FREQ displays the asymptotic standard error under the null hypothesis (ASE Under H0), the standardized test statistic (Z), and the one-sided and two-sided probability values. If you specify the BINOMIAL option in the EXACT statement, PROC FREQ also displays the exact one-sided and two-sided probability values for this test. If you specify the POINT option with the BINOMIAL option in the EXACT statement, PROC FREQ displays the exact point probability for the test.
Multiway Tables
PROC FREQ displays all multiway table requests in the TABLES statements, unless you specify the NOPRINT option in the PROC statement or the NOPRINT option in the TABLES statement.
For two-way to multiway crosstabulation tables, the values of the last variable in the table request form the table columns. The values of the next -to-last variable form the rows. Each level (or combination of levels) of the other variables forms one stratum.
There are three ways to display multiway tables in PROC FREQ. By default, PROC FREQ displays multiway tables as separate two-way crosstabulation tables for each stratum of the multiway table. Also by default, PROC FREQ displays these two-way crosstabulation tables in table cell format. Alternatively, if you specify the CROSSLIST option, PROC FREQ displays the two-way crosstabulation tables in ODS column format. If you specify the LIST option, PROC FREQ displays multiway tables in list format.
Crosstabulation Tables
By default, PROC FREQ displays two-way crosstabulation tables in table cell format. The row variable values are listed down the side of the table, the column variable values are listed across the top of the table, and each row and column variable level combination forms a table cell.
Each cell of a crosstabulation table may contain the following information:
-
Frequency, giving the number of observations that have the indicated values of the two variables. (The NOFREQ option suppresses this information.)
-
the Expected cell frequency under the hypothesis of independence, if you specify the EXPECTED option
-
the Deviation of the cell frequency from the expected value, if you specify the DEVIATION option
-
Cell Chi-Square, which is the cell s contribution to the total chi-square statistic, if you specify the CELLCHI2 option
-
Tot Pct, or the cell s percentage of the total frequency, for n -way tables when n > 2, if you specify the TOTPCT option
-
Percent, the cell s percentage of the total frequency. (The NOPERCENT option suppresses this information.)
-
Row Pct, or the row percentage, the cell s percentage of the total frequency count for that cell s row. (The NOROW option suppresses this information.)
-
Col Pct, or column percentage, the cell s percentage of the total frequency count for that cell s column. (The NOCOL option suppresses this information.)
-
Cumulative Col%, or cumulative column percent, if you specify the CUMCOL option
The table also displays the Frequency Missing, or the number of observations with missing values.
CROSSLIST Tables
If you specify the CROSSLIST option, PROC FREQ displays two-way crosstabulation tables with ODS column format. Using column format, a CROSSLIST table provides the same information (frequencies, percentages, and other statistics) as the default crosstabulation table with cell format. But unlike the default crosstabulation table, a CROSSLIST table has a table definition that you can customize with PROC TEMPLATE. For more information, refer to the chapter titled The TEMPLATE Procedure in the SAS Output Delivery System User s Guide .
In the CROSSLIST table format, the rows of the display correspond to the crosstabulation table cells, and the columns of the display correspond to descriptive statistics such as frequencies and percentages. Each table cell is identified by the values of its TABLES row and column variable levels, with all column variable levels listed within each row variable level. The CROSSLIST table also provides row totals, column totals, and overall table totals.
For a crosstabulation table in the CROSSLIST format, PROC FREQ displays the following information:
-
the row variable name and values
-
the column variable name and values
-
Frequency, giving the number of observations that have the indicated values of the two variables. (The NOFREQ option suppresses this information.)
-
the Expected cell frequency under the hypothesis of independence, if you specify the EXPECTED option
-
the Deviation of the cell frequency from the expected value, if you specify the DEVIATION option
-
Cell Chi-Square, which is the cell s contribution to the total chi-square statistic, if you specify the CELLCHI2 option
-
Total Percent, or the cell s percentage of the total frequency, for n -way tables when n > 2, if you specify the TOTPCT option
-
Percent, the cell s percentage of the total frequency. (The NOPERCENT option suppresses this information.)
-
Row Percent, the cell s percentage of the total frequency count for that cell s row. (The NOROW option suppresses this information.)
-
Column Percent, the cell s percentage of the total frequency count for that cell s column. (The NOCOL option suppresses this information.)
The table also displays the Frequency Missing, or the number of observations with missing values.
LIST Tables
If you specify the LIST option in the TABLES statement, PROC FREQ displays multiway tables in a list format rather than as crosstabulation tables. The LIST option displays the entire multiway table in one table, instead of displaying a separate two-way table for each stratum. The LIST option is not available when you also request statistical options. Unlike the default crosstabulation output, the LIST output does not display row percentages, column percentages, and optional information such as expected frequencies and cell chi-squares.
For a multiway table in list format, PROC FREQ displays the following information:
-
the variable names and values
-
Frequency counts, giving the number of observations with the indicated combination of variable values
-
Percent, the cell s percentage of the total number of observations. (The NOPERCENT option suppresses this information.)
-
Cumulative Frequency counts, giving the sum of the frequency counts of that cell and all other cells listed above it in the table. The last cumulative frequency is the total number of nonmissing observations. (The NOCUM option suppresses this information.)
-
Cumulative Percent values, giving the percentage of the total number of observations for that cell and all others previously listed in the table. (The NOCUM or the NOPERCENT option suppresses this information.)
The table also displays the Frequency Missing, or the number of observations with missing values.
Statistics for Multiway Tables
PROC FREQ computes statistical tests and measures for crosstabulation tables, depending on which statements and options you specify. You can suppress the display of all these results by specifying the NOPRINT option in the PROC statement. With any of the following information, PROC FREQ also displays the Sample Size and the Frequency Missing.
-
If you specify the SCOROUT option, PROC FREQ displays the Row Scores and Column Scores that it uses for statistical computations. The Row Scores table displays the row variable values and the Score corresponding to each value. The Column Scores table displays the column variable values and the corresponding Scores. PROC FREQ also identifies the score type used to compute the row and column scores. You can specify the score type with the SCORES= option in the TABLES statement.
-
If you specify the CHISQ option, PROC FREQ displays the following statistics for each two-way table: Pearson Chi-Square, Likelihood-Ratio Chi-Square, Continuity-Adjusted Chi-Square (for 2 —2 tables), Mantel-Haenszel Chi-Square, the Phi Coefficient, the Contingency Coefficient, and Cramer s V . For each test statistic, PROC FREQ also displays the degrees of freedom (DF) and the probability value (Prob).
-
If you specify the CHISQ option for 2 —2 tables, PROC FREQ also displays Fisher s exact test. The test output includes the cell (1,1) frequency (F), the exact left-sided and right-sided probability values, the table probability (P), and the exact two-sided probability value.
-
If you specify the FISHER option in the TABLES statement (or, equivalently, the FISHER option in the EXACT statement), PROC FREQ displays Fisher s exact test for tables larger than 2 —2. The test output includes the table probability (P) and the probability value. In addition, PROC FREQ displays the CHISQ output listed earlier, even if you do not also specify the CHISQ option.
-
If you specify the PCHI, LRCHI, or MHCHI option in the EXACT statement, PROC FREQ also displays the corresponding exact test: Pearson Chi-Square, Likelihood-Ratio Chi-Square, or Mantel-Haenszel Chi-Square, respectively. The test output includes the test statistic, the degrees of freedom (DF), and the asymptotic and exact probability values. If you also specify the POINT option in the EXACT statement, PROC FREQ displays the point probability for each exact test requested. If you specify the CHISQ option in the EXACT statement, PROC FREQ displays exact probability values for all three of these chi-square tests.
-
If you specify the MEASURES option, PROC FREQ displays the following statistics and their asymptotic standard errors (ASE) for each two-way table: Gamma, Kendall s Tau- b , Stuart s Tau- c , Somers D ( C R ), Somers D ( R C ), Pearson Correlation, Spearman Correlation, Lambda Asymmetric ( C R ), Lambda Asymmetric ( R C ), Lambda Symmetric, Uncertainty Coefficient ( C R ), Uncertainty Coefficient ( R C ), and Uncertainty Coefficient Symmetric. If you specify the CL option, PROC FREQ also displays confidence limits for these measures.
-
If you specify the PLCORR option, PROC FREQ displays the tetrachoric correlation for 2 —2 tables or the polychoric correlation for larger tables. In addition, PROC FREQ displays the MEASURES output listed earlier, even if you do not also specify the MEASURES option.
-
If you specify the option GAMMA, KENTB, STUTC, SMDCR, SMDRC, PCORR, or SCORR in the TEST statement, PROC FREQ displays asymptotic tests for Gamma, Kendall s Tau- b , Stuart s Tau- c , Somers D ( C R ), Somers D ( R C ), the Pearson Correlation, or the Spearman Correlation, respectively. If you specify the MEASURES option in the TEST statement, PROC FREQ displays all these asymptotic tests. The test output includes the statistic, its asymptotic standard error (ASE), Confidence Limits, the ASE under the null hypothesis H0, the standardized test statistic (Z), and the one-sided and two-sided probability values.
-
If you specify the PCORR or SCORR option in the EXACT statement, PROC FREQ displays asymptotic and exact tests for the Pearson Correlation or the Spearman Correlation, respectively. The test output includes the correlation, its asymptotic standard error (ASE), Confidence Limits, the ASE under the null hypothesis H0, the standardized test statistic (Z), and the asymptotic and exact one-sided and two-sided probability values. If you also specify the POINT option in the EXACT statement, PROC FREQ displays the point probability for each exact test requested.
-
If you specify the RISKDIFF option for 2 — 2 tables, PROC FREQ displays the Column 1 and Column 2 Risk Estimates. For each column, PROC FREQ displays Row 1 Risk, Row 2 Risk, Total Risk, and Risk Difference, together with their asymptotic standard errors (ASE), Asymptotic Confidence Limits, and Exact Confidence Limits. Exact confidence limits are not available for the risk difference.
-
If you specify the MEASURES option or the RELRISK option for 2 — 2 tables, PROC FREQ displays Estimates of the Relative Risk for Case-Control and Cohort studies, together with their Confidence Limits. These measures are also known as the Odds Ratio and the Column 1 and 2 Relative Risks. If you specify the OR option in the EXACT statement, PROC FREQ also displays Exact Confidence Limits for the Odds Ratio.
-
If you specify the TREND option, PROC FREQ displays the Cochran-Armitage Trend Test for tables that are 2 — C or R — 2. For this test, PROC FREQ gives the Statistic (Z) and the one-sided and two-sided probability values. If you specify the TREND option in the EXACT statement, PROC FREQ also displays the exact one-sided and two-sided probability values for this test. If you specify the POINT option with the TREND option in the EXACT statement, PROC FREQ displays the exact point probability for the test statistic.
-
If you specify the JT option, PROC FREQ displays the Jonckheere-Terpstra Test, showing the Statistic (JT), the standardized test statistic (Z), and the one-sided and two-sided probability values. If you specify the JT option in the EXACT statement, PROC FREQ also displays the exact one-sided and two-sided probability values for this test. If you specify the POINT option with the JT option in the EXACT statement, PROC FREQ displays the exact point probability for the test statistic.
-
If you specify the AGREE option and the PRINTKWT option, PROC FREQ displays the Kappa Coefficient Weights for square tables greater than 2 —2.
-
If you specify the AGREE option, for two-way tables PROC FREQ displays McNemar s Test and the Simple Kappa Coefficient for 2 —2 tables. For square tables larger than 2 —2, PROC FREQ displays Bowker s Test of Symmetry, the Simple Kappa Coefficient, and the Weighted Kappa Coefficient. For McNemar s Test and Bowker s Test of Symmetry, PROC FREQ displays the Statistic (S), the degrees of freedom (DF), and the probability value (Pr > S). If you specify the MCNEM option in the EXACT statement, PROC FREQ also displays the exact probability value for McNemar s test. If you specify the POINT option with the MCNEM option in the EXACT statement, PROC FREQ displays the exact point probability for the test statistic. For the simple and weighted kappa coefficients, PROC FREQ displays the kappa values, asymptotic standard errors (ASE), and Confidence Limits.
-
If you specify the KAPPA or WTKAP option in the TEST statement, PROC FREQ displays asymptotic tests for the simple kappa coefficient or the weighted kappa coefficient, respectively. If you specify the AGREE option in the TEST statement, PROC FREQ displays both these asymptotic tests. The test output includes the kappa coefficient, its asymptotic standard error (ASE), Confidence Limits, the ASE under the null hypothesis H0, the standardized test statistic (Z), and the one-sided and two-sided probability values.
-
If you specify the KAPPA or WTKAP option in the EXACT statement, PROC FREQ displays asymptotic and exact tests for the simple kappa coefficient or the weighted kappa coefficient, respectively. The test output includes the kappa coefficient, its asymptotic standard error (ASE), Confidence Limits, the ASE under the null hypothesis H0, the standardized test statistic (Z), and the asymptotic and exact one-sided and two-sided probability values. If you specify the POINT option in the EXACT statement, PROC FREQ displays the point probability for each exact test requested.
-
If you specify the MC option in the EXACT statement, PROC FREQ displays Monte Carlo estimates for all exact p -values requested by statistic-options in the EXACT statement. The Monte Carlo output includes the p -value Estimate, its Confidence Limits, the Number of Samples used to compute the Monte Carlo estimate, and the Initial Seed for random number generation.
-
If you specify the AGREE option, for multiple strata PROC FREQ displays Overall Simple and Weighted Kappa Coefficients, with their asymptotic standard errors (ASE) and Confidence Limits. PROC FREQ also displays Tests for Equal Kappa Coefficients, giving the Chi-Squares, degrees of freedom (DF), and probability values (Pr > ChiSq) for the Simple Kappa and Weighted Kappa. For multiple strata of 2 —2 tables, PROC FREQ displays Cochran s Q , giving the Statistic (Q), the degrees of freedom (DF), and the probability value (Pr >Q).
-
If you specify the CMH option, PROC FREQ displays Cochran-Mantel-Haenszel Statistics for the following three alternative hypotheses: Nonzero Correlation, Row Mean Scores Differ (ANOVA Statistic), and General Association. For each of these statistics, PROC FREQ gives the degrees of freedom (DF) and the probability value (Prob). For 2 —2 tables, PROC FREQ also displays Estimates of the Common Relative Risk for Case-Control and Cohort studies, together with their confidence limits. These include both Mantel-Haenszel and Logit stratum-adjusted estimates of the common Odds Ratio, Column 1 Relative Risk, and Column 2 Relative Risk. Also for 2 —2 tables, PROC FREQ displays the Breslow-Day Test for Homogeneity of the Odds Ratios. For this test, PROC FREQ gives the Chi-Square, the degrees of freedom (DF), and the probability value (Pr > ChiSq).
-
If you specify the CMH option in the TABLES statement and also specify the COMOR option in the EXACT statement, PROC FREQ displays exact confidence limits for the Common Odds Ratio for multiple strata of 2 —2 tables. PROC FREQ also displays the Exact Test of H0: Common Odds Ratio = 1. The test output includes the Cell (1,1) Sum (S), Mean of S Under H0, One-sided Pr <= S, and Point Pr = S. PROC FREQ also provides exact two-sided probability values for the test, computed according to the following three methods: 2 * One-sided, Sum of probabilities <= Point probability, and Pr >= S - Mean.
ODS Table Names
PROC FREQ assigns a name to each table it creates. You can use these names to reference the table when using the Output Delivery System (ODS) to select tables and create output data sets. For more information on ODS, see Chapter 14, Using the Output Delivery System. ( SAS/STAT User s Guide )
Table 2.11 lists the ODS table names together with their descriptions and the options required to produce the tables. Note that the ALL option in the TABLES statement invokes the CHISQ, MEASURES, and CMH options.
| ODS Table Name | Description | Statement | Option |
|---|---|---|---|
| BinomialProp | Binomial proportion | TABLES | BINOMIAL (one-way tables) |
| BinomialPropTest | Binomial proportion test | TABLES | BINOMIAL (one-way tables) |
| BreslowDayTest | Breslow-Day test | TABLES | CMH ( h —2 —2 tables) |
| CMH | Cochran-Mantel-Haenszel statistics | TABLES | CMH |
| ChiSq | Chi-square tests | TABLES | CHISQ |
| CochransQ | Cochran s Q | TABLES | AGREE ( h —2 —2 tables) |
| ColScores | Column scores | TABLES | SCOROUT |
| CommonOddsRatioCL | Exact confidence limits for the common odds ratio | EXACT | COMOR |
| CommonOddsRatioTest | Common odds ratio exact test | EXACT | COMOR |
| CommonRelRisks | Common relative risks | TABLES | CMH ( h —2 —2 tables) |
| CrossList | Column format crosstabulation table | TABLES | CROSSLIST ( n -way table request, n > 1) |
| CrossTabFreqs | Crosstabulation table | TABLES | ( n -way table request, n > 1) |
| EqualKappaTest | Test for equal simple kappas | TABLES | AGREE ( h —2 —2 tables) |
| EqualKappaTests | Tests for equal kappas | TABLES | AGREE ( h — r — r tables, r > 2) |
| FishersExact | Fisher s exact test | EXACT or TABLES or TABLES | FISHER or EXACT FISHER CHISQ (2 —2 tables) |
| FishersExactMC | Monte Carlo estimates for Fisher s exact test | EXACT | FISHER / MC |
| Gamma | Gamma | TEST | GAMMA |
| GammaTest | Gamma test | TEST | GAMMA |
| JTTest | Jonckheere-Terpstra test | TABLES | JT |
| JTTestMC | Monte Carlo estimates for the JT exact test | EXACT | JT / MC |
| KappaStatistics | Kappa statistics | TABLES | AGREE ( r — r tables, r > 2, and no TEST or EXACT KAPPA) |
| KappaWeights | Kappa weights | TABLES | AGREE and PRINTKWT |
| List | List format multiway table | TABLES | LIST |
| LRChiSq | Likelihood-ratio chi-square exact test | EXACT | LRCHI |
| LRChiSqMC | Monte Carlo exact test for likelihood-ratio chi-square | EXACT | LRCHI / MC |
| McNemarsTest | McNemar s test | TABLES | AGREE (2 —2 tables) |
| Measures | Measures of association | TABLES | MEASURES |
| MHChiSq | Mantel-Haenszel chi-square exact test | EXACT | MHCHI |
| MHChiSqMC | Monte Carlo exact test for Mantel-Haenszel chi-square | EXACT | MHCHI / MC |
| NLevels | Number of variable levels | PROC | NLEVELS |
| OddsRatioCL | Exact confidence limits for the odds ratio | EXACT | OR |
| OneWayChiSq | One-way chi-square test | TABLES | CHISQ (one-way tables) |
| OneWayChiSqMC | Monte Carlo exact test for one-way chi-square | EXACT | CHISQ / MC (one-way tables) |
| OneWayFreqs | One-way frequencies | PROC or TABLES | (with no TABLES stmt) (one-way table request) |
| OverallKappa | Overall simple kappa | TABLES | AGREE ( h —2 —2 tables) |
| OverallKappas | Overall kappa coefficients | TABLES | AGREE ( h — r — r tables, r > 2) |
| PearsonChiSq | Pearson chi-square exact test | EXACT | PCHI |
| PearsonChiSqMC | Monte Carlo exact test for Pearson chi-square | EXACT | PCHI / MC |
| PearsonCorr | Pearson correlation | TEST or EXACT | PCORR PCORR |
| PearsonCorrMC | Monte Carlo exact test for Pearson correlation | EXACT | PCORR / MC |
| PearsonCorrTest | Pearson correlation test | TEST or EXACT | PCORR PCORR |
| RelativeRisks | Relative risk estimates | TABLES | RELRISK or MEASURES (2 — 2 tables) |
| RiskDiffCol1 | Column 1 risk estimates | TABLES | RISKDIFF (2 — 2 tables) |
| RiskDiffCol2 | Column 2 risk estimates | TABLES | RISKDIFF (2 — 2 tables) |
| RowScores | Row scores | TABLES | SCOROUT |
| SimpleKappa | Simple kappa coefficient | TEST or EXACT | KAPPA KAPPA |
| SimpleKappaMC | Monte Carlo exact test for simple kappa | EXACT | KAPPA / MC |
| SimpleKappaTest | Simple kappa test | TEST or EXACT | KAPPA KAPPA |
| SomersDCR | Somers D ( C R ) | TEST | SMDCR |
| SomersDCRTest | Somers D ( C R ) test | TEST | SMDCR |
| SomersDRC | Somers D ( R C ) | TEST | SMDRC |
| SomersDRCTest | Somers D ( R C ) test | TEST | SMDRC |
| SpearmanCorr | Spearman correlation | TEST or EXACT | SCORR SCORR |
| SpearmanCorrMC | Monte Carlo exact test for Spearman correlation | EXACT | SCORR / MC |
| SpearmanCorrTest | Spearman correlation test | TEST or EXACT | SCORR SCORR |
| SymmetryTest | Test of symmetry | TABLES | AGREE |
| TauB | Kendall s tau- b | TEST | KENTB |
| TauBTest | Kendall s tau- b test | TEST | KENTB |
| TauC | Stuart s tau- c | TEST | STUTC |
| TauCTest | Stuart s tau- c test | TEST | STUTC |
| TrendTest | Cochran-Armitage test for trend | TABLES | TREND |
| TrendTestMC | Monte Carlo exact test for trend | EXACT | TREND / MC |
| WeightedKappa | Weighted kappa | TEST or EXACT | WTKAP WTKAP |
| WeightedKappaMC | Monte Carlo exact test for weighted kappa | EXACT | WTKAP / MC |
| WeightedKappaTest | Weighted kappa test | TEST or EXACT | WTKAP WTKAP |
EAN: 2147483647
Pages: 74
- Key #1: Delight Your Customers with Speed and Quality
- Key #4: Base Decisions on Data and Facts
- Beyond the Basics: The Five Laws of Lean Six Sigma
- Making Improvements That Last: An Illustrated Guide to DMAIC and the Lean Six Sigma Toolkit
- The Experience of Making Improvements: What Its Like to Work on Lean Six Sigma Projects