THE MULTIDIMENSIONAL AGGREGATE DATA STRUCTURE
|
|
In this section we will describe the data structure (simple, complex, and composite) of multidimensional aggregate data. First of all, we will discuss the important concept of dimension and the hierarchy concept, which is implicit in it.
As previously said, a measure of a MAD is described by a set of dimensions. These are, in reality, a set of category attributes (see, for example, Rafanelli, 1990); each of them can be a level of one of the possible hierarchies which form the primitive dimension. Each category attribute also has a primitive category attribute (several category attributes can have the same primitive category attribute), to which all the attributes with the same semantics are linked and whose domain consists of the union of all the domains of the category attributes previously linked to it. This is quite important when, for example, different category attributes linked to the primitive attribute have different names. For example, in one MADS the category attribute year appears and in another MADS the category attribute years appears. Therefore, they will be linked to the same primitive category attribute year, which semantically expresses the same concept. Thus, the primitive dimension is the union of all the primitive category attributes which refer to this dimension. These attributes are part of one or more hierarchies. For example, "province" could be one level of the hierarchy "political classification," which, together with the other hierarchies "health care zone classification" and "energy zone classification," form the unique dimension "geography," as shown in Figure 3. Note that the political classification considers province as partitioned into two different kinds of cities: small cities (town) and big cities (city). These last are also sub-divided into districts.
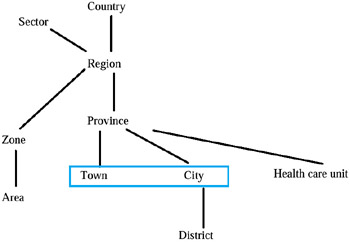
Figure 3: The "Geography" Primitive Dimension
Note also that this representation can assume the so-called "spider" configuration, in the sense that transversal hierarchies can generate different roots, so that the "all" term, as formulated in Gray et al. (1997), can also be lacking. With the term "primitive" we mean to express the concept of completeness regarding that dimension (in our case, geography), i.e., that such a dimension cannot assume other values (from the intentional point of view, other category attributes, from the extensional point of view, other instances of definition domain of each category attribute which defines every level) than those which appear in it. These and other concepts will be discussed in Chapter 4.
The complexity of aggregate data is also due to the fact that the same operator may require different recomputation functions for the summary values, depending on the summary type of the multidimensional aggregate table, as illustrated in Fortunato et al. (1986), and in Rafanelli & Ricci (1993). Summary data are always fixed in time, in the sense that every instance of the time dimension statically characterizes the measure described by it (and by the other category attributes which describe the numerical values that are in the table cells). It is always (implicitly or explicitly) present in every MAD. Another dimension always implicitly or explicitly present in every MAD is space. Shoshani (1982) wrote: "…the partitioning of geography can change with the application. In addition, the classification of the parameters can change over time." There followed an example in which problems without strict geographical hierarchies (for example, descendent elements not always fully contained within a single parent element) and changes over time (for example, definitions of regions changed over time due to legislative action or political needs or changes which evolve over time like the classification of diseases) underlay the research over the following years.
Subsequently, it was modeled on the fact that both time and space can be either implicit, in the sense that they might appear in the name of the table but not as descriptive variables, or explicit, as claimed by Bezenchek, Rafanelli, & Tininini (1996b). Virtually, using a 2-D representation requires squeezing the multi-dimensional space into two dimensions. This is usually done by choosing several of the dimensions to be represented as rows and several as columns. In general, the 2-D representation of multi-dimensional aggregate data forces a (possibly arbitrary) choice of two hierarchies for the rows and columns. The apparent conclusion is that a proper model should retain the concept of multi-dimensionality and represent it explicitly, as observed in Rafanelli & Shoshani (1990). In the 2-D representation, classification hierarchies are represented in the same manner as the multi-dimensional categories, while actually the classification hierarchy represents a single dimension. Consider, for example, the table "Employment in California" classified by "sex," "year," and by "professional categories"—"Professions" (the numbers are fictitious), taken from Rafanelli & Shoshani (1990) and shown in Figure 4.
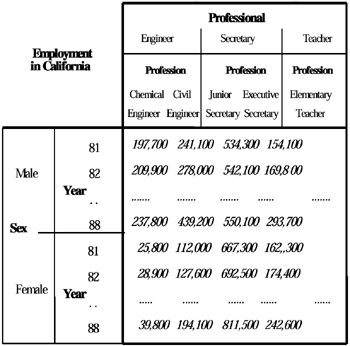
Figure 4: The 2-D Representation of a Multidimensional MADS
It is obvious from this example that the values of average income are given for specific combinations of "sex," "year," and "profession" only. Thus, "professional category" is not part of the multi-dimensional space of this statistical object, but part of a "hierarchical" classification relationship, "professional categories" → "professions" (where the notation → means a one-to-many relationship). This means that a hierarchical relationship exists between the instances of "professional class" (e.g., "engineer") and the instances of the "profession" (e.g., "civil engineer"), i.e., there is a fundamental difference between category structure and multi-dimensionality. Usually, only the low-level elements of the classification relationship participate in the multi-dimensional space. This fundamental difference should be explicitly represented in a semantically correct multidimensional aggregate data model. Moreover, by necessity, more than one dimension must be represented by the rows and the columns if more than two dimensions exist in the dataset. This is accomplished by selecting an arbitrary order of the dimensions for the rows and the columns, as noted in Shoshani (1997). The label "Employment in California" represents the summary measure for this table, but it also says that this table has an additional dimension "state" where the instance value selected is a singleton "California." Finally, there is a summary function implied (in this case it is "sum") with this table for further summarization to be done.
Another important characteristic of aggregate data, in contrast to conventional disaggregate data, is that they are essentially static. Only recently, with the increasing interest in developing business analysis and decision support applications, the on-line analysis of data (using sophisticated mathematical and statistical formulas, and consolidating summary data), such data have also assumed a dynamic connotation. But, even if the values change over time, it is usually necessary to record the evolution, rather than just the current version of the database, i.e., to add the new values without changing the old ones. For these reasons, the dimensions "time" and "space" (when and where the fact happens) have a particular importance in this kind of data. Different data structures, in the context of a data model, were proposed. For example, in Ozsoyoglu & Ozsoyoglu (1983) and, subsequently, in Ozsoyoglu, Ozsoyoglu, & Mata (1985), a summary table schema and a summary table instance were formally defined. In particular, a summary table schema S (Fr, Fc, C) is a three-tuple where Fr and Fc denote a row and column category attribute forest, and C is an ordered multi-set of cell attributes. In a summary table, a category attribute may be elementary or set-valued, but the cell attributes are always elementary. A summary table instance is a collection of cell instances structured as specified by the summary table schema.
In Rafanelli & Shoshani (1990), the Storm model is proposed. The authors speak explicitly of aggregate databases calling them statistical databases. Moreover, independently of the different, possible ways of representation (tables, relations, vectors, pies, bar-charts, graphs, and so on) of the structure stored in this database, such a structure is called a statistical object (SO). Each statistical object is characterized by having two different types of attributes: (a) a single summary attribute (that is, the result of the application of aggregate functions on microdata). A summary attribute has a summary type, which depends on the type of function applied to the microdata; and (b) a set of category attributes, which describe the summary attribute. therefore, the authors formally define a statistical object as in the following:
A Statistical Object is a data structure defined by a quadruple
<N, C, S, f>, where:
N is the name of the SO, which describes the universe of the phenomenon of interest (for example, "Average income in California").
C is a finite set of category attributes; each category attribute has a domain associated with it, and a "domain cardinality" which corresponds to the number of values (sometimes called "modalities" by statisticians) of its domain.
is a single summary attribute associated with the SO. The summary attribute has a domain and a domain cardinality associated with it.
f is a function which maps, from the cross-product of the category attribute values, to the summary attribute values of the SO.
By cross-product the authors mean the Cartesian product in which its member order has no importance (i.e., A x B x B × A). Each category attribute also has a primitive category attribute (several category attributes can have the same primitive category attribute), to which all the attributes with the same semantics are linked. Its domain also consists of the union of all the domains of the previous category attributes linked to it.
In the following we will propose the multidimensional aggregate data (MAD) and the multidimensional aggregate data structure (MADS), respectively the conceptual and logical structure of aggregate data.
|
|
EAN: 2147483647
Pages: 150