TWO-DIMENSIONAL TABLES

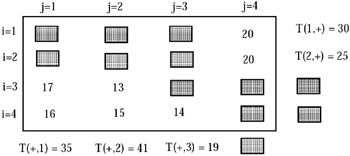
In this section we show how the data-map approach can be used to decide if an incomplete two-dimensional table (i.e., a table with suppressions) is or is not weakly safe. We shall consider the general case that primary and complementary suppressions are not limited to internal entries; thus, entries corresponding to row totals and column totals can also be suppressed (Kelly, Golden & Assad, 1992; Malvestuto & Moscarini, 1996a, 1996b; Chu, 1997). The following example is taken from Malvestuto & Moscarini (1996b), where the problem of testing weak safety is solved with an ad hoc method. Consider the following incomplete table and suppose that it was obtained from a complete table by suppressing the following entries:

We assume that T(i, j) is the value of a summary attribute a of nonnegative real type. Moreover, without loss of generality, we can suppose that i and j index the values of two descriptive attributes b′ and b′′, respectively with domains B′ = {b′[i]: i = 1, 2, 3, 4} and B′′ = {b′′[j]: j =1, 2, 3, 4}, which were used to categorize the individuals of the underlying population in the original complete table; thus, the category variable is b = (b′, b′′) and the domain of b is the Cartesian product B = B′ X B′′. Then, Table 6 can be thought of as being a set Q of 12 sum queries on a corresponding to its entries; for example, the category predicates of the sum queries on a with values T(1, 4), T(1, +), and T(+, 1) are respectively

Accordingly, the active domain of b with respect to Q is given by

and its characteristic partition g is the point partition. The data map of Q is then a weighted hypergraph (H, w) with 12 vertices (corresponding to the unsuppressed entries in Table 6)

and 14 edges labeled by the classes of γ. The edges of H contain one or two vertices; for example, the edge labeled by the class {(b′[3], b′′[3])} of γ contains exactly one vertex, the vertex (+, 3), and the edge labeled by the class {(b′[1], b′′[1])} γ of contains exactly two vertices, the vertices (1, +) and (+, 1). The data map of Q is shown in Figure 37 and the reduced data map of Q is the graph shown in Figure 38.

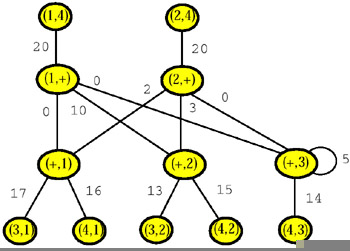
Figure 37

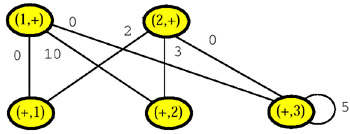
Figure 38

It should be noted that, generally speaking, the data map of the query set Q associated with an incomplete table need not be a graph, for if for some i and j none of the cells (i, j), (i, +), and (+, j) has been suppressed, then the data map of Q will contain the edge {(i, j), (i, +), (+, j)}. However, the reduced data map of Q is always a graph.

Before closing this section, we give the formal definition of the data map and the reduced data map of the query set Q associated with a given incomplete version of a complete table T. Let S be the set of suppressed internal cells, I the set of suppressed row totals, and J the set of suppressed column totals. The data map (H, w) of Q is defined as follows. The vertex set of H is taken to be

As for the edges of H, we proceed as follows. Let S′ = {(i, j) ∈ S: i ∈ I and j ∈ J}. Moreover, for each i ∉ I, let J_i = {j ∈ J: (i, j) ∈ S}; analogously, for each j ∉ J, let I_j = {i ∈ I: (i, j) ∈ S}. For example, for Table 6 one has J₁ = J₂ = Ø, and I₁ = I₂ = Ø and I₃ = {3}. Then the active domain of b with respect to Q is

and its characteristic partition γ contains

• one elementary class {(b′[i], b′′[j])} for each (i, j) ∉ S;

• one elementary class {(b′[i], b′′[j])} for each i and j such that (i, j) ∈ S and i ∉ I and j ∉ J;

• one class {(b′[i], b′′[j]): j ∈ J_i} for each i ∉ I with J_i ≠ Ø;

• one class {(b′[i], b′′[j]): i ∈ I_j} for each j ∉ J with I_j ≠ Ø.

The edge set of H is taken to be

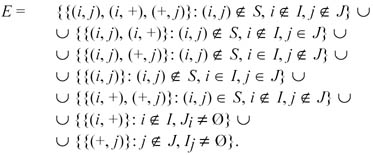
The labels and the weights of the edges e of H are reported below:

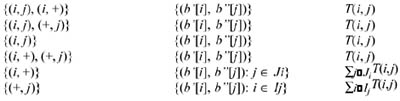
The reduced data map of Q is the graph with vertex set

and edge set