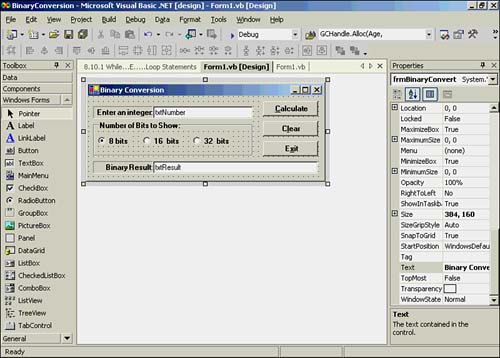
The BinaryConversion Program
| Let's write a program named BinaryConversion that uses a While loop. The various control objects are shown in Figure 13.1. Figure 13.1. The form and control objects for the BinaryConversion program. The three buttons are named btnCalc , btnClear , and btnExit . Inside a group box, I've also added three radio buttons named rbBits8, rbBIts16, and rbBits32. These radio buttons are used to select whether the binary number is display with 8, 16, or 32 bits. The Clear button is simply used to clear the txtNumber and txtResult text boxes. More Than Meets the EyeWhat isn't clear just by looking at Figure 13.1 is that the program is capable of converting either way. That is, if you type a decimal number into txtNumber and click the Calculate button, the binary representation of the number is shown in the txtResult text box. However, if the txtNumber text box is empty and you type a binary representation of a number into the txtResult text box and click Calculate, the decimal value for the binary number is shown in the txtNumber text box. This means the program can do decimal-to-binary or binary-to-decimal conversions. In other words, this program is actually useful! First, let's look at the btnCalc Click event code. This is shown in Listing 13.1. Listing 13.1 Code for the btnCalc Click EventPrivate Sub btnCalc_Click(ByVal sender As System.Object, ByVal e As _ System.EventArgs) Handles btnCalc.Click Dim number As Long, BitCount As Integer If rbBits8.Checked = True Then ' 8-bit result? BitCount = 8 Else If rbBits16.Checked = True Then ' Perhaps 16-bit? BitCount = 16 Else BitCount = 32 ' Must be 32-bit. End If End If If txtNumber.Text <> "" Then ' Did they enter a decimal number? number = CLng(txtNumber.Text) txtResult.Text = ConvertToBinary(number, BitCount) Else If txtResult.Text <> "" Then txtNumber.Text = ConvertToDecimal(txtResult.Text) End If End If End Sub The code defines two working variables and then does a series of If tests to determine whether the user wants the result displayed in a field of 8, 16, or 32 bits. Next , the code checks to see whether the txtNumber text box is empty. If the text box isn't empty, we assume the user wants to convert the number in the text box to binary. The code then calls the ConvertToBinary() function. The value returned is then displayed in the txtResult text box. If the txtNumber text box is empty, the code checks to see whether the user entered a binary number into txtResult . If so, the code calls the ConvertToDecimal() function. The value returned from the call is displayed in the txtNumber text box. It should be obvious that most of the work is done by the two functions that are called in the btnCalc Click event. Let's take a look at these two functions. The ConvertToBinary() FunctionThe code for the decimal-to-binary converter is shown in Listing 13.2. Listing 13.2 The Code for the Decimal-to-Binary FunctionPublic Function ConvertToBinary(ByVal number As Long, ByVal bits As _ Integer) As String ' Purpose: to convert a number into a string that is the ' binary representation of the number ' ' Parameters: ' number the decimal number to convert expressed as a long ' bits the number of bits to show ' ' Return value: ' string the binary representation of the number ' Dim Length As Integer Dim One As Integer, power As Long Dim bin As String Length = bits ' Save bit count While Length >= 0 power = 2 ^ Length One = CInt(number \ power) ' Divide number by appropriate power If One Then bin += "1" ' If big enough Else bin += "0" End If number = number Mod power ' Get the remainder Length -= 1 End While ' This keeps the result within the bit length ConvertToBinary = Microsoft.VisualBasic.Right(bin, bits) End Function First, notice that we comment the code so the reader can get an idea of what the function does. We do this because this particular function could be used by other programmers in other programs. After the function's documentation, several working variables are defined. The Length variable is set equal to bits . A While loop begins with a test on the number of bits passed to the function. The number of bits can be 8, 16, or 32, depending on which radio button the user selected. Notice that the While loop tests Length to see that it is greater than or equal to 0. If the user selects 8 bits, Length equals 8 and we enter the While loop. This code is a little tricky. Because we're going to allow 0 to be a valid condition for another iteration of the While loop, we'll have a total of nine passes through the loop. That's because we allow all positive numbers (that is, the 8 bits) plus the pass through the loop when Length is zero. An example will show why we do it this way. Suppose that the user selects 8 bits, but enters the number 256. The largest number that can be represented in 8 bits is 255. To show the binary value 256 would require 9 bits to display, or 100000000 The program statement near the end of Listing 13.2 ConvertToBinary = Microsoft.VisualBasic.Right(bin, bits) returns only the rightmost 8 bits of the string, or 00000000 . This is exactly what should be returned if the user selects 8 bits. If the user subsequently selects 16 bits, the number can be properly displayed. This also allows the program to work even if the user enters a number that's too large for the number of bits selected (within reasonable limits). Let's look at the code inside the While loop in Listing 13.2. Suppose the user enters 128 for the number and selects 8 bits. In the first statement, we have power = 2 ^ Length power = 2 ^ 8 power = 256 The next line then becomes One = CInt(128 \ 256) One = CInt(0) One = 0 Recall that integer division cannot have a fractional value, so 128 divided by 256 is 0. The If statement results in a 0 being assigned into bin . The next statement evaluates : number = number Mod power number = 128 Mod 256 number = 128 Because the Mod operator returns the remainder of integer division, 256 divides into 128 zero times with a remainder of 128. Therefore, number still equals 128. We then decrement Length from 8 to 7 and return back to the top of the While loop. Now let's evaluate the next three statements again: power = 2 ^ 7 power = 2 ^ 7 power = 128 The next line then becomes One = CInt(128 \ 128) One = CInt(1) One = 1 The If test now adds a 1 to bin , which now becomes 01 . Look what happens in the next statement: number = number Mod power number = 128 Mod 128 number = 0 If we divided 128 by 128, we get 1 with a remainder of 0. Because number is now 0, the statement near the top of the loop becomes One = CInt(0 \ power) for the rest of the passes through the While loop. You should be able to convince yourself that this will result in seven zeroes being concatenated to bin . Because bin is already equal to 01, when it finishes the loop, it will equal 010000000 The final statement at the bottom of the function ConvertToBinary = Microsoft.VisualBasic.Right(bin, bits) means that only the rightmost eight bits are returned, which becomes 10000000 . This is the binary value of 128. The ConvertToDecimal() FunctionThe ConvertToDecimal() function takes a binary number and converts it into a decimal number. The code is presented in Listing 13.3. Listing 13.3 The ConvertToDecimal() Function CodePublic Function ConvertToDecimal(ByVal bits As String) As String ' Purpose: to convert a binary number into a decimal number ' ' Parameters: ' bits the string of bits that is the binary number ' ' Return value: ' string the decimal representation of the binary number ' Dim i, Length As Integer Dim result As Long Length = bits.Length - 1 result = 0 i = 0 While Length >= 0 If bits.Substring(i, 1) = "1" Then result += 2 ^ Length End If Length -= 1 i += 1 End While ConvertToDecimal = CStr(result) End Function Let's suppose that the user presses the Clear button to remove whatever strings happen to be in the text boxes. Suppose the user types the string 101 into the txtResult text box. When the user clicks the Calculate button, the ConvertToDecimal() function is called. Length is assigned one less than the length of the string that holds the binary number. In our example, Length equals 2 . The code then sets result and i equal to and we enter the While loop. The statement If bits.Substring(i, 1) = "1" Then uses the Substring() method to examine a single character in the bits string. On the first pass through the loop, the value of i is , so we're looking at the first character in 101 , or the first 1 in the bits string. (Review Chapter 6, "String Variables," if you don't recall how the Substring() method works.) Therefore, because the If test is True, we enter the Then statement block. When we enter the Then statement block, the value of Length is 2 , so the statement result += 2 ^ Length becomes result += 2 ^ 2 result += 4 Because result was to begin with, result now equals 4 . Next, Length is decremented by 1 and variable i is incremented to 1. Program control then goes back up to the While statement. Because Length is still greater than or equal to 0, the relational test is True and we execute another pass through the loop. The Substring() method now examines the second character in the bits string, which is . The If test fails, and we again decrement Length and increment i . Control is again sent back to the top of the While loop. The Substring() method now examines the last character in the string, a 1 . Because the If test is True, we process the result statement. At this point, result equals 4 , so Result += 2 ^ 0 4 += 1 5 which is the value of result after the statement is executed. Length is decremented, i is incremented, and control goes back to the top of the While loop. However, Length now equals -1 , so Expression1 is logic False, and the While loop is not executed. The final statement in the function is executed and the string value of result (that is, 5) is passed back to the caller. Therefore, the binary number 101 is decimal 5. Taa-Daa it works! Save your work; these routines may be useful in other programs you write. (Keep in mind that we're experimenting with only positive numbers.) Experiment with different values and single-step through the code to see how the control of the program is affected by the While statements. |
EAN: 2147483647
Pages: 238