30.5 Going Further: Dependent Types

< Free Open Study >

Much of this book has been concerned with formalizing abstraction mechanisms of various sorts. In the simply typed lambda-calculus, we formalized the operation of taking a term and abstracting out a subterm, yielding a function that can later be instantiated by applying it to different terms. In System F, we considered the operation of taking a term and abstracting out a type, yielding a term that can be instantiated by applying it to various types. In λ_ω, we recapitulated the mechanisms of the simply typed lambda-calculus "one level up," taking a type and abstracting out a subexpression to obtain a type operator that can later be instantiated by applying it to different types.

A convenient way of thinking of all these forms of abstraction is in terms of families of expressions, indexed by other expressions. An ordinary lambda-abstraction λx:T₁.t₂ is a family of terms [x ↦ s]t₁ indexed by terms s. Similarly, a type abstraction λX::K₁.t₂ is a family of terms indexed by types, and a type operator is a family of types indexed by types.

λx:T₁.t₂

family of terms indexed by terms

λX::K₁.t₂

family of terms indexed by types

λX::K₁.T₂

family of types indexed by types.

Looking at this list, it is clear that there is one possibility that we have not considered yet: families of types indexed by terms. This form of abstraction has also been studied extensively, under the rubric of dependent types.

Dependent types offer a degree of precision in describing program behaviors that goes far beyond the other typing features we have seen. As a simple example of this, suppose we have a built-in type FloatList with the usual associated operations:

   nil     :  FloatList   cons    :  Float → FloatList → FloatList   hd      :  FloatList → Float   tl:     :  FloatList → FloatList   isnil   :  FloatList → Bool

In a language with dependent types, we can refine the simple type FloatList to a family of types FloatList n—the types of lists with n elements.

To take advantage of this refinement, we sharpen the types of the basic list operations. To begin with, we give the constant nil type FloatList 0. To give more accurate types to the rest of the operations, we need to refine the notation for function types to express the dependency between their arguments and the types of their results. For example, the type of cons should be roughly "a function that takes a Float and a list of length n and returns a list of length n+1." If we make the binding of n explicit by providing it as an initial argument, this description becomes "a function that takes a number n, a Float, and a list of length n, and returns a list of length succ n." That is, what we need to capture in the type is the dependency between the value of the first argument (n) and the types of the third argument (FloatList n) and the result (FloatList (succ n)). We accomplish this by binding a name to the first argument, writing Πn:Nat. ... instead of Nat→.... The types of cons and the other list operations then become

   nil    :  FloatList 0   cons   :  Πn:Nat. Float → FloatList n → FloatList (succ n)   hd     :  Πn:Nat. FloatList (succ n) → Float   tl     :  Πn:Nat. FloatList (succ n) → FloatList n.

The types of nil, cons, and tl tell us exactly how many elements are in their results, while hd and tl demand non-empty lists as arguments. Also, note that we don't need isnil any more, since we can tell whether an element of FloatList n is nil just by testing whether n is 0.

Dependent function types of the form Πx:T₁.T₂ are a more precise form of arrow types T₁→T₂, where we bind a variable x representing the function's argument so that we can mention it in the result type T₂. In the degenerate case, when T₂ does not mention x, we write Πx:T₁.T₂ as T₁→T₂.

Of course, we can also define new terms with dependent function types. For example, the function

   consthree = λn:Nat. λf:Float. λl:FloatList n.                  cons (succ(succ n)) f                    (cons (succ n) f                       (cons n f l));

which prepends three copies of its second argument (f) at the front of its third argument (⌉), has type

   Πn:Nat. Float → FloatList n → FloatList (succ(succ(succ n))).

Note that the first argument to each of the three calls to cons is different, reflecting the different lengths of their list arguments.

There is an extensive literature on dependent types in computer science and logic. Some good starting points are Smith, Nordström, and Petersson (1990), Thompson (1991), Luo (1994), and Hofmann (1997).

30.5.1 Exercise [⋆⋆]

Fixing the type of the elements of lists to be Float keeps the example simple, but we can generalize it to lists of an arbitrary type T using ordinary type operators. Show how to do this.

Continuing along the same lines, we can build higher-level list-manipulating functions with similarly refined types. For example, we can write a sorting function whose type,

   sort : Πn:Nat. FloatList n → FloatList n,

tells us that it returns a list of the same length as its input. Indeed, by further refining the type families involved, we can even write a sort function whose type tells us that the list it returns is always sorted. Checking that this sort function actually belongs to this type will then amount to proving that it meets its specification!

Such examples conjure up an alluring picture of a world in which programs are correct by construction, where a program's type tells us everything we want to know about its behavior and an "ok" from the typechecker gives us complete confidence that the program behaves as we expect. This vision is related to the idea of programming by "extracting the computational content" from a proof that a specification is satisfiable. The key observation is that a constructive proof of a theorem of the form "For every x there exists a y such that P" can be viewed as a function mapping x to y, together with some evidence (which is computationally inessential—i.e., of interest only to the typechecker) that this function has the property P. These ideas have been pursued by researchers in the Nuprl (Constable et al., 1986), LEGO (Luo and Pollack, 1992; Pollack, 1994) and Coq (Paulin-Mohring, 1989) projects, among others.

Unfortunately, the power of dependent types is a two-edged sword. Blurring the distinction between checking types and carrying out proofs of arbitrary theorems does not magically make theorem proving simple—on the contrary, it makes typechecking computationally intractable! Mathematicians working with mechanical proof assistants do not just type in a theorem, press a button, and sit back to wait for a Yes or No: they spend significant effort writing proof scripts and tactics to guide the tool in constructing and verifying a proof. If we carry the idea of correctness by construction to its limit, programmers should expect to expend similar amounts of effort annotating programs with hints and explanations to guide the typechecker. For certain critical programming tasks, this degree of effort may be justified, but for day-to-day programming it is almost certainly too costly.

Nonetheless, there have been several attempts to use dependent types in the design of practical programming languges, including Russell (Donahue and Demers, 1985; Hook, 1984), Cayenne (Augustsson, 1998), Dependent ML (Xi and Pfenning, 1998, 1999), Dependently Typed Assembly Language (Xi and Harper, 2001), and the shape types of Jay and Sekanina (1997). The trend in these languages is toward restricting the power of dependent types in various ways, obtaining more tractable systems, for which typechecking can be better automated. For example, in the languages of Xi et al., dependent types are used only for static elimination of run-time bounds checking on array accesses; the "theorem proving" problems generated during typechecking in these languages are just systems of linear constraints, for which good automatic procedures exist.

One area where dependent types have a long history of influence on programming languages is in the design of module systems that incorporate mechanisms for tracking sharing between inter-module dependencies. Land-marks in this area include Pebble (Burstall and Lampson, 1984), MacQueen (1986), Mitchell and Harper (1988), Harper et al. (1990), and Harper and Stone (2000). Recent papers in this area have adopted the technical device of singleton kinds, in which module dependency is tracked at the level of kinds instead of types (e.g., Stone and Harper, 2000; Crary, 2000; also see Hayashi, 1991; Aspinall, 1994).

The combination of dependent types with subtyping was first considered by Cardelli (1988b), and has been further developed and generalized by Aspinall (1994), Pfenning (1993b), Aspinall and Compagnoni (2001), Chen and Longo (1996), and Zwanenburg (1999).

Another important application of dependent types in computer science is in building proof assistants and automated theorem provers. In particular, simple type systems with dependent types are often called logical frameworks. The most famous of these is the pure simply typed calculus with dependent types, LF (Harper, Honsell, and Plotkin, 1992). LF and its relatives, in particular the calculus of constructions (Coquand and Huet, 1988; Luo, 1994), have formed the basis for a long line of theorem proving environments, including AutoMath (de Bruijn, 1980), NuPRL (Constable et al., 1986), LEGO (Luo and Pollack, 1992; Pollack, 1994), Coq (Barras et al., 1997), ALF (Magnusson and Nordström, 1994), and ELF (Pfenning, 1994). Pfenning (1996) surveys this area in more depth.

The four forms of abstraction discussed earlier in this section are neatly summarized by the following diagram, known as the Barendregt cube:^[3]

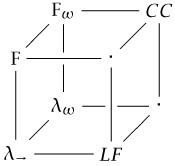
All the systems of the cube include ordinary term abstraction. The top face represents systems with polymorphism (families of terms indexed by types), the back face systems with type operators, and the right face systems with dependent types. In the far right corner is the calculus of constructions, containing all four forms of abstraction. The other corner that we have mentioned above is LF, the simply typed lambda-calculus with dependent types. All the systems of the Barendregt cube, and many others, can be presented as instances of the general framework of pure type systems (Terlouw, 1989; Berardi, 1988; Barendregt, 1991, 1992; Jutting, McKinna, and Pollack, 1994; McKinna and Pollack, 1993; Pollack, 1994).

^[3]Barendregt (1991) called it the lambda cube.

< Free Open Study >

λx:T₁.t₂	family of terms indexed by terms
λX::K₁.t₂	family of terms indexed by types
λX::K₁.T₂	family of types indexed by types.