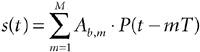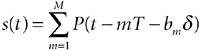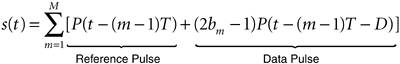Section 3.3. Pulse Modulation and Detection Techniques
3.3. Pulse Modulation and Detection Techniques3.3.1. On-Off KeyingOn-off keying (OOK) is the simplest form of pulse modulation, in which the transmission of a pulse represents a data bit 1 and its absence represents a data bit 0. Figure 3-3 shows an example of the OOK modulation technique in UWB communications systems. Figure 3-3. On-off keying modulation
The general signal model, s(t), for an OOK modulated signal can be represented by Equation 3-8
where M is the maximum number of transmitted bits, P(t) is the UWB pulse, bm OOK is a special case of pulse-amplitude modulation, and its main advantages are simplicity and low implementation cost. The OOK transmitter is quite uncomplicated; a simple RF switch can be turned on and off to represent data. This way, OOK modulation allows the transmitter to idle while transmitting a bit 0 and thus save power. The detection of OOK-modulated pulses is typically done with a noncoherent energy detector receiver, although CMF receivers can also be used. Despite the simplicity of OOK transmitters, this modulation scheme has several disadvantages in UWB systems. OOK is highly sensitive to noise and interference: an unwanted signal can be detected as a false data bit 1. Therefore, OOK is not a popular modulation technique for multiple-access communications channels. Also, the difficult task of UWB synchronization becomes even more challenging for OOK if a stream of zeros is transmitted. 3.3.2. Pulse-Amplitude ModulationPulse-amplitude modulation (PAM) encodes the data bits based on different levels of power (amplitude) in short-duration pulses. In this modulation technique, a pulse with higher amplitude represents a data bit 1 and a pulse with lower amplitude represents a data bit 0. Figure 3-4 shows an example of PAM for UWB communications. Figure 3-4. Pulse-amplitude modulation
The general signal model for PAM signals is given by Equation 3-9
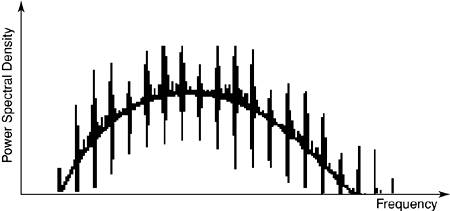
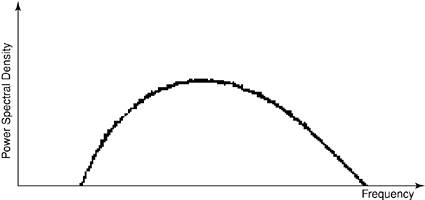
where Ab,m is the specific power level for each user's data bits, M is the maximum number of transmitted bits, P(t) is the UWB pulse, bm PAM generation is also simple, because it requires pulses with only one polarity to represent data. Pulses modulated with PAM can be detected with an energy detector receiver or a CMF receiver. Although PAM pulses are less sensitive to noise than OOK-modulated pulses, attenuation in wireless channels can convert them to the OOK case. Furthermore, because of the periodicity of transmitted pulses, some discrete lines will be present on the power spectral density (PSD) of PAM pulses. These discrete lines can cause harmful interference to other narrowband and wideband signals sharing the frequency spectrum with UWB systems. Figure 3-5 illustrates such discrete spectral lines on the PSD of periodic pulses. Figure 3-5. Discrete spectral lines of periodic pulses
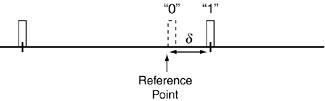
The discrete power spectral lines not only can cause harmful interference to conventional radio services, but they can also correlate with strong narrowband signals and cause interference to UWB signals. Therefore, it's quite important to avoid the discrete spectral lines by choosing the right modulation or special spectrum-whitening techniques. For more information on spectrum whitening, refer to [1, 2]. 3.3.3. Pulse-Position ModulationIn pulse-position modulation (PPM), signals are pseudorandomly encoded based on the position of the transmitted pulse trains by shifting the pulses in a predefined window in time. Compared to OOK and PAM pulses, PPM signals are more immune to false detection due to channel noise. This is because the pulses that represent the data bits in PPM have the same amplitude, so the probability of detecting a false data bit is reduced. A version of PPM represents a data bit 0 by no shift with respect to a specific reference point in time; it represents a data bit 1 by a pulse advancing the same reference point as shown in Figure 3-6. Figure 3-6. Pulse-position modulation
The general signal model for PPM signals is given by Equation 3-10
where d is the modulation index that provides a time shift to represent digital bits, M is the maximum number of transmitted bits, P(t) is the UWB pulse, bm Pulse-position modulated UWB signals are less sensitive to channel noise compared to PAM signals. However, they are vulnerable to catastrophic collisions that are caused by multiple-access channels. Note that the pseudorandom pulse positions alleviate the problem with discrete spectral lines in the PSD of a pulse modulated with the PPM scheme. Figure 3-7 represents an ideal case of smooth PSD generated by nonperiodic signals. Figure 3-7. An ideal smooth spectrum of nonperiodic pulses
PPM transmitted signals are usually demodulated and recovered with template matching or the CMF technique at the receiver. However, there is a major drawback to using CMF receivers for PPM, as well as for all the aforementioned UWB modulation techniques: CMF receivers work based on correlating the received UWB pulse with a predefined template pulse generated locally at the receiver. However, a weak and low-powered UWB pulse can be distorted so much by the transmission link that it shows little or no correlation with the clean template at the receiver. For this reason, reliable pulse detection with CMF receivers requires estimation of channel parameters, such as delay, attenuation, and fading, to provide templates that resemble the received pulse. Although channel estimation is a well-defined task in narrowband communications systems, it poses a major challenge in UWB links due to the extremely narrow pulses employed in these systems. Therefore, reliable detection of pulses becomes a major challenge in conventional pulse-detection techniques such as PPM. Another disadvantage of the PPM scheme is its sensitivity to timing synchronization. Because data bits are recovered exclusively based on their exact position in time, timing uncertainties, such as jitter and drift, can degrade their performance significantly. For instance, timing uncertainties can cause synchronization errors that result in increased MAI in multiple-access channels. Further, the strict timing synchronization of narrow UWB pulses prior to the correlation process in PPM receivers requires very fast (on the order of gigahertz) analog-to-digital converters (ADCs). Moreover, multipath distortions can stretch the pulses and cause them to overlap; thus detection becomes challenging based on the prior knowledge of the pulse positions in PPM systems. 3.3.4. Biphase ModulationIn biphase modulation, the polarity of the pulse changes to represent digital data bits. For instance, a pulse with positive polarity represents a digital bit 1, where a pulse with negative polarity corresponds to a bit 0. Figure 3-8 demonstrates biphase modulation for UWB pulses. Figure 3-8. Biphase modulation
The general signal model for biphase modulation is given by Equation 3-11
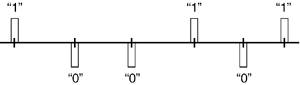
where M is the maximum number of transmitted bits, P(t) is the UWB pulse, bm This type of modulation scheme is less susceptible to distortion because the difference between the two pulse levels is twice the pulse amplitude. Another advantage of biphase modulation is that the change in polarity can remove the discrete spectral lines in the pulse's PSD, because changing the polarity of pulses produces a zero mean [3]. However, this modulation scheme results in more complexity in the physical implementation of the transmitter: It requires one transmitter to generate positive pulses and another transmitter to generate negative pulses. Moreover, for a stream of data, accurate timing between the two transmitters is of great importance. 3.3.5. Transmitted-Reference ModulationTransmitted-reference modulation has been envisioned since the 1920s for synchronizing spread-spectrum communications systems [3]. This technique was reintroduced in the field of ultra-wideband communications recently [see 47] for its simplicity, robust performance in multipath channels, and avoidance of the stringent synchronization requirements of conventional pulse-detection techniques. Because of the advantages that TR modulation offers over the previously defined modulation schemes, it has been playing an increasingly important role in UWB communications lately. Therefore, in this section, we pay special attention to TR modulation and explain it in more detail. TR modulation is defined as the transmission of a pair of pulses or doublets separated in time. The first pulse in a TR doublet is the reference pulse. This pulse is unmodulated and does not carry any information. After a certain time interval D, the reference pulse is followed by a data-modulated pulse, known as the data pulse or the transmit pulse. As with the previously described modulation schemes, individual pulses in the waveform can be any variety of wideband pulses, such as Gaussian, chirp, or Hermite-based narrow pulses. Data is modulated based on the relative polarity of the reference and data pulses. For instance, a reference and a data pulse of the same polarity designate a binary value of 1, while a data pulse opposite in polarity to the reference pulse corresponds to a binary value of 0, as shown in Figure 3-9. Figure 3-9. Transmitted-reference pulse modulation. (a) The symbol for data bit 1. (b) The symbol for data bit 0.
The general signal model for a TR modulated pulse is Equation 3-12
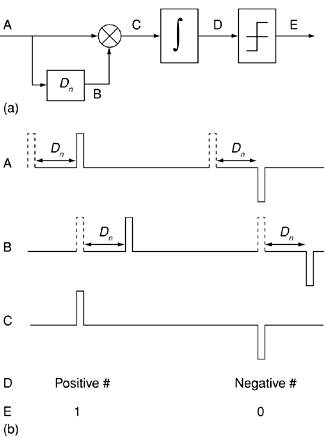
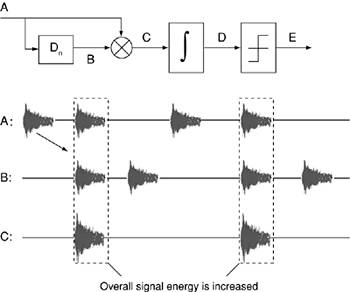
where M is the maximum number of transmitted bits, P(t) is the UWB pulse, bm Like a CMF receiver, a TR receiver uses the correlation scheme, but with one major distinction. Instead of correlating the received pulses with a predefined, "clean" template, which has not experienced any channel distortions, a TR receiver correlates the received signal with a delayed version of itself. This way each reference pulse acts as a template for its subsequent data pulse. Therefore, the spacing between the reference and data pulses, D, plays a crucial role in recovering data at the receiver. Figure 3-10 shows the block diagram of a TR receiver, followed by a simple example of TR demodulation. Figure 3-10. (a) Block diagram of a TR receiver. (b) An example of TR demodulation. Dotted lines represent reference pulses, and solid lines represent data pulses.
As shown in Figure 3-10, the TR receiver forms a product of the received signal with its delayed version. Delaying the received signal by D units in time causes the reference pulse to align with the data pulse in each symbol. This product generates positive and negative values that are then translated to binary 1 or 0 by a hard decision device. An important advantage of the TR modulation technique is that it sends the same pulse twice through an unknown channel. Both pulses experience the same type of channel distortion, and thus detection with a correlation receiver becomes easier. Therefore, instead of correlating the distorted received pulse with a clean template pulse as in PPM, the TR receiver correlates the similarly distorted data pulse and reference pulse, which show high correlation. Therefore, in TR receivers there is no need for channel estimation algorithms. Further, a TR receiver is self-synchronized, which eliminates the need for individual pulse synchronization with locally generated templates, as in PPM. Each reference pulse acts as a preamble for its data pulse, providing rapid synchronization. Moreover, sampling in TR receivers occurs after correlation between the data pulses and the reference pulses; thus the sampling requirements are relaxed to baseband signals. This way, the need for synchronization of the received narrow RF pulses and very fast ADCs is eliminated. Another advantage of TR modulation over the other UWB modulation schemes is its high performance in multipath environments. TR receivers exploit the multipath phenomenon to improve their performance in dense multipath and indoor channels. This is because the reference and data pulses are correlated with each other, and the multipath channel introduces a longer duration in the signal component of the received signal, thus increasing the overall signal energy at the output of the integrator, as shown in Figure 3-11. Figure 3-11. Transmitted-reference demodulation in the presence of multipath channels
As shown in Figure 3-11, the multipath channel has the same stretching effect on both the reference and the data pulses. Therefore, high correlation between these two pulses exists, and at stage C in the figure we see the increase in the integration time that corresponds to an increase in the overall signal energy. In this case, the integration period should be adjusted to capture most of the multipath energy, which usually results from the strong reflected signals that exist in delay spread.[2] In other words, the strong multipath components in the received signal contain significant energy, and the ability to capture that energy by correlating the received signal and its delayed version is quite important in low-power UWB communications systems. For PPM or PAM receivers to achieve performance similar to that of TR receivers in multipath channels, additional rake receivers[3] with a large number of fingers would be required, which would significantly increase the system complexity.
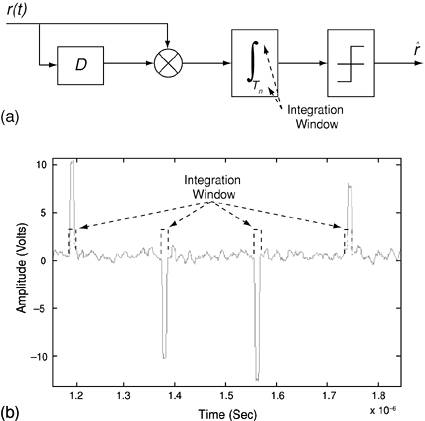
Despite all of its advantages, TR modulation suffers from a major drawback associated with the correlation of noise on noise caused by the overlap of reference and data pulses. Therefore, the performance of these receivers is considerably limited by the severity of the noise-on-noise component introduced by various types of channel noise, such as AWGN or NBI [9]. It is expected that TR receivers will perform poorly at links with a low SNR, or in the presence of strong narrowband interferers. Techniques for mitigating the interference to TR receivers are available in [7, 10]. Another drawback of TR modulation is that for every data bit, two pulses must be transmitted. Transmitting a reference pulse with every data pulse dilutes the transmitter power and reduces the data rate. Also, the periodicity in TR receivers can cause undesired discrete spectral lines on the PSD of a TR-modulated UWB pulse. This undesired characteristic can be improved by staggering the pulse transmission from a periodic one and still take advantage of TR benefits for UWB communications. Furthermore, although TR receivers ease the strict synchronization requirement in UWB systems, their performance largely depends on the appropriate use of their integration window in the presence of channel noise. The integration window defines the limits of the finite integrator prior to the final decision-making block. Figure 3-12 represents the integration window in TR receivers. Figure 3-12. The integration window in (a) TR receivers and in (b) the received signal in a noisy LOS channel
The integration window introduces two important design parameters: length of integration interval and accurate position of the integration interval. The length of integration window plays a major role in the performance of UWB-TR receivers in both LOS and NLOS channels. In LOS channels, if this window is smaller than the pulse width, only a fraction of pulse energy is collected, introducing more degradation than the gain achieved by the decrease in noise. This results in a net decrease of the output SNR. Similarly, if the integration window is larger than the pulse width, a larger amount of noise is introduced to the integrator. Hence, noise energy builds up, with no additional signal energy, and causes a decrease in output SNR. Consequently, the length of the integration window should be equal to the pulse width in LOS channels to capture most of the pulse energy. The optimal length of an integration window in multipath channels is studied in [9, 11]. Figure 3-13 illustrates the importance of integration window length in UWB-TR receivers. Figure 3-13. A UWB signal and variations of the integration window's length in TR receivers
As shown in Figure 3-13, the first window on the left is too narrow to capture the total signal energy. The window in the middle is too wide, and it introduces more noise into the system. Finally, the window on the right has the proper length to capture the signal energy without introducing additional noise. Accurate timing of the acquisition and tracking of the integration window for each received bit is another important factor in the performance of UWB-TR receivers. Any deviation from the precise position of this window causes a decrease in the SNR of the received signal and results in the false detection of data bits and severe performance degradation of the receiver. Figure 3-14 shows the importance of the integration window's position in UWB-TR receivers. Figure 3-14. A UWB signal and variations of the integration window's position in TR receivers
As shown in Figure 3-14, although we are using the proper length for the integration window (from the previous example in Figure 3-13), the receiver can still suffer from significant performance degradation due to the integration window's improper position. The first and second windows from the left capture only parts of the signal energy. The third window just captures noise, with no signal content. The last window on the right, thanks to its precise position, is the only one that captures the entire signal energy. |
EAN: 2147483647
Pages: 93
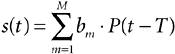
 [0,1] represents the
[0,1] represents the