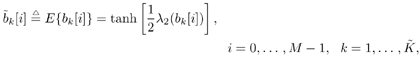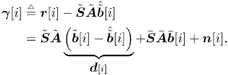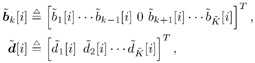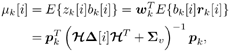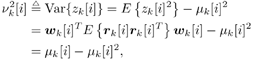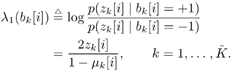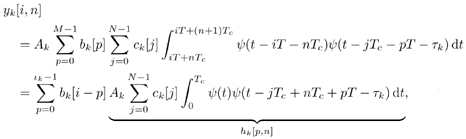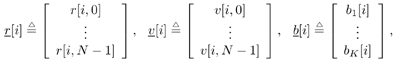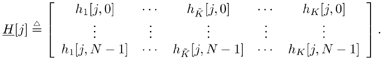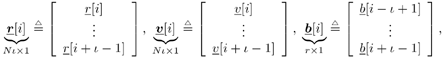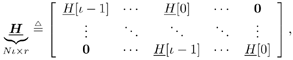6.4 Turbo Multiuser Detection with Unknown Interferers
| The turbo multiuser detection techniques developed so far assume that the spreading waveforms of all users are known to the receiver. Another important scenario, discussed in Chapter 3, is that the receiver has knowledge of the spreading waveforms of some but not all of the users in a system. Such a situation arises, for example, in a cellular system where the base station receiver knows the spreading waveforms of the in-cell users but not those of the out-of- cell users. In this section we discuss a turbo multiuser detection method that can be applied in the presence of unknown interference, which was first developed in [414]. 6.4.1 Signal Model Consider again the synchronous CDMA signal model (6.27). Here we assume that the spreading waveforms and the received amplitudes of the first Equation 6.72 The resulting discrete-time signal corresponding to the i th symbol is then given by Equation 6.73 Equation 6.74 with where Equation 6.75 is a Gaussian random variable; n [ i ] ~ N ( , s 2 I N ); s k is the normalized discrete-time spreading waveform of the k th user , with c n,k Denote by Equation 6.76 Since we do not have knowledge of Equation 6.77 where 6.4.2 Group -Blind SISO Multiuser DetectorThe heart of the turbo group-blind receiver is the soft-input/soft-output (SISO) group-blind multiuser detector. The detector accepts, as inputs, the a priori LLRs for the code bits of the known users delivered by the SISO MAP channel decoders of these users, and produces, as outputs, updated LLRs for these code bits. This is accomplished by soft interference cancellation and MMSE filtering. Specifically, using the a priori LLRs and knowledge of the signature sequences and received amplitudes of the known users, the detector performs a soft-interference cancellation for each user, in which estimates of the multiuser interference from the other known users and an estimate for the interference caused by the unknown users are subtracted from the received signal. Residual interference is suppressed by passing the resulting signal through an instantaneous MMSE filter. The a posteriori LLR can then be computed from the MMSE filter output. The detector first forms soft estimates of the user code bits as Equation 6.78 where l 2 ( b k [ i ]) is the a priori LLR of the k th user's i th bit delivered by the MAP channel decoder. We denote hard estimates of the code bits as Equation 6.79 and denote In the next step we form an estimate of interference of the unknown users, I [ i ], which we denote by Equation 6.80 where Equation 6.81 It will be seen that our ability to form a soft estimate for d k [ i ] will allow us to perform the soft interference cancellation mentioned above. Clearly, d k [ i ] can take on one of two values, 0 or 2 b k [ i ]. The probability that d k [ i ] is equal to zero is the probability that the hard estimate is correct and is given by Equation 6.82 Recall that for b Equation 6.83 On substituting b = sign {tanh [ ½ l 2 ( b k )[ i ]} in (6.83), we find that Equation 6.84 Therefore, d k [ i ] is a random variable that can be described as Equation 6.85 We now perform an eigendecomposition on G G T / M where Equation 6.86 Denote Equation 6.87 Now we subtract the interference estimate from the received signal and form a new signal Equation 6.88 where Equation 6.89 with Equation 6.90 For each known user we perform a soft interference cancellation on z [ i ] to obtain Equation 6.91 where with Equation 6.92 Substituting (6.88) into (6.91), we obtain Equation 6.93 An instantaneous linear MMSE filter is then applied to r k [ i ] to obtain Equation 6.94 The filter Equation 6.95 where the expectation is with respect to the ambient noise and the interfering users. The solution to (6.95) is given by Equation 6.96 It is easy to show that Equation 6.97 where Equation 6.98 The diagonal elements of D 11 [ i ] are given by Equation 6.99 Using (6.85), the diagonal elements of D 22 [ i ] are given by Equation 6.100 where Equation 6.101 The diagonal elements of D 12 [ i ] and D 21 [ i ] are identical and are given by Equation 6.102 It is also easy to see that Equation 6.103 where e k is a Equation 6.104 As before, we make the assumption that the MMSE filter output is Gaussian; we may write Equation 6.105 where m k [ i ] is the equivalent amplitude of the k th user's signal at the filter output, and h k [ i ] ~ N (0, Equation 6.106 Equation 6.107 where (6.107) follows from (6.97), (6.104), and (6.106). Finally, exactly the same as (6.64), the extrinsic information, l 1 ( b k [ i ]), delivered by the SISO multiuser detector is given by Equation 6.108 This group-blind SISO multiuser detection algorithm is summarized as follows. Algorithm 6.3: [Group-blind SISO multiuser detector ”synchronous CDMA]
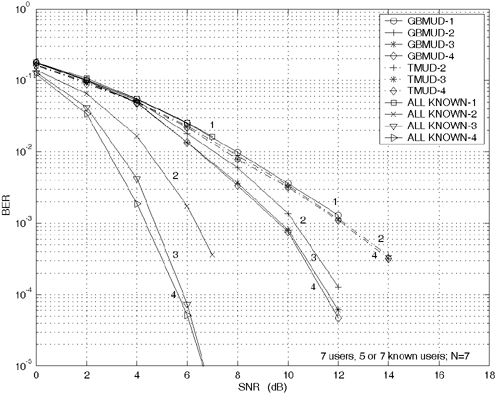
6.4.3 Sliding Window Group-Blind Detector for Asynchronous CDMA It is not difficult to extend the results of Section 6.4.2 to asynchronous CDMA. The received signal due to user k (1 Equation 6.119 where t k is the delay of the k th user's signal, { c j,k } Equation 6.120 is match-filtered to the chip waveform and sampled at the chip rate. The n th matched-filter output during the i th symbol interval is Equation 6.121 Substituting (6.119) into (6.121), we obtain Equation 6.122 where Equation 6.123 Denote Equation 6.124 and for j = 0, 1, ..., I k “1, Equation 6.125 Then Equation 6.126 By stacking Equation 6.127 Equation 6.128 where Equation 6.129 Define the set of matrices Equation 6.130 This equation is the asynchronous analog to (6.76). We can obtain estimates of Simulation ExamplesWe next present simulation results to demonstrate the performance of the proposed turbo group-blind multiuser receiver for asynchronous CDMA. The processing gain of the system is seven and the total number of users is seven. The number of known users is either two or five, as noted on the figures. The spreading sequences are randomly generated and the same sequences are used for all simulations. All users employ the same rate- ½, constraint-length-3 convolutional code (with generators g 1 = [110] and g 2 = [111]). Each user uses a different random interleaver, and the same interleavers are used in all simulations. The block size of information bits for each user is 128. The maximum delay in symbol intervals is 1. All users use the same transmitted power and the chip pulse waveform is a raised cosine with roll-off factor 0.5. Figure 6.11 illustrates the average bit-error-rate performance of the known users for the group-blind turbo receiver and the conventional turbo receiver discussed in Section 6.3 for the first four iterations. The number of known users is five. For the sake of comparison, we have included plots for the conventional turbo receiver when all of the users are known. The three sets of plots in this figure are denoted in the legend by "GBMUD," "TMUD," and "ALL KNOWN," respectively. Note that the curves for the first iteration are identical for GBMUD and TMUD. Hence we have suppressed the plot of the first iteration for TMUD, to improve clarity. Notice that iteration does not significantly improve the performance of the conventional turbo receiver, whereas the group-blind receiver provides significant gains through iteration at moderate and high signal-to-noise ratios. We can also see that the use of more than three iterations does not provide significant benefits. Figure 6.11. Performance of a group-blind iterative multiuser receiver with five known users. Curves denoted GBMUD are produced using a turbo group-blind multiuser receiver and those denoted TMUD are produced using a standard turbo multiuser receiver. Also included are plots for TMUD when all users are known. In Fig. 6.12, the number of known users has been changed to two. As we would expect, there is performance degradation for both conventional and group-blind turbo receivers. In fact, the conventional receiver gains nothing through iteration for this scenario because there are now five users whose interference is simply ignored. It is also apparent that the group-blind turbo receiver will not be able to mitigate all of the interference of unknown users, even for a large number of iterations. This is due, in part, to the use of an imperfect interference subspace estimate in the SISO group-blind multiuser detector. Figure 6.12. Performance of a group-blind iterative multiuser receiver with two known users. Curves denoted GBMUD are produced using a turbo group-blind multiuser receiver and those denoted TMUD are produced using a standard turbo multiuser receiver. Also included are plots for TMUD when all users are known. |
EAN: 2147483647
Pages: 91
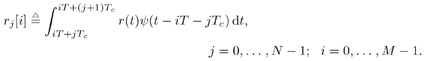
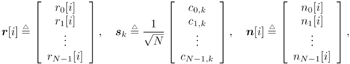
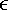 {+1, “1};
{+1, “1};