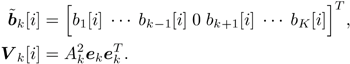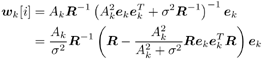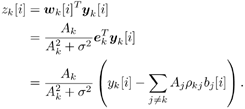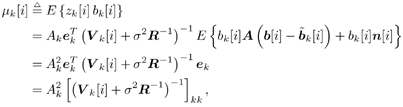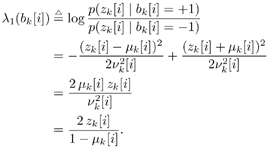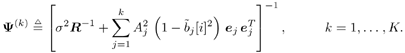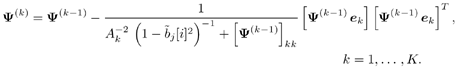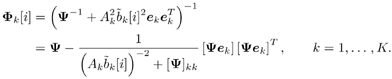6.3 Turbo Multiuser Detection for Synchronous CDMA
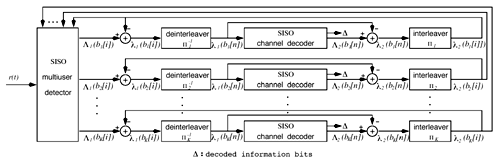
6.3.1 Turbo Multiuser ReceiverWe consider a convolutionally coded synchronous real-valued CDMA system with k users, employing normalized modulation waveforms s 1 , s 2 , ..., s k , and signaling through an additive white Gaussian noise channel. A block diagram of the transmitter end of such a system is shown in Fig. 6.4. The binary information symbols { d k [ m ]} m for user k , k = 1, ..., K, are convolutionally encoded with code rate R k . A code-bit interleaver is used to reduce the influence of the error bursts at the input of each channel decoder. The interleaved code bits of the k th user are BPSK modulated, yielding data symbols of duration T . Each data symbol b k [ i ] is then spread by a signature waveform s k (t) and transmitted through the channel. Figure 6.4. Coded CDMA system. As seen from preceding chapters, the received continuous-time signal can be written as Equation 6.27 where n(t) is a zero-mean white Gaussian noise process with power spectral density s 2 and A k is the amplitude of the k th user. The turbo receiver structure is shown in Fig. 6.5. It consists of two stages: a soft-input/soft-output (SISO) multiuser detector, followed by k parallel single-user MAP channel decoders. The two stages are separated by deinterleavers and interleavers. The SISO multiuser detector delivers the a posteriori log- likelihood ratio (LLR) of a transmitted "+1" and a transmitted " “1" for every code bit of each user, Figure 6.5. Turbo multiuser receiver. Equation 6.28 As before, using Bayes' formula, (6.28) can be written as Equation 6.29 where the second term in (6.29), denoted by l 2 [ b k ( i )], represents the a priori LLR of the code bit b k [ i ], which is computed by the MAP channel decoder of the k th user in the previous iteration, interleaved and then fed back to the SISO multiuser detector. For the first iteration, assuming equally likely code bits (i.e., no prior information available), we then have l 2 ( b k [ i ]) = 0, for 1 Based on the prior information { l 1 ( Equation 6.30 where the second equality was shown in Section 6.2 [cf. (6.10)]. It is seen from (6.30) that the output of the MAP channel decoder is the sum of the prior information l 1 ( 6.3.2 Optimal SISO Multiuser DetectorFor the synchronous CDMA system (6.27), it is easily seen that a sufficient statistic for demodulating the i th code bits of the k users is given by the K -vector y [ i ] = [ y 1 [ i ] ... y K [ i ] T , whose k th component is the output of a filter matched to s k (.) in the i th code-bit interval: Equation 6.31 This sufficient statistic vector y [ i ] can be written as [520] Equation 6.32 where R denotes the normalized cross-correlation matrix of the signal set s 1 , ..., s K : Equation 6.33 In what follows , for notational simplicity, we drop the symbol index i whenever possible. Denote From (6.32), the extrinsic information l 1 ( b k ) delivered by the SISO multiuser detector [cf. (6.29)] is then given by Equation 6.34 where we have used the notation Equation 6.35 Note that the first term in (6.35) is independent of b and therefore will be canceled in (6.34). The third term in (6.35) can be written as Equation 6.36 Equation 6.37 where (6.36) follows from the fact that b j after some manipulations, we have for b j Equation 6.38 Equation 6.39 where (6.38) follows from a derivation similar to that of (6.37). Substituting (6.35), (6.37), and (6.39) into (6.34), we obtain Equation 6.40 It is seen from (6.40) that the extrinsic information l 1 ( b k [ i ]) at the output of the SISO multiuser detector consists of two parts ; the first term contains the channel value of the desired user y k [ i ]}, and the second term is the information extracted from the other users' channel values { y j [ i ]} j 6.3.3 Low-Complexity SISO Multiuser DetectorIt is clear from (6.40) that the computational complexity of the optimal SISO multiuser detector is exponential in terms of the number of users K, which is certainly prohibitive for channels with moderate to large numbers of users. In what follows we describe a low-complexity SISO multiuser detector based on a novel technique of combined soft interference cancellation and linear MMSE filtering, which was first developed in [552]. Soft Interference Cancellation and Instantaneous Linear MMSE FilteringBased on the a priori LLR of the code bits of all users, { l 2 ( b k [ i ])} k , provided by the MAP channel decoder from the previous iteration, we first form soft estimates of the code bits of all users as Equation 6.41 Equation 6.42 where (6.41) follows from (6.39). Define Equation 6.43 Equation 6.44 where e k denotes a K -vector of all zeros, except for the k th element, which is 1. Therefore, Equation 6.45 Such a soft interference cancellation scheme was first proposed in [168]. Next, in order to further suppress the residual interference in y k [ i ], an instantaneous linear minimum mean-square error (MMSE) filter w k [ i ] is applied to y k [ i ], to obtain Equation 6.46 where the filter Equation 6.47 where using (6.45), we have Equation 6.48 Equation 6.49 and in (6.48), Equation 6.50 because Equation 6.51 Denote Equation 6.52 Substituting (6.48) and (6.49) into (6.47), we have Equation 6.53 Substituting (6.45) and (6.53) into (6.46), we obtain Equation 6.54 Notice that the term R -1 y [ i ] in (6.54) is the output of a linear decorrelating multiuser detector. Next, we consider some special cases of the output z k [ i ].
Gaussian Approximation of Linear MMSE Filter OutputIt is shown in [386] that the distribution of the residual interference plus noise at the output of a linear MMSE multiuser detector is well approximated by a Gaussian distribution. In what follows, we assume that the output z k [ i ] of the instantaneous linear MMSE filter in (6.46) represents the output of an equivalent additive white Gaussian noise channel having b k [ i ] as its input symbol. This equivalent channel can be represented as Equation 6.61 where m k [ i ] is the equivalent amplitude of the k th user's signal at the output and h k [ i ] ~ N (0, Equation 6.62 Equation 6.63 Using (6.61) and (6.63) the extrinsic information delivered by the instantaneous linear MMSE filter is then Equation 6.64 Recursive Procedure for Computing Soft OutputIt is seen from (6.64) that to form the extrinsic LLR l 1 ( b k [ i ]) at the instantaneous linear MMSE filter, we must first compute z k [ i ] and m k [ i ]. From (6.54) and (6.62) the computation of z k [ i ] and m k [ i ] involves inverting a K x K matrix: Equation 6.65 Next we outline a recursive procedure for computing F k [ i ]. Define Equation 6.66 Using the matrix inversion lemma, Y ( k ) can be computed recursively as Equation 6.67 Denote Equation 6.68 Finally, we summarize the low-complexity SISO multiuser detection algorithm as follows. Algorithm 6.2: [Low-complexity SISO multiuser detector ”synchronous CDMA]
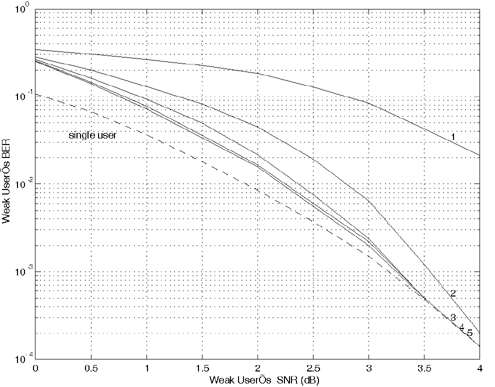
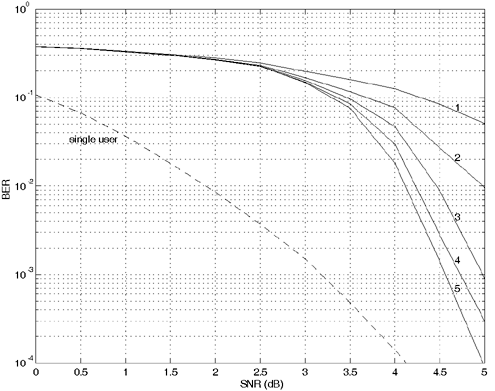
Equation 6.69 Equation 6.70 Equation 6.71 Next we examine the computational complexity of the low-complexity SISO multiuser detector discussed in this section. From the discussion above, it is seen that at each symbol time i , the dominant computation involved in computing the matrix Note that a number of studies have addressed different aspects of turbo multiuser detection in CDMA systems. In particular, in [336], an optimal turbo multiuser detector is derived based on iterative techniques for cross-entropy minimization. Turbo multiuser detection methods based on different interference cancellation schemes are proposed in [13, 14, 88, 129, 157, 200, 265, 397, 409, 410, 471, 552, 576, 608]. An interesting framework that unifies these approaches to iterative multiuser detection is given in [50]. Moreover, techniques for turbo multiuser detection in unknown channels are developed in [540, 593], which are based on the Markov chain Monte Carlo (MCMC) method for Bayesian computation. Application of the low-complexity SISO detection scheme discussed in this section to equalization of ISI channels with long memory is given in [413]. Simulation ExamplesIn this section we present some simulation examples to illustrate the performance of the turbo multiuser receiver in synchronous CDMA systems. Of particular interest is the receiver that employs the low-complexity SISO multiuser detector of the preceding section. All users employ the same rate- ½ constraint-length n = 5 convolutional code (with generators 23 and 35 in octal notation). Each user uses a different interleaver generated randomly . The same set of interleavers is used for all simulations. The block size of the information bits for each user is 128. First we consider a four-user system with equal cross- correlations r ij = 0.7, for 1 Figure 6.6. Performance of a turbo multiuser receiver that employs an optimal SISO multiuser detector. k = 4, r ij = 0.7. All users have equal power. Figure 6.7. Performance of a turbo multiuser receiver that employs a low-complexity SISO multiuser detector. k = 4, r ij = 0.7. All users have equal power. Figure 6.8. Strong user performance under a turbo multiuser receiver that employs a low-complexity SISO multiuser detector. k = 4, r ij = 0.7. Two users are 3 dB stronger than the other two. Figure 6.9. Weak user performance under a turbo multiuser receiver that employs a low-complexity SISO multiuser detector. k = 4, r ij = 0.7. Two users are 3 dB stronger than the other two. Figure 6.10. Performance of a turbo multiuser receiver that employs a low-complexity SISO multiuser detector. k = 8, r ij = 0.7. All users have equal power. |
EAN: 2147483647
Pages: 91


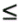
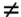
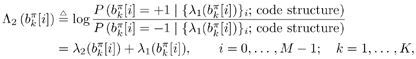
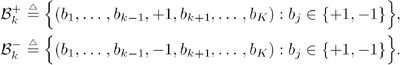
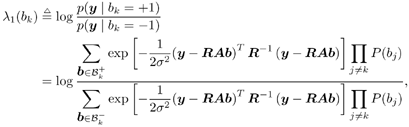
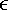 {+1, “1}. The summations in the numerator (respectively, denominator) in (6.34) are over all the 2 K-1 possible vectors
{+1, “1}. The summations in the numerator (respectively, denominator) in (6.34) are over all the 2 K-1 possible vectors 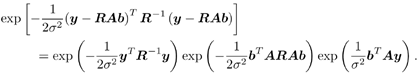
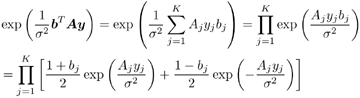
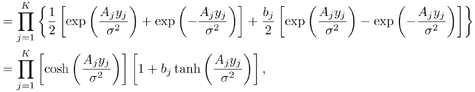
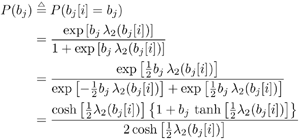
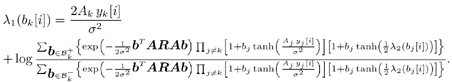

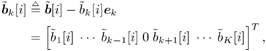
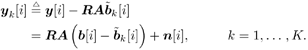
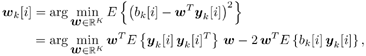
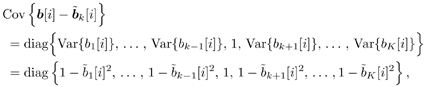
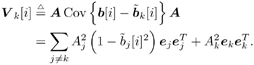
 for 1
for 1