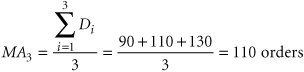Time Series Methods
Time Series MethodsTime series methods are statistical techniques that make use of historical data accumulated over a period of time. Time series methods assume that what has occurred in the past will continue to occur in the future. As the name time series suggests, these methods relate the forecast to only one factor time . Time series methods tend to be most useful for short-range forecasting, although they can be used for longer-range forecasting. We will discuss two types of time series methods: the moving average and exponential smoothing . Moving AverageA time series forecast can be as simple as using demand in the current period to predict demand in the next period. For example, if demand is 100 units this week, the forecast for next week's demand would be 100 units; if demand turned out to be 90 units instead, then the following week's demand would be 90 units, and so forth. This is sometimes referred to as na ve forecasting. However, this type of forecasting method does not take into account any type of historical demand behavior; it relies only on demand in the current period. As such, it reacts directly to the normal, random up-and-down movements in demand. Alternatively, the moving average method uses several values during the recent past to develop a forecast. This tends to dampen , or smooth out , the random increases and decreases of a forecast that uses only one period. As such, the simple moving average is particularly useful for forecasting items that are relatively stable and do not display any pronounced behavior, such as a trend or seasonal pattern. The moving average method is good for stable demand with no pronounced behavioral patterns . Moving averages are computed for specific periods, such as 3 months or 5 months, depending on how much the forecaster desires to smooth the data. The longer the moving average period, the smoother it will be. The formula for computing the simple moving average is as follows : where n = number of periods in the moving average D i = data in period i To demonstrate the moving average forecasting method, we will use an example. The Instant Paper Clip Supply Company sells and delivers office supplies to various companies, schools , and agencies within a 30-mile radius of its warehouse. The office supply business is extremely competitive, and the ability to deliver orders promptly is an important factor in gettting new customers and keeping old ones. (Offices typically order not when their inventory of supplies is getting low but when they completely run out. As a result, they need their orders immediately.) The manager of the company wants to be certain that enough drivers and delivery vehicles are available so that orders can be delivered promptly. Therefore, the manager wants to be able to forecast the number of orders that will occur during the next month (i.e., to forecast the demand for deliveries). From records of delivery orders, the manager has accumulated data for the past 10 months. These data are shown in Table 15.1. Table 15.1. Orders for 10-month period
The moving average forecast is computed by dividing the sum of the values of the forecast variable, orders per month for a sequence of months, by the number of months in the sequence. Frequently, a moving average is calculated for three or five time periods. The forecast resulting from either the 3- or the 5-month moving average is typically for the next month in the sequence, which in this case is November. The moving average is computed from the demand for orders for the last 3 months in the sequence, according to the following formula: The 5-month moving average is computed from the last 5 months of demand data, as follows: The 3- and 5-month moving averages for all the months of demand data are shown in Table 15.2. Notice that we have computed forecasts for all the months. Actually, only the forecast for November, based on the most recent monthly demand, would be used by the manager. However, the earlier forecasts for prior months allow us to compare the forecast with actual demand to see how accurate the forecasting method is (i.e., how well it does). Table 15.2. 3- and 5-month averages
Both moving average forecasts in Table 15.2 tend to smooth out the variability occurring in the actual data. This smoothing effect can be observed in Figure 15.2, in which the 3-month and 5-month averages have been superimposed on a graph of the original data. The extremes in the actual orders per month have been reduced. This is beneficial if these extremes simply reflect random fluctuations in orders per month because our moving average forecast will not be strongly influenced by them. Figure 15.2. 3- and 5-month moving averages(This item is displayed on page 672 in the print version) Notice that the 5-month moving average in Figure 15.2 smooths out fluctuations to a greater extent than the 3-month moving average. However, the 3-month average more closely reflects the most recent data available to the office supply manager. (The 5-month average forecast considers data all the way back to June; the 3-month average does so only to August.) In general, forecasts computed using the longer-period moving average are slower to react to recent changes in demand than those made using shorter-period moving averages. The extra periods of data dampen the speed with which the forecast responds. Establishing the appropriate number of periods to use in a moving average forecast often requires some amount of trial-and-error experimentation. Longer-period moving averages react more slowly to recent demand changes than do shorter-period moving averages . One additional point to mention relates to the period of the forecast. Sometimes a forecaster will need to forecast for a short planning horizon rather than just a single period. For both the 3- and 5-month moving average forecasts computed in Table 15.2, the final forecast is for one period only in the future. Because the moving average includes multiple periods of data for each forecast, and it is most often used to forecast in a stable demand environment, it would be appropriate to use the forecast for multiple periods in the future. It could then be updated as actual demand data became available. The major disadvantage of the moving average method is that it does not react well to variations that occur for a reason, such as trends and seasonal effects (although this method does reflect trends to a moderate extent). Those factors that cause changes are generally ignored. It is basically a "mechanical" method, which reflects historical data in a consistent fashion. However, the moving average method does have the advantage of being easy to use, quick, and relatively inexpensive, although moving averages for a substantial number of periods for many different items can result in the accumulation and storage of a large amount of data. In general, this method can provide a good forecast for the short run, but an attempt should not be made to push the forecast too far into the distant future. Weighted Moving AverageThe moving average method can be adjusted to reflect more closely more recent fluctuations in the data and seasonal effects. This adjusted method is referred to as a weighted moving average method. In this method, weights are assigned to the most recent data according to the following formula: where
In a weighted moving average , weights are assigned to the most recent data . For example, if the Instant Paper Clip Supply Company wants to compute a 3-month weighted moving average with a weight of 50% for the October data, a weight of 33% for the September data, and a weight of 17% for August, it is computed as Notice that the forecast includes a fractional part, .4. Because .4 order would be impossible , this appears to be unrealistic . In general, the fractional parts need to be included in the computation to achieve mathematical accuracy, but when the final forecast is achieved, it must be rounded up or down.
Also notice that this forecast is slightly lower than our previously computed 3-month average forecast of 110 orders, reflecting the lower number of orders in October (the most recent month in the sequence). Determining the precise weights to use for each period of data frequently requires some trial-and-error experimentation, as does determining the exact number of periods to include in the moving average. If the most recent months are weighted too heavily, the forecast might overreact to a random fluctuation in orders; if they are weighted too lightly, the forecast might underreact to an actual change in the pattern of orders. Exponential SmoothingThe exponential smoothing forecast method is an averaging method that weights the most recent past data more strongly than more distant past data. Thus, the forecast will react more strongly to immediate changes in the data. This is very useful if the recent changes in the data are the results of an actual change (e.g., a seasonal pattern) instead of just random fluctuations (for which a simple moving average forecast would suffice). Exponential smoothing is an averaging method that reacts more strongly to recent changes in demand than to more distant past data . We will consider two forms of exponential smoothing: simple exponential smoothing and adjusted exponential smoothing (adjusted for trends, seasonal patterns, etc.). We will discuss the simple exponential smoothing case first, followed by the adjusted form. To demonstrate simple exponential smoothing, we will return to the Instant Paper Clip Supply Company example. The simple exponential smoothing forecast is computed by using the formula F t +1 = a D t + (1 a ) F t where
The smoothing constant, a , is between zero and one. It reflects the weight given to the most recent demand data. For example, if a = .20, F t +1 = .20 D t + .80 F t which means that our forecast for the next period is based on 20% of recent demand ( D t ) and 80% of past demand (in the form of the forecast F t because F t is derived from previous demands and forecasts). If we go to one extreme and let a = 0.0, then and the forecast for the next period is the same as for this period. In other words, the forecast does not reflect the most recent demand at all . On the other hand, if a = 1.0, then The closer a is to one, the greater the reaction to the most recent demand . and we have considered only the most recent occurrence in our data (demand in the present period) and nothing else. Thus, we can conclude that the higher a is, the more sensitive the forecast will be to changes in recent demand. Alternatively, the closer a is to zero, the greater will be the dampening or smoothing effect. As a approaches zero, the forecast will react and adjust more slowly to differences between the actual demand and the forecasted demand. The most commonly used values of a are in the range from .01 to .50. However, the determination of a is usually judgmental and subjective and will often be based on trial-and-error experimentation. An inaccurate estimate of a can limit the usefulness of this forecasting technique. To demonstrate the computation of an exponentially smoothed forecast, we will use an example. PM Computer Services assembles customized personal computers from generic parts. The company was formed and is operated by two part-time State University students, Paulette Tyler and Maureen Becker, and has had steady growth since it started. The company assembles computers mostly at night, using other part-time students as labor. Paulette and Maureen purchase generic computer parts in volume at a discount from a variety of sources whenever they see a good deal. It is therefore important that they develop a good forecast of demand for their computers so that they will know how many computer component parts to purchase and stock. The company has accumulated the demand data in Table 15.3 for its computers for the past 12 months, from which it wants to compute exponential smoothing forecasts, using smoothing constants ( a ) equal to .30 and .50. Table 15.3. Demand for personal computers
To develop the series of forecasts for the data in Table 15.3, we will start with period 1 (January) and compute the forecast for period 2 (February) by using a = .30. The formula for exponential smoothing also requires a forecast for period 1, which we do not have, so we will use the demand for period 1 as both demand and the forecast for period 1 . Other ways to determine a starting forecast include averaging the first three or four periods and making a subjective estimate. Thus, the forecast for February is F 2 = a D 1 + (1 a ) F 1 = (.30)(37) + (.70)(37) = 37 units The forecast for period 3 is computed similarly: F 3 = a D 2 + (1 a ) F 2 = (.30)(40) + (.70)(37) = 37.9 units The remaining monthly forecasts are shown in Table 15.4. The final forecast is for period 13, January, and is the forecast of interest to PM Computer Services: F 13 = a D 12 + (1 a ) F 12 = (.30)(54) + (.70)(50.84) = 51.79 units Table 15.4 also includes the forecast values by using a = .50. Both exponential smoothing forecasts are shown in Figure 15.3, together with the actual data. Figure 15.3. Exponential smoothing forecasts Table 15.4. Exponential smoothing forecasts, a = .30 and a = .50
In Figure 15.3, the forecast using the higher smoothing constant, a = .50, reacts more strongly to changes in demand than does the forecast with a = .30, although both smooth out the random fluctuations in the forecast. Notice that both forecasts lag behind the actual demand. For example, a pronounced downward change in demand in July is not reflected in the forecast until August. If these changes mark a change in trend (i.e., a long- term upward or downward movement) rather than just a random fluctuation, then the forecast will always lag behind this trend. We can see a general upward trend in delivered orders throughout the year. Both forecasts tend to be consistently lower than the actual demand; that is, the forecasts lag behind the trend. Based on simple observation of the two forecasts in Figure 15.3, a = .50 seems to be the more accurate of the two, in the sense that it seems to follow the actual data more closely. (Later in this chapter we will discuss several quantitative methods for determining forecast accuracy.) In general, when demand is relatively stable, without any trend, using a small value for a is more appropriate to simply smooth out the forecast. Alternatively, when actual demand displays an increasing (or decreasing ) trend, as is the case in Figure 15.3, a larger value of a is generally better. It will react more quickly to the more recent upward or downward movements in the actual data. In some approaches to exponential smoothing, the accuracy of the forecast is monitored in terms of the difference between the actual values and the forecasted values. If these differences become larger, then a is changed (higher or lower) in an attempt to adapt the forecast to the actual data. However, the exponential smoothing forecast can also be adjusted for the effects of a trend. As we noted with the moving average forecast, the forecaster sometimes needs a forecast for more than one period into the future. In our PM Computer Services example, the final forecast computed was for 1 month, January. A forecast for 2 or 3 months could have been computed by grouping the demand data into the required number of periods and then using these values in the exponential smoothing computations . For example, if a 3-month forecast were needed, demand for January, February, and March could be summed and used to compute the forecast for the next 3-month period, and so on, until a final 3-month forecast resulted. Alternatively, if a trend were present, the final period forecast could be used for an extended forecast by adjusting it by a trend factor. Adjusted Exponential SmoothingThe adjusted exponential smoothing forecast consists of the exponential smoothing forecast with a trend adjustment factor added to it. The formula for the adjusted forecast is Adjusted exponential smoothing is the exponential smoothing forecast with an adjustment for a trend added to it . AF t +1 = F t +1 + T t +1 where T = an exponentially smoothed trend factor The trend factor is computed much the same as the exponentially smoothed forecast. It is, in effect, a forecast model for trend: T t +1 = b ( F t +1 - F t ) + (1 - b ) T t where T t = the last period trend factor b = a smoothing constant for trend Like a , b is a value between zero and one. It reflects the weight given to the most recent trend data. Also like a , b is often determined subjectively, based on the judgment of the forecaster. A high b reflects trend changes more than a low b . It is not uncommon for b to equal a in this method. The closer b is to one, the stronger a trend is reflected . Notice that this formula for the trend factor reflects a weighted measure of the increase (or decrease) between the current forecast, F t + 1 , and the previous forecast, F t . As an example, PM Computer Services now wants to develop an adjusted exponentially smoothed forecast, using the same 12 months of demand shown in Table 15.3. It will use the exponentially smoothed forecast with a = .50 computed in Table 15.4 with a smoothing constant for trend, b , of .30. The formula for the adjusted exponential smoothing forecast requires an initial value for T t to start the computational process. This initial trend factor is most often an estimate determined subjectively or based on past data by the forecaster. In this case, because we have a relatively long sequence of demand data (i.e., 12 months), we will start with the trend, T t , equal to zero. By the time the forecast value of interest, F 13 , is computed, we should have a relatively good value for the trend factor. The adjusted forecast for February, AF 2 , is the same as the exponentially smoothed forecast because the trend computing factor will be zero (i.e., F 1 and F 2 are the same and T 2 = 0). Thus, we will compute the adjusted forecast for March, AF 3 , as follows, starting with the determination of the trend factor, T 3 : T 3 = b ( F 3 F 2 ) + (1 b ) T 2 = (.30)(38.5 37.0) + (.70)(0) = 0.45 and AF 3 = F 3 + T 3 = 38.5 + 0.45 = 38.95 This adjusted forecast value for period 3 is shown in Table 15.5, with all other adjusted forecast values for the 12-month period plus the forecast for period 13, computed as follows: T 13 = b ( F 13 F 12 ) + (1 b ) T 12 = (.30)(53.61 53.21) + (.70)(1.77) = 1.36 and AF 13 = F 13 + T 13 = 53.61 + 1.36 = 54.96 units Table 15.5. Adjusted exponentially smoothed forecast values
The adjusted exponentially smoothed forecast values shown in Table 15.5 are compared with the exponentially smoothed forecast values and the actual data in Figure 15.4. Figure 15.4. Adjusted, exponentially smoothed forecast(This item is displayed on page 679 in the print version) Notice that the adjusted forecast is consistently higher than the exponentially smoothed forecast and is thus more reflective of the generally increasing trend of the actual data. However, in general, the pattern, or degree of smoothing, is very similar for both forecasts. Linear Trend LineLinear regression is most often thought of as a causal method of forecasting in which a mathematical relationship is developed between demand and some other factor that causes demand behavior. However, when demand displays an obvious trend over time, a least squares regression line, or linear trend line , can be used to forecast demand. A linear trend line is a linear regression model that relates demand to time .
A linear trend line relates a dependent variable, which for our purposes is demand, to one independent variable, time, in the form of a linear equation, as follows: y = a + bx where a = intercept (at period 0) b = slope of the line x = the time period y = forecast for demand for period x These parameters of the linear trend line can be calculated by using the least squares formulas for linear regression: As an example, consider the demand data for PM Computer Services shown in Table 15.3. They appear to follow an increasing linear trend. As such, the company wants to compute a linear trend line as an alternative to the exponential smoothing and adjusted exponential smoothing forecasts shown in Tables 15.4 and 15.5. The values that are required for the least squares calculations are shown in Table 15.6. Table 15.6. Least squares calculations
Using these values for Therefore, the linear trend line is y = 35.2 + 1.72 x To calculate a forecast for period 13, x = 13 would be substituted in the linear trend line: y = 35.2 + 1.72(13) = 57.56 Figure 15.5 shows the linear trend line in comparison to the actual data. The trend line visibly appears to closely reflect the actual data (i.e., to be a "good fit") and would thus be a good forecast model for this problem. However, a disadvantage of the linear trend line is that it will not adjust to a change in the trend as the exponential smoothing forecast methods will (i.e., it is assumed that all future forecasts will follow a straight line). This limits the use of this method to a shorter time frame in which the forecaster is relatively certain that the trend will not change. Figure 15.5. Linear trend line A linear trend line will not adjust to a change in trend as will exponential smoothing . Seasonal AdjustmentsAs we mentioned at the beginning of this chapter, a seasonal pattern is a repetitive up-and-down movement in demand. Many demand items exhibit seasonal behavior. Clothing sales follow annual seasonal patterns, with demand for warm clothes increasing in the fall and winter and declining in the spring and summer, as the demand for cooler clothing increases. Demand for many retail itemsincluding toys, sports equipment, clothing, electronic appliances, hams, turkeys, wine, and fruitincreases during the Christmas season. Greeting card demand increases in conjunction with various special days, such as Valentine's Day and Mother's Day. Seasonal patterns can also occur on a monthly, weekly, or even daily basis. Some restaurants have higher demand in the evening than at lunch, or on weekends as opposed to weekdays. Traffic and sales picks up at shopping malls on Friday and Saturday. There are several methods available for reflecting seasonal patterns in a time series forecast. We will describe one of the simpler methodsusing a seasonal factor , which is a numerical value that is multiplied by the normal forecast to get a seasonally adjusted forecast. It is possible to adjust for seasonality by multiplying the normal forecast by a seasonal factor . One method for developing a demand for seasonal factors is dividing the actual demand for each seasonal period by the total annual demand, according to the following formula: The resulting seasonal factors between zero and one are, in effect, the portion of total annual demand assigned to each season. These seasonal factors are thus multiplied by the annual forecasted demand to yield seasonally adjusted forecasts for each period. As an example, Wishbone Farms is a company that raises turkeys, which it sells to a meat-processing company throughout the year. However, the peak season obviously occurs during the fourth quarter of the year, October to December. Wishbone Farms has experienced a demand for turkeys for the past 3 years as shown in Table 15.7. Table 15.7. Demand for turkeys at Wishbone Farms
Because we have 3 years of demand data, we can compute the seasonal factors by dividing total quarterly demand for the 3 years by total demand across all 3 years: Next, we want to multiply the forecasted demand for the next year, 2006, by each of the seasonal factors to get the forecasted demand for each quarter. However, to accomplish this, we need a demand forecast for 2006. In this case, because the demand data in Table 15.7 seem to exhibit a generally increasing trend, we compute a linear trend line for the 3 years of data in Table 15.7 to use as a rough forecast estimate: y = 40.97 + 4.30 x = 40.97 + 4.30(4) = 58.17 Thus, the forecast for 2006 is 58.17, or 58,170 turkeys. Using this annual forecast of demand, the seasonally adjusted forecasts, SF i , for 2006 are as follows: SF 1 = ( S 1 )( F 5 ) = (.28)(58.17) = 16.28 SF 2 = ( S 2 )( F 5 ) = (.20)(58.17) = 11.63 SF 3 = ( S 3 )( F 5 ) = (.15)(58.17) = 8.73 SF 4 = ( S 4 )( F 5 ) = (.37)(58.17) = 21.53 Comparing these quarterly forecasts with the actual demand values in Table 15.7 shows them to be relatively good forecast estimates, reflecting both the seasonal variations in the data and the general upward trend.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 358