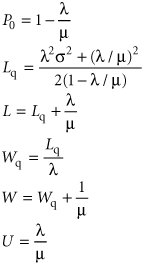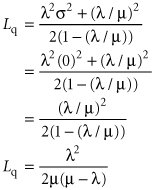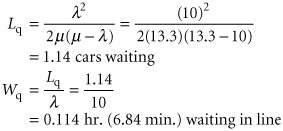Undefined and Constant Service Times
| Sometimes it cannot be assumed that a waiting line system has an arrival rate that is Poisson distributed or service times that are exponentially distributed. For example, many manufacturing operations use automated equipment or robots that have constant service times. Thus, the single-server model with Poisson arrivals and constant service times is a queuing variation that is of particular interest to manufacturing operations. Constant service times occur with machinery and automated equipment . Constant service times are a special case of the single-server model with undefined service times . The constant service time model is actually a special case of a more general variation of the single-server model in which service times cannot be assumed to be exponentially distributed. As such, service times are said to be general , or undefined . The basic queuing formulas for the operating characteristics of the undefined service time model are as follows : The key formula for undefined service times is for L q , the number of customers in the waiting line. In this formula, µ and s are the mean and standard deviation, respectively, for any general probability distribution with independent service times. For the Poisson distribution, the mean is equal to the variance. This same relationship is true for Poisson service rates if service times are exponentially distributed. Thus, if we let s = µ in the preceding formula for L q for undefined service times, it becomes the same as our basic formula with exponential service times. In fact, all the queuing formulas become the same as in the basic single-server model. As an example of the single-server model with undefined service times, consider a business firm with a single fax machine. Employees arrive randomly to use the fax machine, at an average rate of 20 per hour , according to a Poisson distribution. The time an employee spends using the machine is not defined by any probability distribution but has a mean of 2 minutes and a standard deviation of 4 minutes. The operating characteristics for this system are computed as follows: In the constant service time model, there is no variability in service times; s = 0 . In the case of constant service times, there is no variability in service times (i.e., service time is the same constant value for each customer); thus, s = 0. Substituting s = 0 into the undefined service time formula for L q results in the following formula for L q with constant service times: Notice that this new formula for L q for constant service times is simply our basic single-server formula for L q divided by two. All the remaining formulas for L , W q , and W are the same as the single-server formulas using this formula for L q . The following example illustrates the single-server model with constant service times. The Petroco Service Station has an automatic car wash, and motorists purchasing gas at the station receive a discounted car wash, depending on the number of gallons of gas they buy. The car wash can accommodate one car at a time, and it requires a constant time of 4.5 minutes for a wash. Cars arrive at the car wash at an average rate of 10 per hour (Poisson distributed). The service station manager wants to determine the average length of the waiting line and the average waiting time at the car wash. First, determine l and µ such that they are expressed as rates: l = 10 cars per hr. µ = 60/4.5 = 13.3 cars per hr. Substituting l and µ into the queuing formulas for constant service time, Computer Solution of the Constant Service Time Model with ExcelExhibit 13.4 shows an Excel spreadsheet set up to solve our Petroco Service Station example with constant service times. As in Exhibit 13.1 for the Fast Shop Market example, the queuing formulas are embedded in individual cells . For example, the formula for L q , the average number in the queue, is entered in cell D6 and is shown on the formula bar at the top of the spreadsheet. Exhibit 13.4.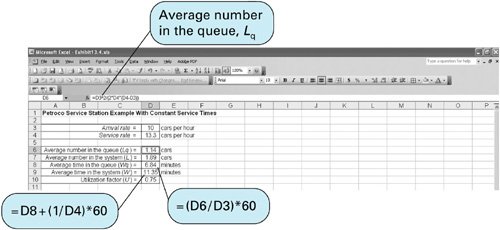 Computer Solution of the Undefined and Constant Service Time Models with QM for WindowsQM for Windows can be used to solve the single-server model with undefined (referred to as "general") and constant service times similarly to the single-server model in the previous section. Exhibit 13.5 shows the QM for Windows solution output screen for our fax machine example with undefined service times (on page 585). Exhibit 13.5.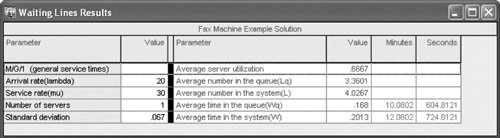 |
EAN: 2147483647
Pages: 358