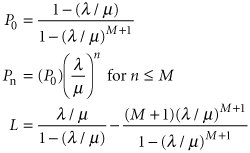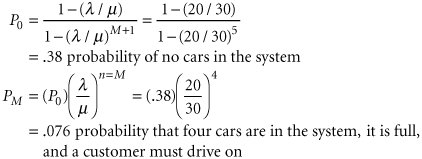Finite Queue Length
| For some waiting line systems, the length of the queue may be limited by the physical area in which the queue forms; space may permit only a limited number of customers to enter the queue. Such a waiting line is referred to as a finite queue and results in another variation of the single-phase , single-channel queuing model. In a finite queue , the length of the queue is limited . The basic single-server model must be modified to consider the finite queuing system. It should be noted that for this case, the service rate does not have to exceed the arrival rate ( µ > l ) in order to obtain steady-state conditions. The resulting operating characteristics, where M is the maximum number in the system, are as follows : Because P n is the probability of n units in the system, if we define M as the maximum number allowed in the system, then P M (the value of P n for n = M ) is the probability that a customer will not join the system. The remaining equations are As an example of the single-server model with finite queue, consider Metro Quick Lube, a one-bay service facility located next to a busy highway in an urban area. The facility has space for only one vehicle in service and three vehicles lined up to wait for service. There is no space for cars to line up on the busy adjacent highway , so if the waiting line is full (three cars), prospective customers must drive on. The mean time between arrivals for customers seeking lubrication service is 3 minutes. The mean time required to perform the lube operation is 2 minutes. Both the interarrival times and the service times are exponentially distributed. As stated previously, the maximum number of vehicles in the system is four. The operating characteristics are computed as follows: l = 20 µ = 30 M = 4 First, we will compute the probability that the system is full and the customer must drive on, P M . However, this first requires the determination of P , as follows: Next, to compute the average queue length, L q , the average number of cars in the system, L , must be computed, as follows:
To compute the average waiting time, W q , the average time in the system, W , must be computed first: Computer Solution of the Finite Queue Model with ExcelThe Excel spreadsheet solution to the Metro Quick Lube example problem with a finite queue is shown in Exhibit 13.6. Notice that the formula for P in cell D7 is shown on the formula bar at the top of the spreadsheet. The formula for L in cell D9 is shown in the callout box. Exhibit 13.6.(This item is displayed on page 590 in the print version)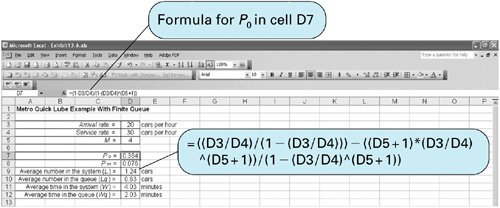 Note that Excel QM also has a spreadsheet macro for the finite queue model that can be accessed similarly to the single-server model in Exhibit 13.2. Computer Solution of the Finite Queue Model with QM for WindowsThe single-server model with finite queue can be solved with QM for Windows. Exhibit 13.7 shows the model solution screen for our Metro Quick Lube example. Exhibit 13.7.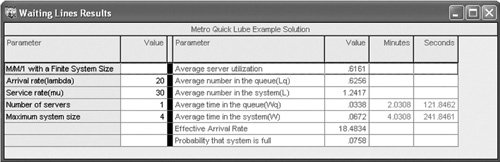 |
EAN: 2147483647
Pages: 358