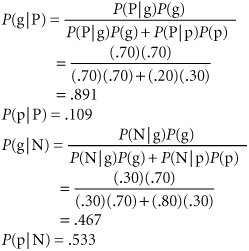Example Problem Solution

[Page 547 ( continued )]

The following example will illustrate the solution procedure for a decision analysis problem.

Problem Statement

T. Bone Puckett, a corporate raider, has acquired a textile company and is contemplating the future of one of its major plants, located in South Carolina. Three alternative decisions are being considered : (1) expand the plant and produce lightweight, durable materials for possible sales to the military, a market with little foreign competition; (2) maintain the status quo at the plant, continuing production of textile goods that are subject to heavy foreign competition; or (3) sell the plant now. If one of the first two alternatives is chosen , the plant will still be sold at the end of a year. The amount of profit that could be earned by selling the plant in a year depends on foreign market conditions, including the status of a trade embargo bill in Congress. The following payoff table describes this decision situation:

---

[Page 548]

	State of Nature
Decision	Good Foreign Competitive Conditions	Poor Foreign Competitive Conditions
Expand	$ 800,000	$ 500,000
Maintain status quo	1,300,000	150,000
Sell now	320,000	320,000

1. Determine the best decision by using the following decision criteria:

   1. Maximax

   2. Maximin

   3. Minimax regret

   4. Hurwicz ( a = .3)

   5. Equal likelihood

2. Assume that it is now possible to estimate a probability of .70 that good foreign competitive conditions will exist and a probability of .30 that poor conditions will exist. Determine the best decision by using expected value and expected opportunity loss.

3. Compute the expected value of perfect information.

4. Develop a decision tree, with expected values at the probability nodes.

5. T. Bone Puckett has hired a consulting firm to provide a report on future political and market situations. The report will be positive (P) or negative (N), indicating either a good (g) or poor (p) future foreign competitive situation. The conditional probability of each report outcome, given each state of nature, is

   P (Pg) = .70

   P (Ng) = .30

   P (Pp) = .20

   P (Np) = .80

   Determine the posterior probabilities by using Bayes's rule.

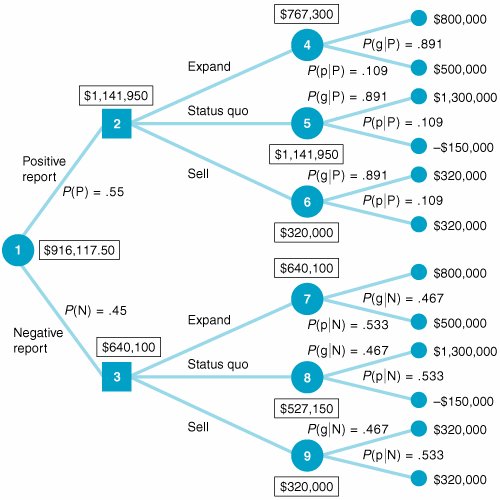
6. Perform a decision tree analysis by using the posterior probability obtained in (e).

Solution

Step  1.

(part A): Determine Decisions Without Probabilities

Maximax:
Expand	$ 800,000
Status quo	1,300,000	Maximum
Sell	320,000

Decision: Maintain status quo.

---

[Page 549]

Maximin:
Expand	$ 500,000	Maximum
Status quo	-150,000
Sell	320,000

Decision: Expand.

Minimax regret:
Expand	$500,000	Minimum
Status quo	650,000
Sell	980,000

Decision: Expand.

Hurwicz ( a = .3):
Expand	$800,000(.3) + 500,000(.7) = $590,000
Status quo	$1,300,000(.3) 150,000(.7) = $285,000
Sell	$ 320,000(.3) + 320,000(.7) = $ 320,000

Decision: Expand.

Equal likelihood:
Expand	$800,000(.50) + 500,000(.50) = $650,000
Status quo	$1,300,000(.50) 150,000(.50) = $575,000
Sell	$320,000(.50) + 320,000(.50) = $320,000

Decision: Expand.

Step  2.

(part B): Determine Decisions with EV and EOL

Expected value:
Expand	$800,000(.70) + 500,000(.30) = $710,000
Status quo	$1,300,000(.70) 150,000(.30) = $865,000
Sell	$320,000(.70) + 320,000(.30) = $320,000

Decision: Maintain status quo.

Expected opportunity loss:
Expand	$500,000(.70) + 0(.30) = $350,000
Status quo	$0(.70) + 650,000(.30) = $195,000
Sell	$980,000(.70) + 180,000(.30) = $740,000

Decision: Maintain status quo.

Step  3.

(part C): Compute EVPI

expected value given perfect information	= 1,300,000(.70) + 500,000(.30)
	= $1,060,000

---

[Page 550]

expected value without perfect information	= $1,300,000(.70) 150,000(.30)
	= $865,000
EVPI	= $1,060,000 865,000 = $195,000

Step  4.

(part D): Develop a Decision Tree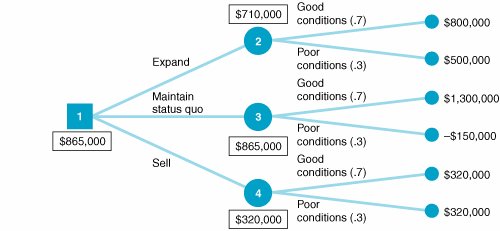

Step  5.

(part E): Determine Posterior Probabilities

---

[Page 551]

Step  6.

(part F): Perform Decision Tree Analysis with Posterior Probabilities