Management Science Modeling Techniques

[Page 16]

This text focuses primarily on two of the five steps of the management science process described in Figure 1.1model construction and solution. These are the two steps that use the management science technique. In a textbook , it is difficult to show how an unstructured real-world problem is identified and defined because the problem must be written out. However, once a problem statement has been given, we can show how a model is constructed and a solution is derived. The techniques presented in this text can be loosely classified into four categories, as shown in Figure 1.6.

Figure 1.6. Classification of management science techniques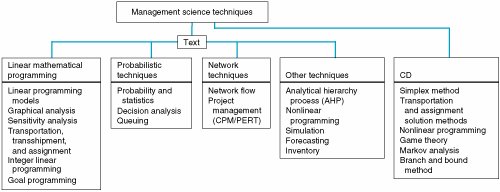

Linear Mathematical Programming Techniques

Chapters 2 through 6 and 9 present techniques that together make up linear mathematical programming . (The first example used to demonstrate model construction earlier in this chapter is a very rudimentary linear programming model.) The term programming used to identify this technique does not refer to computer programming but rather to a predetermined set of mathematical steps used to solve a problem. This particular class of techniques holds a predominant position in this text because it includes some of the more frequently used and popular techniques in management science.

In general, linear programming models help managers determine solutions (i.e., make decisions) for problems that will achieve some objective in which there are restrictions, such as limited resources or a recipe or perhaps production guidelines. For example, you could actually develop a linear programming model to help determine a breakfast menu for yourself that would meet dietary guidelines you may have set, such as number of calories , fat content, and vitamin level, while minimizing the cost of the breakfast. Manufacturing companies develop linear programming models to help decide how many units of different products they should produce to maximize their profit (or minimize their cost), given scarce resources such as capital, labor, and facilities.

Six chapters in this text are devoted to this topic because there are several variations of linear programming models that can be applied to specific types of problems. Chapter 4 is devoted entirely to describing example linear programming models for several different types of problem scenarios. Chapter 6, for example, focuses on one particular type of linear programming application for transportation, transshipment , and assignment problems. An example of a transportation problem is a manager trying to determine the lowest -cost routes to use to ship goods from several sources (such as plants or warehouses) to several destinations (such as retail stores), given that each source may have limited goods available and each destination may have limited demand for the goods. Also, Chapter 9 includes the topic of goal programming, which is a form of linear programming that addresses problems with more than one objective or goal.

---

[Page 17]

As mentioned previously in this chapter, some of the more mathematical topics in the text are included as supplementary modules on the CD that accompanies the text. Among the linear programming topics included on the CD are modules on the simplex method; the transportation, transshipment, and assignment solution methods ; and the branch and bound solution method for integer programming models. Also included on the CD are modules on nonlinear programming, game theory, and Markov analysis.

Probabilistic Techniques

Probabilistic techniques are presented in Chapters 11 through 13. These techniques are distinguished from mathematical programming techniques in that the results are probabilistic. Mathematical programming techniques assume that all parameters in the models are known with certainty . Therefore, the solution results are assumed to be known with certainty, with no probability that other solutions might exist. A technique that assumes certainty in its solution is referred to as deterministic . In contrast, the results from a probabilistic technique do contain uncertainty, with some possibility that alternative solutions might exist. In the model solution presented earlier in this chapter, the result of the first example ( x = 25 units to produce) is deterministic, whereas the result of the second example (estimating an average of 40 units sold each month) is probabilistic.

An example of a probabilistic technique is decision analysis, the subject of Chapter 12. In decision analysis it is shown how to select among several different decision alternatives, given uncertain (i.e., probabilistic) future conditions. For example, a developer may want to decide whether to build a shopping mall, build an office complex, build condominiums, or not build anything at all, given future economic conditions that might be good, fair, or poor, each with a probability of occurrence. Chapter 13, on queuing analysis, presents probabilistic techniques for analyzing waiting lines that might occur, for example, at the grocery store, at a bank, or at a movie. The results of waiting line analysis are statistical averages showing, among other things, the average number of customers in line waiting to be served or the average time a customer might have to wait for service.

Network Techniques

Networks, the topic of Chapters 7 and 8, consist of models that are represented as diagrams rather than as strictly mathematical relationships. As such, these models offer a pictorial representation of the system under analysis. These models represent either probabilistic or deterministic systems.

For example, in shortest route problems, one of the topics in Chapter 7 ("Network Flow Models"), a network diagram can be drawn to help a manager determine the shortest route among a number of different routes from a source to a destination. For example, you could use this technique to determine the shortest or quickest car route from St. Louis to Daytona Beach for a spring break vacation. In Chapter 8 ("Project Management"), a network is drawn that shows the relationships of all the tasks and activities for a project, such as building a house or developing a new computer system. This type of network can help a manager plan the best way to accomplish each of the tasks in the project so that it will take the shortest amount of time possible. You could use this type of technique to plan for a concert or an intramural volleyball tournament on your campus.

---

[Page 18]

Other Techniques

Some topics in the text are not easily categorized; they may overlap between several categories, or they may be unique. The analytical hierarchy process (AHP) in Chapter 9 is such a topic that is not easily classified. It is a mathematical technique for helping the decision maker choose between several alternative decisions, given more than one objective; however, it is not a form of linear programming, as is goal programming, the shared topic in Chapter 9, on multicriteria decision making. The structure of the mathematical models for nonlinear programming problems in Chapter 10 is similar to the linear programming problems in Chapters 2 through 6; however, the mathematical equations and functions in nonlinear programming can be nonlinear instead of linear, thus requiring the use of calculus to solve them. Simulation, the subject of Chapter 14, is probably the single most unique topic in the text. It has the capability to solve probabilistic and deterministic problems and is often the technique of last resort when no other management science technique will work. In simulation a mathematical model is constructed (typically using a computer) that replicates a real-world system under analysis, and then that simulation model is used to solve problems in the "simulated" real-world system. For example, with simulation you could build a model to simulate the traffic patterns of vehicles at a busy intersection to determine how to set the traffic light signals.

Forecasting, the subject of Chapter 15, and inventory management, in Chapter 16, are topics traditionally considered to be part of the field of operations management. However, because they are both important business functions that also rely heavily on quantitative models for their analysis, they are typically considered important topics in the study of management science as well. Both topics also include probabilistic as well as deterministic aspects. In Chapter 15 we will look at several different quantitative models that help managers predict what the future demand for products and services will look like. In general, historical sales and demand data are used to build a mathematical function or formula that can be used to estimate product demand in the future. In Chapter 16 we will look at several different quantitative models that help organizations determine how much inventory to keep on hand in order to minimize inventory costs, which can be significant.