12.3 Model of the forward LIBOR rate

Specifying the above model of the instantaneous, continuously compounded forward rate is equivalent to determining the volatility function ƒ ( t, T )(or equivalently ƒ *( t, T )). Fix some > 0, then the LIBOR rate process { L ( t, T ); t ˆˆ [0, T ], T ˆˆ [0, ]} is defined as:

Imposing a lognormal volatility structure on L ( t, T ), the associated stochastic process may be written as:

where ¼ _{L ( t, T )} is some drift function and ³ : R ² ’ R ⁿ is the deterministic, bounded and piecewise continuous relative volatility function. Letting h ( t, T )= ( ˆ« ^{T +} _T f ( t, u ) du , we make use of Ito's Lemma to determine the correct functional form of (12.6). Hence:

Here:

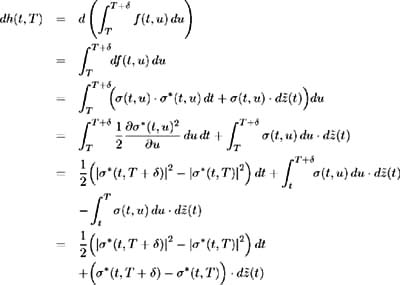
Therefore:

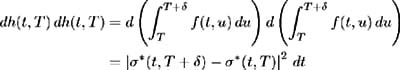
and (12.7) becomes:

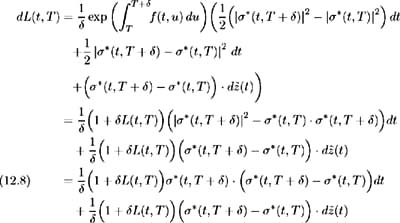
Hence by (12.6) we require:

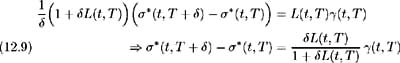
and so (12.8) may be written in terms of the ( T + )-maturity bond price volatility as:

Alternatively, solving (12.9) for ƒ *( t, T + ) we may write this LIBOR stochastic process in terms of the T -maturity bond price volatility as:

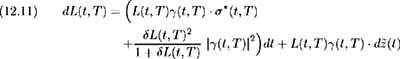
Now let us assume ^[6] ƒ *( t, T ) = 0 for all t ˆˆ ( T ˆ’ ) ˆ 0, T and T ˆˆ [0, ], then a recursive relationship may be used to define ƒ *( t, T )for T ˆ’ t ‰ as ^[7] :

Substituting this recursive relationship into (12.10), the stochastic process describing the evolution of LIBOR may be written purely in terms of LIBOR rate volatilities as:

Letting j = k ˆ’ 1 we have:

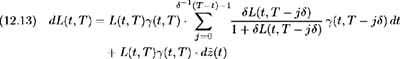
^[6] This assumption implies the volatility factor disappears for all rates where 0 ‰ T ˆ’ t < , that is the time between valuation date and maturity date is less than . This allows for the construction of a tractable model. We have ƒ *( t, t ) = 0 for all t ˆˆ [0, T ] since this is the price volatility of an instantly maturing bond. Relationship (12.9) implies:

Hence, for T = t +

since ³ ( t, t ) = 0 is the volatility of the spot LIBOR rate. So, since ƒ *( t, T )=0 for T = t and for T = t + we let ƒ *( t, T ) = 0 for all T ˆˆ ( t, t + ) as well. This is equivalent to ƒ *( t, T )=0 for t ˆˆ ( T ˆ’ , T ).

^[7] By (12.9) we have:

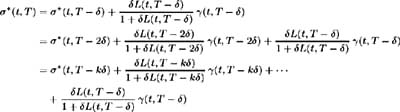
Since, by assumption, ƒ *( t, T )=0 for T ˆ’ t < the first term on the RHS vanishes for T ˆ’ t ˆ’ k < i.e. the term vanishes for k > ^{ˆ’ 1} ( T ˆ’ t ) ˆ’ 1, hence the upper bound for the summation index is k = ^{ˆ’ 1} ( T ˆ’ t ).