12.2 Initial framework
12.2 Initial framework
The mathematical framework used by BGM is much the same as that used by HJM. We have a probability space ( , { F t ; t ‰ 0}, ![]() ) where is the state space and the filtration { F t ; t ‰ 0} is the
) where is the state space and the filtration { F t ; t ‰ 0} is the ![]() - augmentation of the filtration generated by the n -dimensional Brownian motion
- augmentation of the filtration generated by the n -dimensional Brownian motion ![]() . Sincewe make use of the arbitrage-free results of the HJM analysis,
. Sincewe make use of the arbitrage-free results of the HJM analysis, ![]() is the risk-neutral probability measure with
is the risk-neutral probability measure with ![]() the corresponding Brownian motion. The trading interval is specified as [0, ] where > 0 is fixed. The following processes are defined on this probability space [4] :
the corresponding Brownian motion. The trading interval is specified as [0, ] where > 0 is fixed. The following processes are defined on this probability space [4] :
-
f ( t, T ) denotes the instantaneous, continuously compounded forward rate prevailing at time t for maturity T . The process { f ( t, T ); t ‰ T } satisfies:
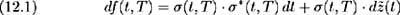
where ƒ ( t, T ) is the forward rate volatility and ƒ *( t, T )= ˆ« T t ƒ ( t, v ) dv .
P ( t, T )=exp ( ˆ’ ˆ« T t f ( t, u ) du ) describes the price evolution of a T -maturity discount bond, and so:

where ƒ *( t, T ) may be interpreted as bond price volatility and hence ƒ *( t, t ) = 0 for all t ‰ 0.
-
Defining the short- term interest rate r ( t )= f ( t, t ) for all t ‰ 0, the money market account is represented as:
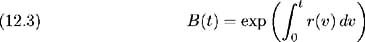
with initial condition B (0) = 1.
We know that if discounted bond prices ![]() , t ˆˆ [0, T ], T > 0 are martingales under some probability measure
, t ˆˆ [0, T ], T > 0 are martingales under some probability measure ![]() , then we are in an arbitrage-free framework. Within this framework, the bond price may be represented as [5] :
, then we are in an arbitrage-free framework. Within this framework, the bond price may be represented as [5] :
[4] he initial BGM formulation [ 9 ] of these processes uses r ( t, x ) to represent the instantaneous forward rate prevailing at time t for maturity t + x . I feel this formulation obscures any value it adds and hence I maintain consistency with the notation used in Chapter 11 by using f ( t, T ) to denote the time t instantaneous forward rate for maturity T . The obvious relationship between the two representations is r ( t, x )= f ( t, t + x ).
[5] See equation (11.28).
EAN: 2147483647
Pages: 132