Cryptography: Theory and Practice:The RSA System and Factoring | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

DEFINITION 4.1 A yes-biased Monte Carlo algorithm is a probabilistic algorithm for a decision problem in which a “yes” answer is (always) correct, but a “no” answer may be incorrect. A no-biased Monte Carlo algorithm is defined in the obvious way. We say that a yes-biased Monte Carlo algorithm has error probability equal to ∈ if, for any instance in which the answer is “yes,” the algorithm will give the (incorrect) answer “no” with probability at most ∈. (This probability is computed over all possible random choices made by the algorithm when it is run with a given input.)

The decision problem called Composites is described in Figure 4.5.

Note that an algorithm for a decision problem only has to answer “yes” or “no.” In particular, in the case of the problem Composites, we do not require the algorithm to find a factorization in the case that n is composite.

We will first describe the Solovay-Strassen algorithm, which is a yes-biased Monte Carlo algorithm for Composites with error probability 1/2. Hence, if the algorithm answers “yes,” then n is composite; conversely, if n is composite, then the algorithm answers “yes” with probability at least 1/2.

Figure 4.5 Composites

Figure 4.6 Quadratic Residues

Although the Miller-Rabin algorithm (which we will discuss later) is faster than Solovay-Strassen, we begin by looking at the Solovay-Strassen algorithm because it is easier to understand conceptually and because it involves some number-theoretic concepts that will be useful in later chapters of the book. We begin by developing some further background from number theory before describing the algorithm.

DEFINITION 4.2 Suppose p is an odd prime and x is an integer, 1 ≤ x ≤ p - 1. x is defined to be a quadratic residue modulo p if the congruence y² 𕟁 x (mod p) has a solution 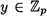. x is defined to be a quadratic non-residue modulo p if 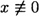(mod p) and x is not a quadratic residue modulo p.

Example 4.6

The quadratic residues modulo 11 are 1, 3, 4, 5 and 9. Note that (±1)² = 1, (±5)² = 3, (±2)² = 4, (±4)² = 5 and (±3)² = 9 (where all arithmetic is in ).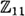

The decision problem Quadratic Residues is defined in Figure 4.6 in the obvious way.

We prove a result, known as Euler’s criterion, that will give rise to a polynomialtime deterministic algorithm for Quadratic Residues.

THEOREM 4.8 (Euler’s Criterion)

Let p be an odd prime. Then x is a quadratic residue modulo p if and only if

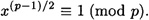
PROOF First, suppose x ≡ y² (mod p). Recall from Corollary 4.6 that if p is prime, then x^p-1 ≡ 1 (mod p) for any 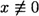(mod p). Thus we have

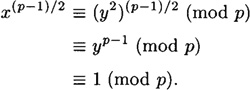
Conversely, suppose x^(p-1)/2 ≡ 1 (mod p). Let b be a primitive element modulo p. Then x ≡ bⁱ (mod p) for some i. Then we have

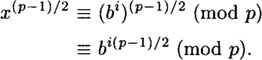
Since b has order p - 1, it must be the case that p - 1 divides i(p - 1)/2. Hence, i is even, and then the square roots of x are ±bⁱ/2.

Theorem 4.8 yields a polynomial-time algorithm for Quadratic Residues, by using the “square-and-multiply” technique for exponentiation modulo p. The complexity of the algorithm will be O((log p)³).

We now need to give some further definitions from number theory.

DEFINITION 4.3 Suppose p is an odd prime. For any integer a ≥ 0, we define the Legendre symbol 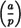as follows:

We have already seen that a^(p-1)/2 ≡ 1 (mod p) if and only if a is a quadratic residue modulo p. If a is a multiple of p, then it is clear that a^(p-1)/2 ≡ 0 (mod p). Finally, if a is a quadratic non-residue modulo p, then a^(p-1)/2 ≡ -1 (mod p) since a^p-1 ≡ 1 (mod p). Hence, we have the following result, which provides an efficient algorithm to evaluate Legendre symbols:

THEOREM 4.9

Suppose p is an odd prime. Then

Next, we define a generalization of the Legendre symbol.

DEFINITION 4.4 Suppose n is an odd positive integer, and the prime power factorization of n is . Let a ≥ 0 be an integer. The Jacobi symbol 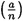is defined to be

Table of Contents